华为突破封锁,对标谷歌Dropout专利,开源自研算法Disout,多项任务表现更佳
来源:量子位
本文介绍华为诺亚实验室开源Disout算法,直接对标谷歌申请专利的Dropout算法。

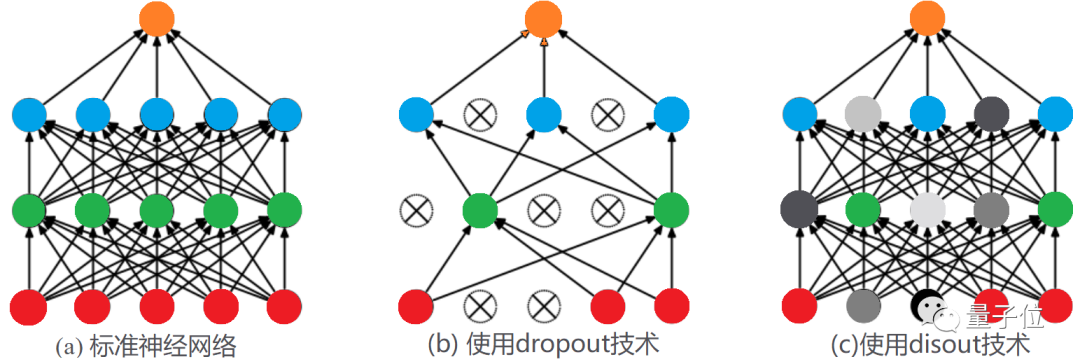
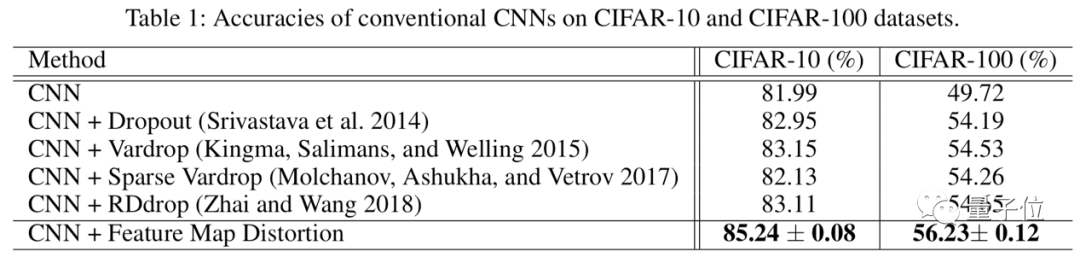

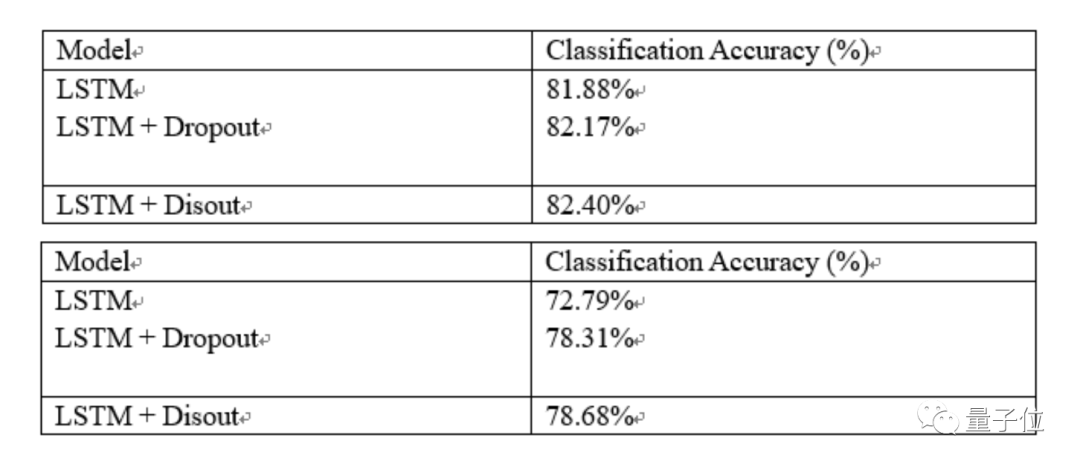
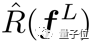 是:
是:
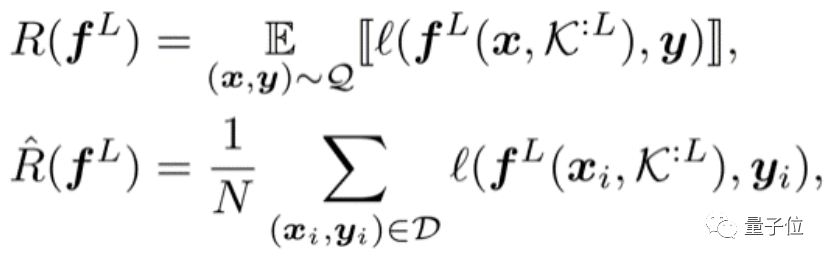
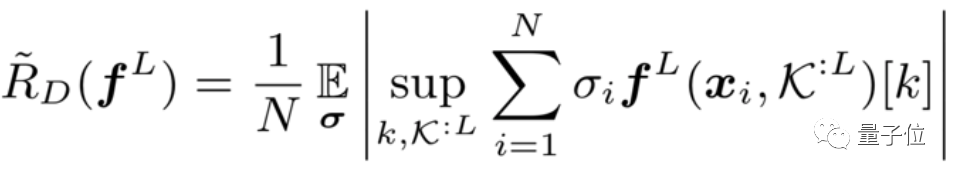
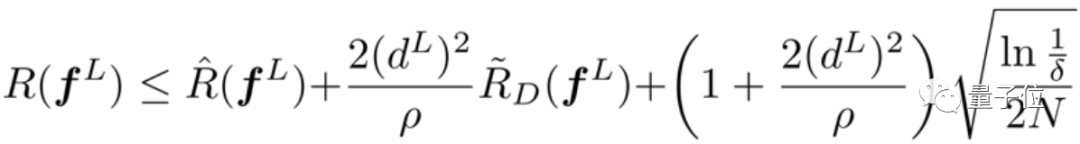
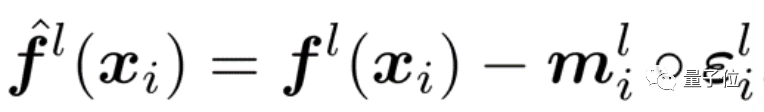


https://github.com/huawei-noah/Disout
https://www.aaai.org/Papers/AAAI/2020GB/AAAI-TangY.402.pdf
——END——



