糟糕，我学了假的微积分！

转自微信: 图灵教育, 已获授权, [遇见] 特此感谢! 

01 往事历历在目

大二那年，刚开学没多久我就度过了一个伤心的宿醉之夜，不是因为校门口最负盛名的烤冷面摊儿不见了，也不是因为我的爱豆突然宣布谈了对象，而是因为一个假期过去，我把前一年学的微积分给忘！光！了！

翻开这学期要学的《电路分析》《电磁学》《力学》，看着满篇的微积分式子，我不禁黯然神伤，捧起酒桶……

 

这是为什么呢？一转眼这么多年过去了，我有时还是忍不住琢磨：为什么微积分的保质期在我的脑子里总是这么短？

这个谜团终于在前些日子解开了——我竟然学了假的微积分。

 

02 光会算题，你知道微分的灵魂吗？

回忆一下自己学习高数的过程，我发现，我其实一直不太明白到底为什么要学微分。

学极限的时候，老师说，当 x 趋近于 0 的时候，f(x)=e^x 的极限是 1。我心想，这不就是e⁰=1 吗？还整啥极限啊，趋近于的，词儿还挺多。

学导数的时候，老师说，一个函数的导数可以反映它在几何上的变化趋势。我心想，我不求导数，直接画图也能看出它的变化趋势，为啥折腾这一遭？

学泰勒公式的时候，老师说，有了泰勒展开，我们可以求一个函数在某个点的近似值。我心想，求啥近似值啊，直接求准确值呗！

 

面对困惑的我，老师亲切地问：“孩砸，会算题了不？”

“还行，背背公式都能算对。”

“那不就得了吗？”

“可是老师，我还是觉得学微分就是自找麻烦。”

老师笑了，她说——

困扰我多年的问题，最近终于有了答案——微分的灵魂在于近似和忽略。

从小到大，提起数学，我们总是下意识地想到精确和完美。我们总觉得数学是没有商量余地的，直线就是直线，曲线就是曲线，是就是是，不是就是不是。但事实上，如果数学只容得下完美，那它就没办法成为实用的工具了。

比如，液晶显示器的像素安排是需要数学计算的。但是，如果使用数学的人执着于完美，他就会说：“我为什么要算这种东西呢？不管像素怎么安排，显示器上的画面总归是由小方块拼成的，反正不是真正的平滑画面。”

更小的方格组成与近似圆

液晶显示器显示的画面实际上是锯齿状的。但是显示器中锯齿的精细度非常高，所以我们眼中看到的就是平滑的线了。

我们也可以这样说，圆形实际上是由无数精细小方格组成的锯齿状图形，即圆是锯齿状图形的“极限”。像这样，“近似”在数学中是极好的用法。

如果执着于完美再现平滑的线，那么就不会出现液晶显示器吧。多亏了非完美主义的近似方法，才诞生了划时代的技术。

事实上，近似和忽略是一门很重要、很了不起的学问。

03 万物皆可盘，积分对象也不例外

微分的灵魂是忽略与近似，那积分的灵魂呢？当然也是忽略与近似，因为微分和积分是好基友啊！

在上大学之前，我记住了很多种图形的面积和体积公式。我理所当然地用着它们，就像使用一个一直放在厨房里的碗，但我从来不知道这个碗是从哪来的。

也许哪位先人一拍脑袋就总结出了这些公式？我也不知道自己为什么有必要了解更多。

然而，事实上，很多面积和体积公式在诞生过程中就运用了积分的思想。

面对图形中那些不一样的烟火，积分的思想就是：盘！万物皆可盘，积分对象也不例外。不管是什么东西，我们都要把它盘出规律，盘出标准，盘出智慧的光泽。

想算圆的面积吗？盘它！

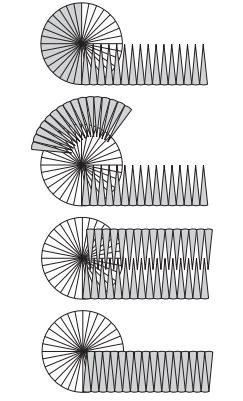
把圆展开成扇形

圆面积

☟

想算甜甜圈的体积吗？盘它！

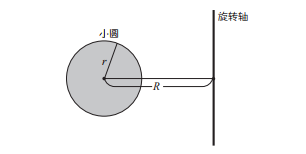
旋转圆板形成圆环体

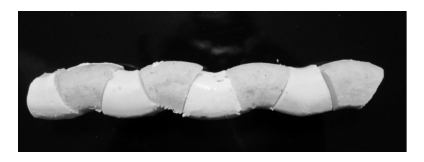
被等分的甜甜圈

重新排列被8等分的甜甜圈

甜甜圈的体积

☟

能算简单的，就能算复杂的，万变不离其宗嘛。想算地球的体积吗？盘它！

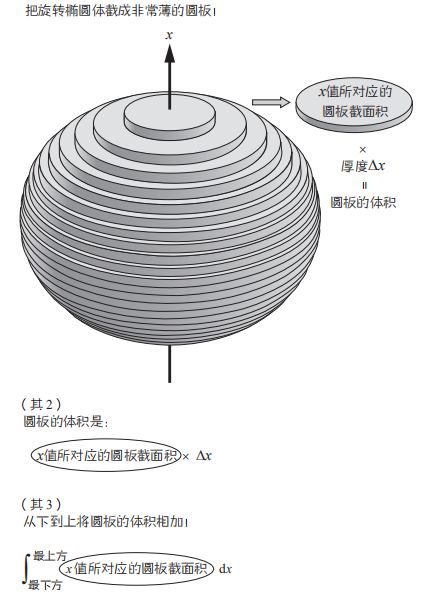
地球不是球吗？

用积分符号表示旋转椭圆体的体积

地球和边长为 10 000 km 的立方体的体积大致相等

我必须要感叹一下，如果上学的时候就知道这些，那我一定能成为班上最出色的盘……啊不，学生。

04  学了微积分不用来high，那将毫无意义

但这些都不是最重要的。我最大的发现是，只把微积分当工具，你会错过很多快乐。放下那些枯燥的习题，带着微积分的思想观察生活，你会打开新世界的大门！

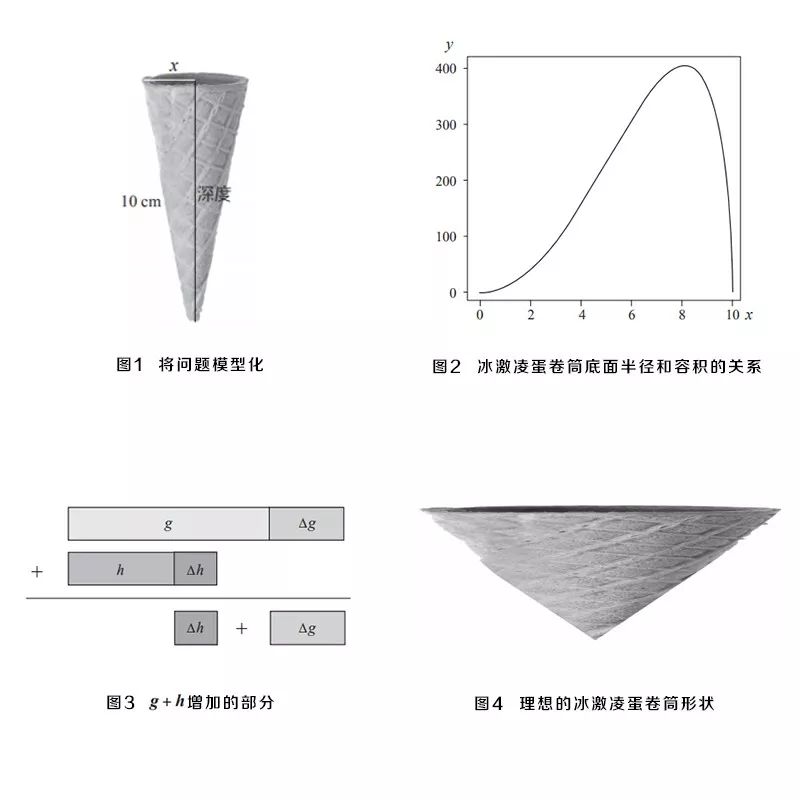
比如，你可以计算什么样的甜筒能装下最多冰激凌。

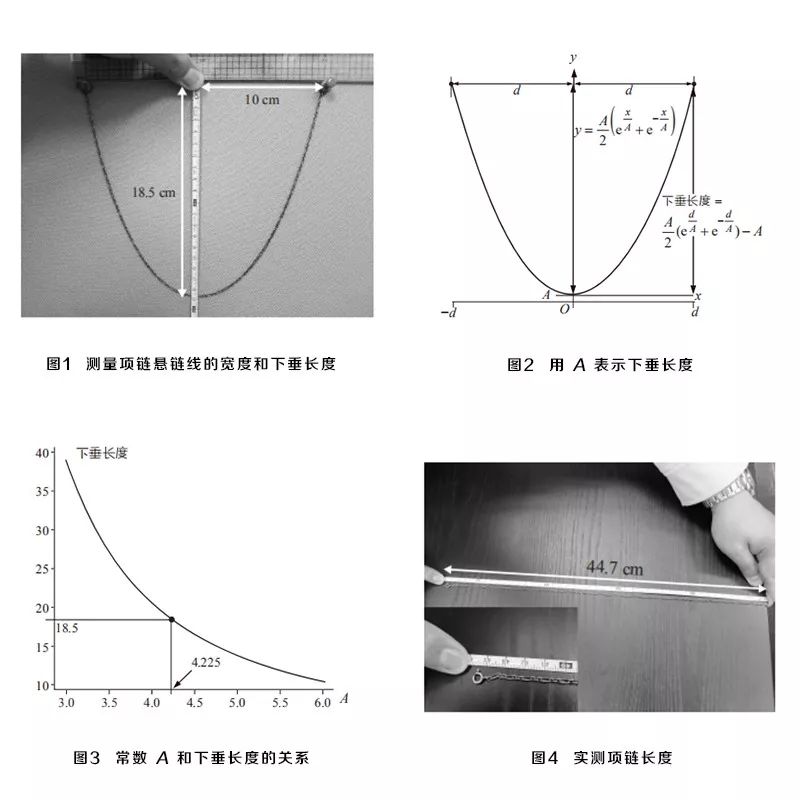
你还可以目测女神的项链有多长。

就连早餐切个鸡蛋都与众不同。

鸡蛋切割器

哇，简直让人大开眼界！

那么问题来了。这么多年过去了，我怎么就突然对微积分开窍了呢？当然是因为我找到了新世界的钥匙，也就是它！！

☟

日本最具人气的“微积分入门”读本，

仅用“阅读”便可理解微积分原理。

《简单微积分》

作者：神永正博

译者：李慧慧

微积分入门科普读物，书中以微积分的“思考方法”为核心，以生活例子通俗讲解了微积分的基本原理、公式推导以及实际应用意义，解答了微积分初学者遭遇的常见困惑。本书讲解循序渐进、生动亲切，没有烦琐计算、干涩理论，是一本只需“轻松阅读”便可以理解微积分原理的入门书。

上文中所有有趣的例子和知识点，都出自这本轻巧的小书。这本书里没有难懂的定义，没有晦涩的概念，更没有大段大段的公式推导。作者神永教授似乎并不想把课堂上的微积分教给读者，他只想让大家像认识一个朋友一样，看到微积分最朴实可爱的一面。

但谁又能说课堂上的微积分才是最好的微积分呢？和知识做朋友不是最重要的吗？

我们之所以觉得很多知识容易记住也容易忘记，说到底还是因为没有和它们成为朋友。成为朋友以后，知识当然就舍不得离开你了。( - End - )