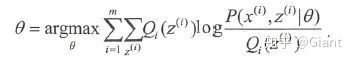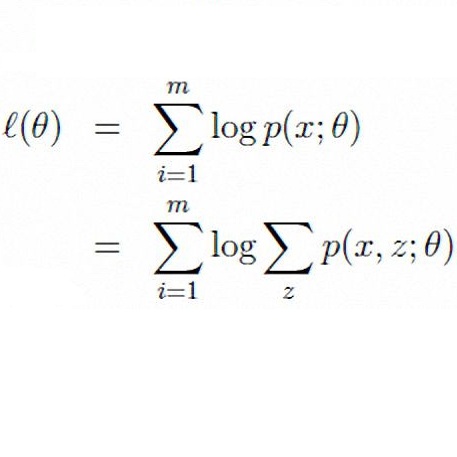KMeans聚类算法详解

原创 · 作者 | Giant

学校 | 浙江大学

研究方向 | 对话系统、text2sql

知乎专栏 | 大熊猫游乐园

---

“如果把人工智能比作一块大蛋糕，监督学习只是上面的一层奶油”。

日常生活中，从人脸识别、语音识别到搜索引擎，我们看到越来越多人工智能领域的算法逐渐走向落地。尽管全球每日新增数据量以PB或EB级别增长，但是大部分数据属于无标注甚至非结构化。所以相对于监督学习，不需要标注的无监督学习蕴含了巨大的潜力与价值。

聚类算法KMeans是无监督学习的杰出代表之一。本文是记录自己过去学习KMeans算法的系统小结，将从“KMeans简介，优缺点与优化策略，结合EM算法解释KMeans以及手推KMeans”几个方面来尽可能彻底、清晰地搞明白这个算法，希望对大家能有所帮助。

一、聚类与KMeans

与分类、序列标注等任务不同，聚类是在事先并不知道任何样本标签的情况下，通过数据之间的内在关系把样本划分为若干类别，使得同类别样本之间的相似度高，不同类别之间的样本相似度低（即增大类内聚，减少类间距）。

聚类属于非监督学习，K均值聚类是最基础常用的聚类算法。它的基本思想是，通过迭代寻找K个簇（Cluster）的一种划分方案，使得聚类结果对应的损失函数最小。其中，损失函数可以定义为各个样本距离所属簇中心点的误差平方和：

其中  代表第  个样本，  是  所属的簇，  代表簇对应的中心点，  是样本总数。

二、具体步骤

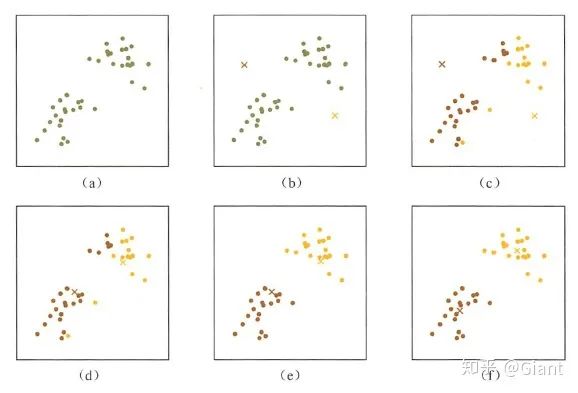
KMeans的核心目标是将给定的数据集划分成K个簇（K是超参），并给出每个样本数据对应的中心点。具体步骤非常简单，可以分为4步：

（1）数据预处理。主要是标准化、异常点过滤。

（2）随机选取K个中心，记为 

（3）定义损失函数： 

（4）令t=0,1,2,... 为迭代步数，重复如下过程知道  收敛：

（4.1）对于每一个样本  ，将其分配到距离最近的中心

（4.2）对于每一个类中心k，重新计算该类的中心

KMeans最核心的部分就是先固定中心点，调整每个样本所属的类别来减少  ；再固定每个样本的类别，调整中心点继续减小 。两个过程交替循环，  单调递减直到最（极）小值，中心点和样本划分的类别同时收敛。

KMeans迭代示意图

三、优缺点与优化方法

KMenas的优点：

• 高效可伸缩，计算复杂度 为接近于线性（N是数据量，K是聚类总数，t是迭代轮数）。

• 收敛速度快，原理相对通俗易懂，可解释性强。

KMeans也有一些明显的缺点：

• 受初始值和异常点影响，聚类结果可能不是全局最优而是局部最优。

• K是超参数，一般需要按经验选择

• 样本点只能划分到单一的类中

根据以上特点，我们可以从下面几个角度对算法做调优。

1. 数据预处理：归一化和异常点过滤

KMeans本质上是一种基于欧式距离度量的数据划分方法，均值和方差大的维度将对数据的聚类结果产生决定性影响。所以在聚类前对数据（具体的说是每一个维度的特征）做归一化和单位统一至关重要。此外，异常值会对均值计算产生较大影响，导致中心偏移，这些噪声点最好能提前过滤。

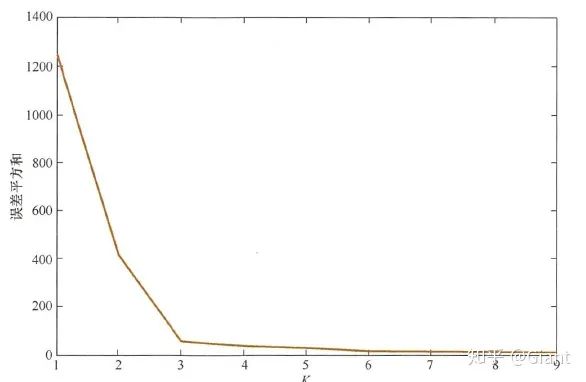
2.合理选择K值

K值的选择一般基于实验和多次实验结果。例如采用手肘法，尝试不同K值并将对应的损失函数画成折线。手肘法认为图上的拐点就是K的最佳值（上图对应K=3）。

手肘法

为了将找寻最佳K值的过程自动化，研究人员提出了Gap Statistic方法。它的有点是我们不再需要肉眼判断，只需要找到最大的Gap Statistic对应的K即可。

沿用第一节中损失函数记为  ，当分为K类时，Gap Statistic定义为：  。  是  的期望，一般由蒙特卡洛模拟产生。我们在样本所在的区域内按照均匀分布随机地产生和原始样本数一样多的随机样本，并对这个随机样本做KMeans，得到一个  ，重复多次就可以计算出  的近似值。

 的物理含义是随机样本的损失与实际样本的损失之差。Gap越大说明聚类的效果越好。一种极端情况是，随着K的变化  几乎维持一条直线保持不变。说明这些样本间没有明显的类别关系，数据分布几乎和均匀分布一致，近似随机。此时做聚类没有意义。

3.改进初始值的选择

之前我们采取随机选择K个中心的做法，可能导致不同的中心点距离很近，就需要更多的迭代次数才能收敛。如果在选择初始中心点时能让不同的中心尽可能远离，效果往往更好。这类算法中，以K-Means++算法最具影响力。

4.采用核函数

主要思想是通过一个非线性映射，将输入空间中的数据点映射到高位的特征空间中，并在新的空间进行聚类。非线性映射增加了数据点线性可分的概率（与SVM中使用核函数思想类似）对于非凸的数据分布可以达到更为准确的聚类结果。

四、从EM算法解释KMeans

EM（Expectation-Maximum）算法即期望最大化算法，是最常见的隐变量估计方法。EM算法是一种迭代优化策略，每一次迭代都分为两步：期望步（E）、极大步（M）。EM算法的提出最初是为了解决数据缺失情况下的参数估计问题，基本思想是首先根据已有的观测数据，通过极大似然估计估计出模型的参数；再根据上一步估计出的参数值估计缺失数据的值；最后根据估计出的缺失数据和原有的观测数据重新对参数值进行估计，反复迭代直到收敛。

EM算法基础和收敛有效性等问题可以参考Dempster、Laird和Rubin三人于1977年所做的文章《Maximum likelihood from incomplete data via the EM algorithm》。

KMeans算法等价于用EM算法求解以下含隐变量的最大似然问题：

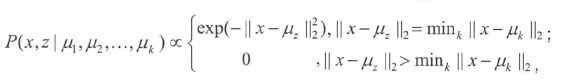
其中  是模型的隐变量，可以理解为当样本  离第  个类的中心点  距离最近是，概率正比于  ，否则为0。

在E步骤，计算：

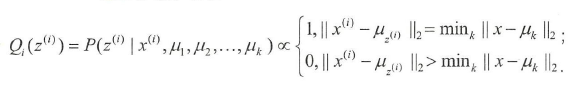
等同于在KMeans中对于每一个点  找到离当前最近的类  。

在M步骤，找到最优的参数  ，使得似然函数最大（假设  对应的分布为  ，且满足  ）：

经推导得：

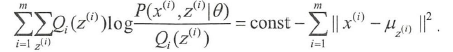
这一步等价于找到最优的中心点  ，使得损失函数  达到最小。此时每个样本  对应的类  已确定，每个类  对应的最优中心点  可以由该类所有点取平均值得到。这与KMeans算法中根据当前类的分配更新聚类中心的步骤等同。

五、手推KMeans

最后，为大家提供一个pyTorch手推实现KMeans的代码（通过sklearn包也能方便调用），结合理论梳理一遍具体实现，相信可以理解的更为扎实。

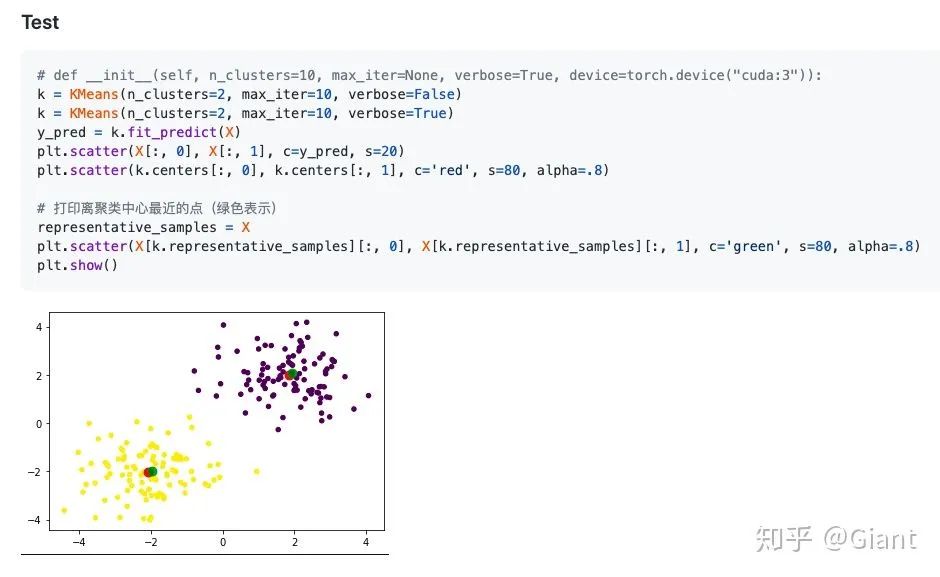
小结

KMeans作为一种无监督聚类算法，在日常生活中有大量应用。经过适当的预处理，可以对数据做初步分析，甚至挖掘出隐含的价值信息（例如对用户日志做聚类，得到一些高频高质量的新FAQ）。相比于SVM、GBDT等机器学习算法，理解起来相对通俗易懂，实乃实在又实用。

Reference：

1.《百面机器学习》5.1 K均值聚类：P92-P101

2.EM算法详解

3.手推KMeans

---

本文由作者授权AINLP原创发布于公众号平台，欢迎投稿，AI、NLP均可。原文链接，点击"阅读原文"直达：

https://zhuanlan.zhihu.com/p/184686598

欢迎加入AINLP技术交流群

进群请添加AINLP小助手微信 AINLPer（id: ainlper)，备注NLP技术交流

推荐阅读

这个NLP工具，玩得根本停不下来

从数据到模型，你可能需要1篇详实的pytorch踩坑指南

如何让Bert在finetune小数据集时更“稳”一点

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

征稿启示| 200元稿费+5000DBC（价值20个小时GPU算力）

文本自动摘要任务的“不完全”心得总结番外篇——submodular函数优化

Node2Vec 论文+代码笔记

模型压缩实践收尾篇——模型蒸馏以及其他一些技巧实践小结

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。

阅读至此了，分享、点赞、在看三选一吧🙏