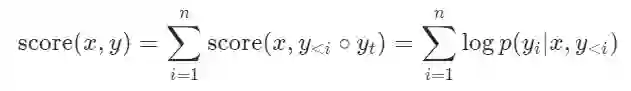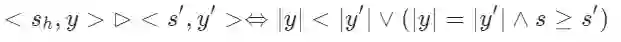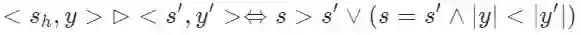Beam Search还能更快？结合优先队列的最佳优先化Beam Search

论文标题：Best-First Beam Search

论文作者：Clara Meister, Tim Vieira, Ryan Cotterell

论文链接 ： https://arxiv.org/pdf/2007.03909.pdf

---

Beam Search是当前各类文本生成任务的标配解码方式，作为一种受限的宽度优先搜索，它可以极大降低搜索复杂度。 但是，Beam Search依旧还有提高的空间！

本文提出一种结合优先队列和A*经验式搜索的Beam Search，可以显著减少调用打分函数（如负对数似然）的次数，从而能够使整个Beam Search速度大大加快，还能得到和Beam Search一样的结果。

Beam Search 概述

在文本生成中，Beam Search已经被作为一种普遍的解码方式运用在各种任务中。假设当前输入是 ，要生成的句子是 ，最大长度是 ，字典是 ，那么，所有可能的句子就是 。Beam Search就是在每一步通过打分函数只保留 个候选句子。打分函数一般是对数似然：

-最大堆，在每一步，对这 个句子中的每一个，如果它已经结束了（第5行），那么就不处理它，否则加上当前步的得分（每个句子都有 次计算得分），再把新得到的句子加入堆中，等到所有句子处理完之后，再从中取 个得分最大的。

因为Beam Search是主要的比较对象，因此我们把由Beam Search返回的 个句子叫做 -最佳集，其中的任何一个句子都称为 -最佳句子。

Beam Search 的问题

从上面的介绍讲，乍一看，Beam Search的效率很高，然而，Beam Search也隐藏着一些细节上的问题。举个例子，假设 ，词典是 ，现在保留的句子是 ，它们当前的得分分别是 ，且下一步可能的句子的得分是：

	句子	得分	句子	得分	句子	得分
acb	acba	0.30	acbb	0.31	acbc	0.25
abb	abba	0.29	abbb	0.28	abbc	0.24

看，在下一步的Beam Search中，我们当前得到的第二个句子 根本不重要，因为下一步得分最高的两个句子都来自于 ，因此，我们完全可以不去计算由 得到的三个句子。

那么，这里的关键是什么呢？是最佳优先，即让当前得分最大的句子先计算下一步，这就很像A*搜索。

A * Beam Search 

A*是一种启发式搜索，即通过预定义的得分函数，每次都首先探索得分最高的那一条路径。显然，只要得分函数定义得好，就能比DFS和BFS更快地找到正确答案。

那么在这里，所谓的正确答案就是BS得到的 -最佳结果。我们的目标是设计一种启发式的搜索算法，既能得到 -最佳结果，又比BS更快。

下面的算法就描述了一种通用的搜索算法框架。

注意观察，和BS相比，该算法引入了4个关键的成分：（1）比较符；（2）停止策略；（3） ；（4）经验函数。其中除了（3）是BS原有的之外，其他的都是新增的。有了这几个成分，就可以使用该算法实现BS，和即将要介绍的A* Beam Search。

来看一下这个算法做了什么。首先用定义了一个优先队列；然后在搜索的每一步，直接看得分最大的那个句子，如果这个句子结束了，那么就继续放入优先队列中。

否则像BS一样考虑字典中的每个字，在原来的得分（如对数似然）上再加上经验函数得分，然后再把它送到优先队列中。

注意到图中绿色的部分，它的意思是，对同一个句子长度，如果之前已经遇到了 个同样长度的句子，那么后面的同样长度的句子就不再考虑了，这是因为最先考虑的一定是得分最大的，后面打分的得分过小再考虑就没有意义。

那么这个算法怎么恢复到BS呢？其实很简单，只需要让（4）经验函数恒为0，让比较运算符（1）为：

这个式子的意思是，让那些要么长度更短要么长度相同且得分更大的句子优先被计算，这其实和BS是一致的。因为BS在每一步要么优先考虑已经结束的句子，要么长度相同但得分更大。

同时让终止条件（2）为：

也就是说要让所有句子都搜索完。

那么，怎么用这个算法实现最佳优先的A* Beam Search呢？回想一下，A*是优先探索得分较大的路径，但是它并不限制路径的长度，也就是说，如果已经探索了 条长度为 的路径，如果后面需要，它还会继续探索长度为 的其他路径。

所以它在最坏情况下仍然是 的。将A*和BS结合起来，就是要在A*算法上限制可探索的路径数，这就是上述算法的思想。

所以，最佳优先搜索就可以定义为：

• （1）比较运算符：
• （2）终止条件：
• （4）经验函数：根据得分函数的设置（对数似然设置为0）

正如上面所述，这个算法的优势在于，对于对数似然而言，一旦已经计算了长度为 的 个句子，那么后面任何长度小于 的句子都不需要再考虑了，因为它们的得分在该长度上一定更低。

本文有一节专门证明了该结论，并证明了该算法的时间复杂度，由于内容较为复杂，有兴趣的读者可以参考原文Section 4。

下图是从本算法可以导出的主要搜索算法，包括BS，最佳优先BS，A* 等算法。可以看到，通过定义4个关键因子，我们可以实现各种典型的搜索算法，当然运用在文本生成上，BS、最佳BS和A* BS是我们最关心的。

实验

空口无凭，且看实验效果。本文在多个数据集上测量各搜索算法具体调用了多少次得分函数。注意到这里没直接比较运行时间，原文认为运行时间和硬件关系很大。

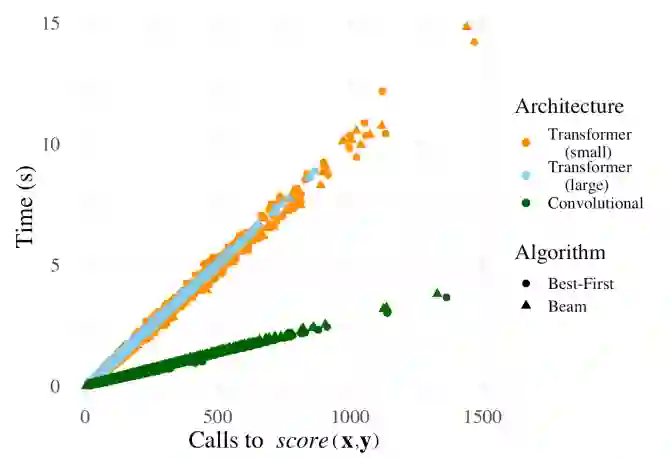
下图是在本文实验的机器上，运行时间和得分函数调用次数的关系。可以看到，二者有很强的线性相关性，所以直接比较得分函数是合理的。

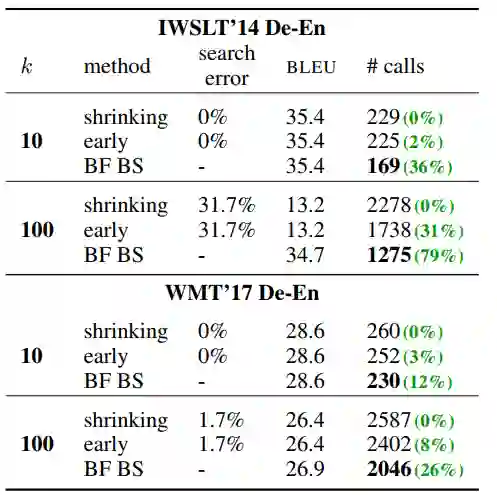
下表是主要实验结果。Beam Search (ES)是指使用了提前终止的BS。

从结果可以看到，相比BS和BS(ES)，BFBS调用得分函数的次数显著降低，这在 很大的时候尤其明显。这也就意味着，模型花在解码上的时候大大缩短。

下面一个问题是，BFBS真的可以取得BS的最后得到的句子吗？如下表所见，shrinking和ES都不能完全得到BS的结果（ ），反而效果也会变差。

相反，BFBS始终能得到BS一样的结果，只要BS能够取得好效果，BFBS也就能取得同样的效果。

上面的实验都是基于对数似然这个得分函数而言，对于其他得分函数，如互信息、长度归一化等，本文也都做了实验，限于篇幅，在此不再展开，有兴趣的读者可以参考原文。

小结

这是一篇偏算法理论的应用文，提出了一种通用的Beam Search算法框架，采用不同的比较运算符、经验函数、终止策略或Beam Size，算法可以复原很多常见的搜索算法。

基于这个算法框架，本文提出了一种新的，基于最佳优先策略的Beam Search，和BS相比，能够显著减少得分函数的调用次数，从而提高解码速度。

当然，本文所提出的算法其实并不算简单，在理解上也有诸多障碍，尤其是很多细节，如是否可以并行化解码，优先队列又该怎么在并行条件下实现等，都需要仔细推敲。原文Section3.1给出了实现的概述，读者可以根据此自己尝试实现一个版本。

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。