春节充电系列：李宏毅2017机器学习课程学习笔记03之梯度下降

【导读】我们在上一节的内容中已经为大家介绍了台大李宏毅老师的机器学习课程的regression问题，其中简要提及了梯度下降（gradient descent），这一节将主要针对梯度下降问题展开分析。本文内容涉及机器学习中梯度下降的若干主要问题：调整学习率、随机梯度下降、feature scaling、以及如何直观的理解梯度下降。话不多说，让我们一起学习这些内容吧。

春节充电系列：李宏毅2017机器学习课程学习笔记01之简介

春节充电系列：李宏毅2017机器学习课程学习笔记02之Regression

课件网址：

http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML17_2.html

视频网址：

https://www.bilibili.com/video/av15889450/index_1.html

李宏毅机器学习笔记—Gradient descent

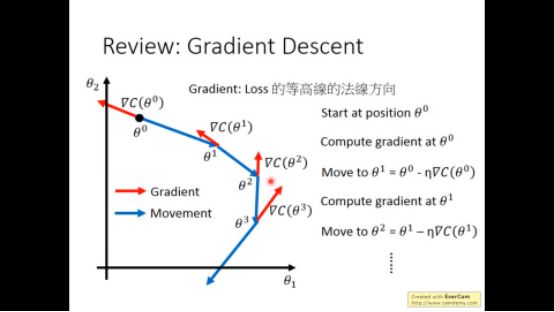
在上一次的笔记中，在regression我们已经略微讲述了gradient descent（梯度下降），现在回顾一下

现在我们具体讲述一下gradient descent里面的问题

▌1. tuning your learning rates

---

---

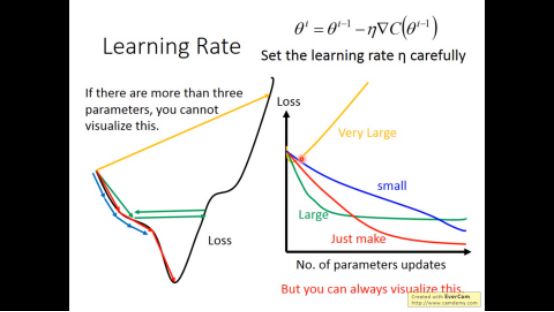
在gradient descent过程中，learning rate需要我们自己设置，当其太小时，training过程太慢了，太大时，可能在最低点左右跳跃，当设置的恰恰好时，训练才会正常进行。去下图所示

在最开始的时候，我们离最低点远，采用较大的学习速率比较好，当离最低点越来越接近时，采用较小的学习速率可能比较好。所以固定的learning rate可能不太好，我们可以采用自适应的学习速率。

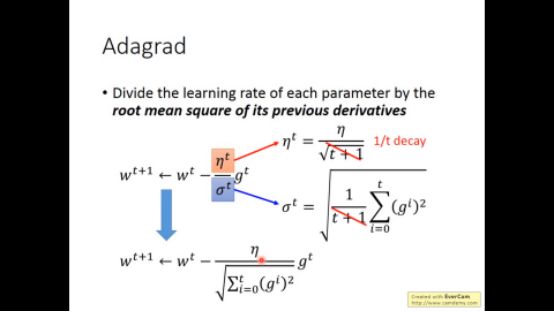
下面介绍一个称为adagrad的方法

从上图可以看出，随着训练次数的增加，训练速率越来越慢，且学习速率和以前的微分有关。

我们可以对这个方法一个直观的解释：这个方法可以强调训练速率的反差有多大

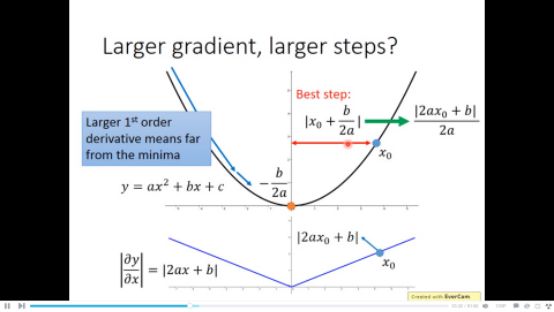
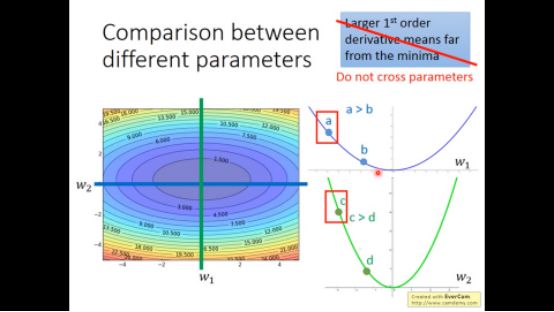
再来看看实际的解释，在一元函数中，一阶微分大小和离最低点距离成正比

但在多元函数中不是这样的，比如a和c

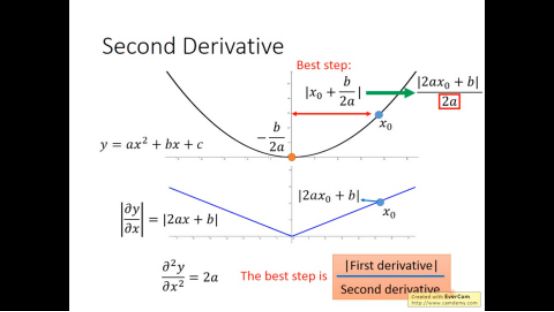
实际上继续观察下图，到最低点的距离不仅和一阶微分有关，还和二阶微分有关，C虽然一阶微分大，但二阶微分也大

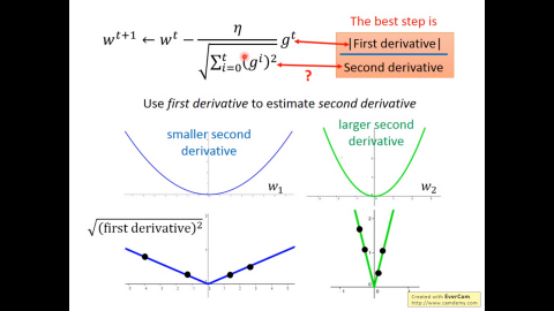
所以adagrad中分母项相当于用来估计二次微分，直接算二次微分增大计算量，于是用一次微分来估计，采样许多一次微分点，二次微分大的地方在相同位置自然比二次微分小的地方平方大。

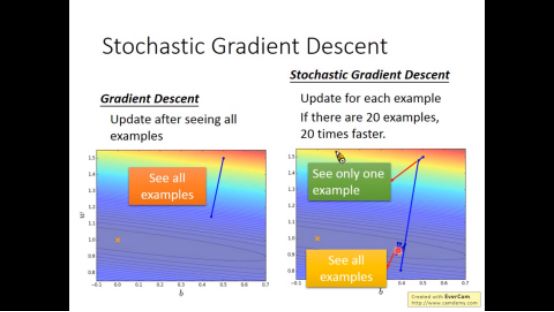
▌2. 随机梯度下降（stochastic gradient descent）

---

---

之前是算所有data的loss ,现在随机采样一个点，算这个采样点的loss，然后梯度下降

用这种方法速度更快，但以前的方法更平稳

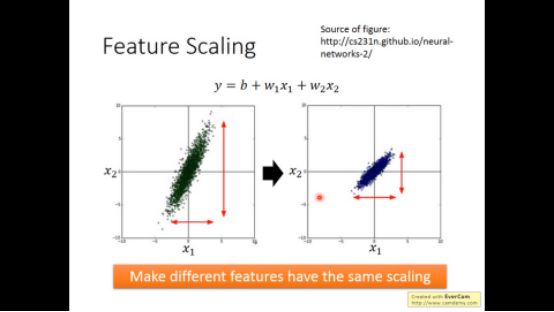
▌3. Feature scaling

---

---

X的不同特征可能scale不一样，feature scaling的方法是让不同的feature用同样的scale

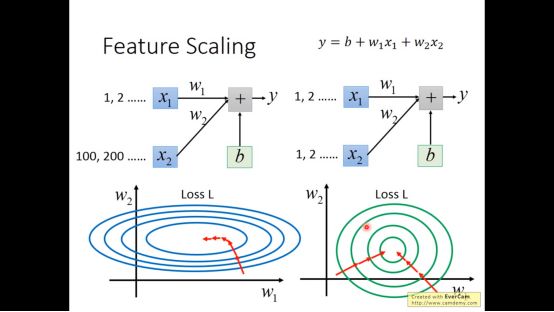
下图左边虽然也是梯度下降，但没指向最低点

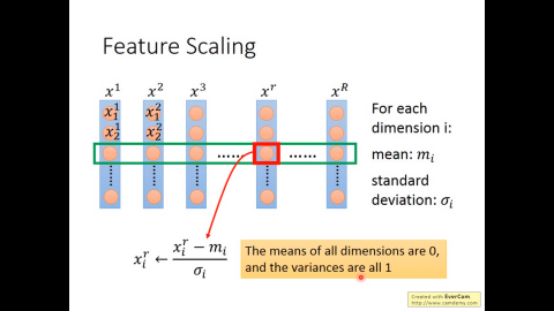
Feature scaling的方法很简单，如下图所示

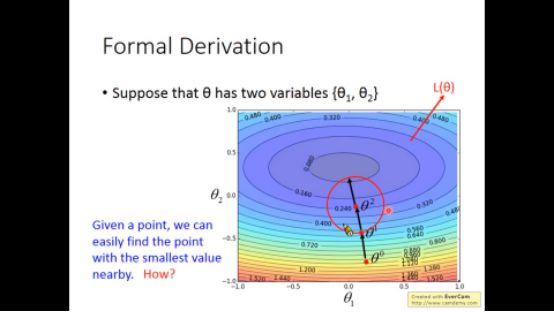
▌4. 从另一个角度来看待梯度下降方法

---

---

给定一个点，我们很容易找到其周围的最小点

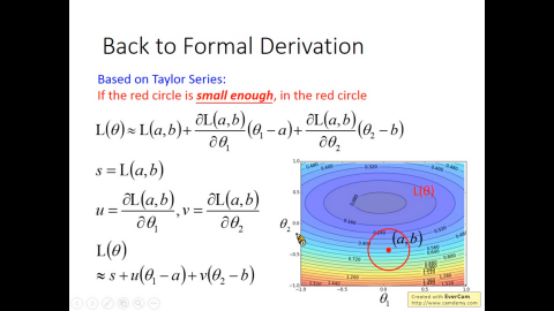
先对在此点附近进行泰勒级数展开

然后h函数在此点周围可以近似表示如下形式

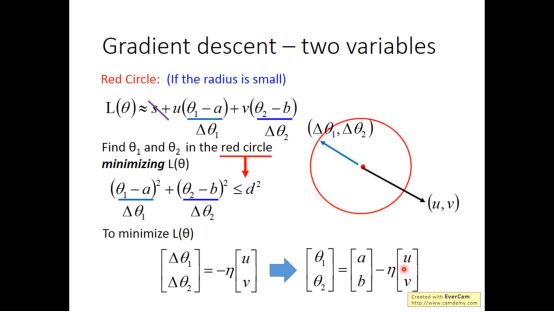
当u，v看做向量时，让loss最小时，如下图所示，要求反向即可

进而我们可以得到梯度下降的表达式

请关注专知公众号（扫一扫最下面专知二维码，或者点击上方蓝色专知），

• 后台回复“LHY2017” 就可以获取 2017年李宏毅中文机器学习课程下载链接~

-END-

专 · 知

人工智能领域主题知识资料查看获取：【专知荟萃】人工智能领域26个主题知识资料全集（入门/进阶/论文/综述/视频/专家等）

同时欢迎各位用户进行专知投稿，详情请点击：

【诚邀】专知诚挚邀请各位专业者加入AI创作者计划！了解使用专知！

请PC登录www.zhuanzhi.ai或者点击阅读原文，注册登录专知，获取更多AI知识资料！

请扫一扫如下二维码关注我们的公众号，获取人工智能的专业知识！

请加专知小助手微信（Rancho_Fang），加入专知主题人工智能群交流！

点击“阅读原文”，使用专知！