为什么琴键要排成等比数列?
钢琴的每个键频率是多少?频率的排列有什么关系?黑白键的排列方式是出于什么原因?为什么有的音合在一起会和谐共处,有的音和在一起会打架?后来发现数学其实可以解释这些问题。
下面的话可能不严格,但是音乐不需要严格,我们只需要列出想要满足的条件,然后在这些条件下找到一个极优解,问题就算解决了。
一、频率排列和琴键排列
说钢琴一共有88个键,它们各自的频率组成一个等比数列,比例系数是2开12次方,即2^(1/12),中音A(左起第49个键)的频率规定为440Hz,于是所有88个键的频率都确定了。
现在就有一个问题,为什么是等比数列而不是等差数列?从“十二平均律”这个名字看,在最低频率和最高频率之间均匀分布88个音,也应该得到一个等差数列才对。
这里有两个原因。第一个原因,也就是我觉得最重要的原因,是取决于人的听觉。人耳分辨两个音的高低,靠的是两个音之间的频率比例,而不是频率差值。比如说,一个正常人可以清楚的区分50Hz和55Hz,但却很难区分5000Hz和5005Hz(也许莫扎特可以,但是莫扎特是大神,大神是不具备参考意义的…)。这就意味着,如果钢琴上音的分布是等差数列,那么越到高音,你就会发现两个音越难以区分。这不是我们想要的。
当然这不能决定琴键必须是等比数列,因为如果你听到两个音不太好区分,那么只要增大它们的频率差即可,也就是说,耳朵的限制只能导致越到高音区,频率差越大而已。但是从数学的角度,我们可以证明这些音的分布必须是等比数列。这也就是我认为的第二个原因。
我们希望琴键的排列具有周期性,这样以便钢琴家找到每一个音的位置。最方便的获取周期的方式就是:一巴掌忽上去,就是一个最小正周期----这是手感上的周期性。我们要确定这一巴掌里面能覆盖多少个键:太少了不行----因为这样就限制了钢琴音乐的丰富性;太多了也不行----因为这样会导致每个键的宽度很窄,容易一指头戳到两个键。就现有钢琴的排键密度,好多胖纸也会吐槽按不到两个黑键中间去,巴赫这货貌似就挺胖的…于是巴赫就想,一巴掌里面排12个音很恰当,7个白键,5个黑键,黑键以两个一组、三个一组,间隔排列在均匀分布的白键之间。这是一个很好的排列方式:这使得你一巴掌无论拍在什么位置上,都会拍到一个最小正周期,并且具有视觉上的周期性----钢琴家很容易一眼就确定每个音的位置。要满足音的数量不多不少以及两个周期性要求,这是最好的排列方式了。
我们还希望一巴掌上去,大拇指和小拇指的两个音应该在相邻两个周期中的相同位置,比如说…(1234567)(1234567)(123…,一巴掌上去,大拇指和小拇指正好按到相邻的两个1、两个2等等。这两个音要非常和谐的共存,简单地说就是听起来超爽~
(从下面开始,用粗体的形如Ab来表示A_b,即A下标b)
我们现在知道声音是周期性振动,音色取决于波形。钢琴声音的波形不是sin,因此用f(wt)表示角频率为w的琴键的波形,那么两个音一起按下去的效果就是F(t)=f(w1t)+f(w2t),(不妨设w2>w1)。我们希望F(t)的周期尽可能短(这里的“周期”指的是波形函数的数学周期,并不是人耳的听感周期,人听到的感觉是两个独立的频率),一个周期内的波形尽可能简单。简单起见,设f(t)的最小正周期是1,F(t)的最小正周期是T,那么F(T)=f(w1T)+f(w2T),其中w1T=i,w2T=j,i和j都是正整数,那么T=i/w1=j/w2要尽量小,也就是说i=(w1/w2)j,我们要使i和j都尽量小。最佳的方式就是w2=2w1,这时i=1,j=2,这是最优解了。
我们称上述这两个音为一个“八度”,因为一个周期内有7个白键,如果标记为1234567的话,这两个键就对应1和8。上述结果表明,一个八度的频率应该是二倍关系,你一巴掌上去,总归是按到频率比例为1:2的两个音。
现在我们还有一个想法,就是如果我按下两个键,只要它们的间隔相同,那么无论这两个键是在什么位置上,除了频率高低以外,它们合成的效果都应该相同(这说法有种“一致连续”的赶脚)。从数学的角度讲,也就是说:F1(t)=f(wit)+f(wjt),F2(t)=f(wmt)+f(wnt),如果j-i=n-m>0,那么存在a>0,使得F1(at)=F2(t)。简单地说,就是我可以通过横轴缩放,使得F1(t)与F2(t)重合。
F1(at)=f(awit)+f(awjt)=F2(t)=f(wmt)+f(wnt),于是awi=wm且awj=wn,两式相除得到wj/wi=wn/wm。令j-i=n-m=1,这就意味着w(i+1)/wi=w(m+1)/wm=Constant对任意的i和m成立,这就证明了琴键频率必须排成等比数列。
最后需要确定的是这个数列的比例系数。一个八度的频率比例为1:2,中间有11个音,12个间隔,因此比例系数是2^(1/12)。
至于为什么中音A的频率是440Hz,这完全是出于规定。这样一来,所有的A音频率都是整数(除了最低音27.5Hz),其余的音频率全是无理数(当然实际调音的时候,只要差不多就行了……)。钢琴上最低音频率为27.5Hz,最高音频率约为4186Hz。
二、听感周期与大小调
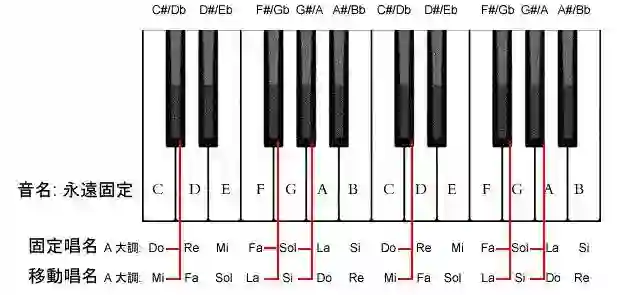
这里还有第三个周期性----听感上的周期性。首先来一张琴键图:
上面这张琴键图,Do、Re、Mi、。。。、Si、Do,分别对应CDEFGABC。以#代表升,b代表降,那么一个周期内的5个黑键依次称为#C、#D、#F、#G、#A或bD、bE、bG、bA、bB。
我们说,两个相邻琴键的间隔称为半音,比如C5和#C5、E5和F5、bA5和A5;中间隔一个琴键则称为全音,比如C5和D5、#F5和#G5、E5和#F5。
以大调为例。C大调是以C作为Do,然后取间隔为“全,全,半,全,全,全,半”,依次确定Re、Mi、。。。、Si、Do。这些音全部在白键上。
当然也可以随便找一个音定义为Do,然后按照上面所说的间隔确定相应的Re、Mi、……、Si、Do,这也构成一个大调。如果你选了图中的D定义为Do,那么按照上面的规则构造出的就是D大调;如果你选了bE5作为Do,那么就造出了降E大调(至于为什么不叫升D大调,那是因为这个大调的音阶里面有D出现,但是没有E出现,E被替换为bE,而D还是D,没有被替换为#D)。除了C大调以外的所有大调中都会出现黑键。
听感上的周期性就在于两点:1) 任何两个大调,除了频率整体的不同以外,给人带来的听感是完全相同的。也就是说如果你没有绝对音高能力(就是我随便给你弹一个音,你就能听出来它是哪个键),那么我冷不丁给你来个C大调,然后过段时间再给你来个E大调,你就完全不能区分出它们的不同…2) 如果你弹C大调,从某个很低的Do开始往上弹,那么你的听感就是(DoReMiFaSoLaSi)(DoReMiFaSoLaSi)…的循环,当然频率会越来越高,但是除整体频率变化之外,每个周期内音和音之间的联系感是完全相同的。
当然还有小调,它们的间隔规则是“全,半,全,全,半,全+半,半”。例如a小调,是A B C D E F #G A。小调的效果就是比较忧郁比较冷,很容易听出它和大调的区别。但是如果你没有绝对音高能力,那么不同的小调在你听来就是相同的(如果你听到两个小调的间隔时间够长的话)…
一言以蔽之,就是说两个频率数列{ai}和{bi},你能否听出它们的区别,取决于{ai/bi}是不是常数列。你会认为A大调和B大调、或者a小调与b小调是相同的,因为{Ai/Bi}和{ai/bi}都是常数列;但你很容易区分(DoReMiFaSoLaSi)和(FaSoLaSiDoReMi)的区别,因为它们相除不是常数列。琴键排列的最小正周期导致你必须等到下一组(DoReMiFaSoLaSi),才会有相同的听感,之前的任意一组7个白键,听感都是互不相同的。
作曲家喜欢用转调,比如一首曲子,本来是A大调,中间转成了E大调直到结尾,如果两段的旋律相同,那作曲家和音乐家会听出这两段不一样,但一般人会觉得这两段就是在重复。也许在转调的过程中,你能听出一些变化来,但是转完以后,你就分不清前后的区别了,比如kiss the rain最后一段,转调的瞬间会让你听起来别扭,但是转完了以后,你会觉得旋律和之前就是一样的;再比如《月光》第三乐章,听起来像是重复了3遍,前两次确实是全同的重复,但是第三次,它就已经不在同一个调上了。更巧妙的曲子,旋律类似,但是音的间隔有微调(相当于一个数列的大小关系不变,但是间距有变化,效果类似于大调转小调),如果两个旋律前后隔得够远,一般人也有可能听不出区别来,贝多芬经常干这种事情,比如的《悲怆》和《黎明》的第一乐章。
三、和谐与不和谐
前面提到过,听感取决于波形。如果波形简单,周期性好,那么听起来就爽;反之就不爽…为了看到波形效果,我们现在假设钢琴单音的波形就是sin,这样几何画板就能画出来了。
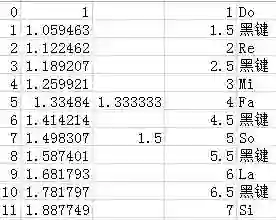
上述表格第二列是2^(i/12),第三列是第二列的有理数近似值,第四列是我标记音高的方式,第五列是对应的音。
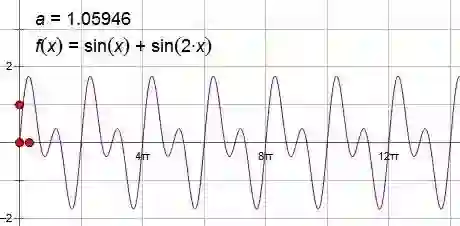
最和谐的当然是八度两个音了,它们的频率关系是二倍,波形如下:
看起来很爽,所以听起来也一样。正是因为要这么爽,所以它决定了八度频率的二倍关系。
再看一个和谐的例子。在表中可以看出So和Do的频率关系约是1.5倍,可以猜测如果Do+So+Do,即1+5+8这三个音一起按下去,应该会很和谐。波形如下:
看上去确实很和谐,如果不相信的话,可以去钢琴上弹一下,确实听起来很爽。
同理,Do+Fa+Do也应该很漂亮:
大三和弦是Do+Mi+So,即1+3+5,这是一个协和和弦,可以看到波形如下:
虽然没有前三张漂亮,但是对耳朵而言,这样还算是很有规律的…
小三和弦是1+2.5+5,这个和弦就不如大三和弦那么舒服了,波形如下:
确实是有点乱,不过听起来还算是可以。下面随便找一个听上去就蛋疼的组合,1+1.5+3+4,波形如下:
我看这个波形就觉得它很蛋疼,甚至还有拍频的影子。也许你会觉得它看上去没比小三和弦烂多少,但是如果你看到它后面的样子:
你最好拿它去和Do+So+Do的波形比一下……
当然以上只是数学的一种解释,漂亮的波形确实能产生好听的声音,但是蛋疼的波形不一定就会难听。不同的音组合会给人不同的感受,就好像小调带来忧郁抒情的氛围,月光、辛德勒名单、肖邦夜曲第一首,(还有我军训时写给14连的那首煞风景的无词歌),这些都是用小调写的,但如果你把小调的和弦画成波形,那必须是很蛋疼的样子…作曲的时候用哪些音,取决于作曲家的听感。至于为什么不同的音乐(无非就是各种频率和音色的音按某些规律组合)给人带来的感受不一样,那就不清楚了…
四、中国风音乐转变为日本风
这是很多人感兴趣的问题。我们大中华的音乐,通常用大调写成,听起来雄伟大气上档次;而小日本的音乐通常用小调写成,听起来阴郁狭窄甚至不乏蛋蛋的忧伤。但是如何把音乐转变成日本风格呢?
其实说白了就是把一首大调音乐,转换成起音相同的小调。比如有一首C大调的曲子,它对应的音阶是C D E F G A B C,你应该把它转换成c小调,对应的音阶是C D bE F G bA B C。你需要做的是把这首曲子里面所有的E和A降半音,变成bE和bA,其它音保持不变。如果是G大调,那就转成g小调,把所有的E和B降半音变成bE和bB。其它大调也类似,只不过你要小心的判断要降的是哪两个音。
不同的曲子在这种变换下会呈现出不同的性质。有的曲子,改完以后立刻节操尽失,变得极其小日本,我称这一类曲子为“可日的”,或者“Fuckable”,典型的例子有《翻身的日子》、《牧童短笛》、《浏阳河》等;有的曲子,改完以后旋律变得很怪,但是丝毫没有日本风,甚至还能保留原来雄壮亦或是大气的风格,颇有“宁为玉碎不为瓦全”的气节,我称这一类曲子为“不可日的”,或者“Unfuckable”,典型的例子是舒伯特的《军队进行曲》;还有的曲子改完以后,旋律很奇妙,时而有淡淡的日本风,时而又全无,时而抒情,时而蛋疼,这种既想hold住节操却又心有余而力不足的曲子,我称之为“半可日的”,或者“Semi-Fuckable”,典型的例子是《彩云追月》,这首改完以后更多的表现出格里格的范儿,以及诡异的没有前后联系感的旋律。
五、关于傅里叶
有人表示前面说的和谐不和谐,其实就是傅里叶变换。我觉得对这个问题用不上傅里叶。因为:
1. 傅里叶级数里的基函数是sin和cos,它们对于倍频有正交性和完备性。但是钢琴键的单音波形不是sin,之前设它为f(wt),它对于不同的w就不一定有正交性和完备性了,我情愿赌它根本没有正交完备性……如果把每个单音f(wt)都以{sin(nwt), cos(mwt)}为基进行分解,那也没有什么意义,因为我们听到的直接就是频率为w的f(wt)波形,而不是分解出来的AnSin(nwt)和BmCos(mwt)。
2. 如果你说把几个音合成以后的波形再做分解,比如Do+So+Do的那个波形,那就更没意思了。因为除了像八度这种倍频关系的音组合以外,其它的音频率关系都是无理数,这就意味着严格来说它们合成的波形是没有周期性的。前面所说的“波形周期性好”只不过是说你一眼看上去的效果而已,看起来很有规律。对一个没有周期性的定义域无穷的函数不能做傅里叶级数分解,而只能做傅里叶变换,这时搞出来的系数就不是离散的值,而是一个连续谱。
3. 就算你把波形做了近似,比如把Do+So+Do近似为F(t)=f(t)+f(1.5t)+f(2t),当然这个F(t)是有严格周期的,然后你把它给傅里叶分解了,搞出一堆系数,那也没什么用。因为我弹琴的时候完全可以给这三个音任意的不同的力度,这会让所有的系数全变掉,你一定会蛋碎的……你不近似直接做傅里叶变换也一样,Φ(k)会整个变掉。
这篇文章想表达的理由是:如果几个音的频率关系可以约成分母很小的分数,那么它们合成的波形就会体现出很好的视觉上的周期性,那么听起来就会和谐。在乐理里面也是类似于这么说的,你可以百度百科或维基百科一下“和弦”。
最后,就像开头说的,“音乐不需要严格”,我觉得何必要用傅里叶这种大杀器来解决音乐这种小问题呢……没有数学,音乐照样好听;有了数学,音乐也不会因此更好听。何况数学比音乐要傲娇的多了,难道你有听说过“音乐虐我千百遍”这种说法吗?音乐能在数学虐死我的时候把我治愈,那就足够了......
∑编辑 | Gemini
文章内容来自网络,感谢原作者!
算法数学之美微信公众号欢迎赐稿
稿件涉及数学、物理、算法、计算机、编程等相关领域
稿件一经采用,我们将奉上稿酬。
投稿邮箱:math_alg@163.com