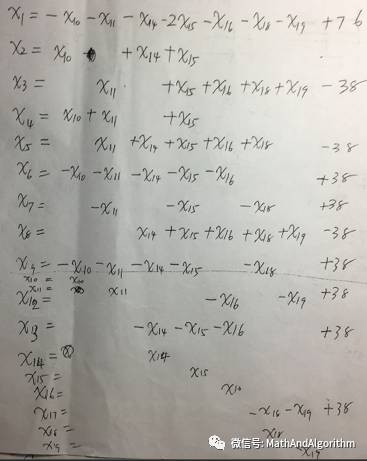幻方的故事与求解

2017 年 10 月 14 日 算法与数学之美 黄岛主的世界

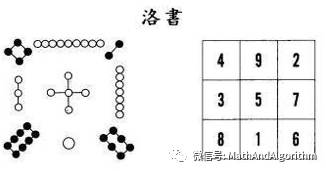
《射雕英雄传》里面有一个情节，郭靖带着受伤的黄蓉四处求高人疗伤，遇见瑛姑。瑛姑也爱好各种奇门术数，但是花了好多年却解不出一个三阶幻方。这个三阶幻方也就是“洛书”，它有三行三列，九个空格分别填上一到九这九个数字，使得每行、每列、每条对角线上三个数的和都相等。

黄蓉是黄老邪的女儿，古灵精怪，自然也精通此道，很快告诉了瑛姑答案。于是瑛姑就告诉郭靖黄蓉可以找段皇爷疗伤。当然瑛姑其实也是为了找段皇爷寻仇。这是后话。其实三阶的幻方太简单了。我倒觉得金庸可以可以把这一段情节改成瑛姑解的是一个五阶幻方，就是五行五列的幻方，甚至是七行七列的幻方，这样花十几年解不出也情有可原，难度大些，瑛姑也不至于显得那么笨。不知道金庸是不是为了衬托黄蓉的聪明？

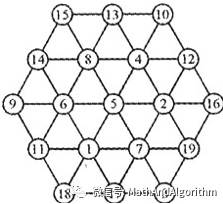
瑛姑只是在幻方上花了十几年而已。接下来主要要讨论一个六角幻方，也称幻六边形，却花费了一个人前后52年的时间！用尽一生的心血就为解一个幻方。无论如何这种精神很让人钦佩，毕竟那是一个计算机还没有普及的年代。

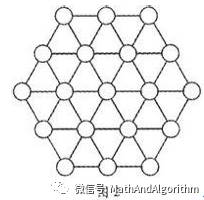
一百年前的1910年，一位叫阿当斯的青年人，对六角幻方产生了浓厚兴趣。他趁着在铁路公司阅览室当职员之便，利用一些空闲时间，去摆弄从1到19这19个数。冬去春来，度过了漫长的47个年头。经过了无数次的挫折、失败，使他由一个英俊少年，变成了白发苍苍的老头，但是他仍然不甘心失败，这就是兴趣的魔力。

1957年的一天，病中的阿当斯，在病床上无意中将六角幻方排列成功了。他惊喜万分，连忙找纸记录下来，了却了他多年的宿愿。几天后，他病愈出院。到家后却不幸地发现，他填的宝图不见了。

真是好事多磨，可是阿当斯没有灰心，他又继续奋斗了5年，终于在1962年12月的一天，有志者事竟成，阿当斯又重新填出了他盼望已久的宝图。

下面就是这个耗费了他52年心血的来之不易的六角幻方。

阿当斯随即将他的宝图拿给当时美国的幻方专家马丁·加德纳鉴定。面对这无与伦比的珍奇宝图，马丁博士欣喜万分，当即写信给才华横溢的数学游戏专家特里格。

特里格手捧宝图敬佩不已。这位专家也一头扎进了六角幻方，想在层数上作出突破。又耗费了不知多少心血，他才惊奇地发现，两层以上的六角幻方根本不存在。

1969年，滑铁卢大学二年级学生阿莱尔，对特里格的结论做出了严格的证明，并排除了一些不可能的情况，加上一些条件，利用电子计算机进行测试。仅用了17秒的时间，就得出了与阿当斯完全相同的结果。电子计算机向人类宣告：虽然普通幻方有千万种排法，但是，六角幻方却只有这一个，难怪阿当斯为之奋斗了52年。

当然阿莱尔用的方法是经过了分析，排除了绝大多数不可能的情况，所以在上个世纪六十年代计算机运算速度还不够快的情况下，只花17秒的时间就完成了求解。如果不想动脑筋，用暴力穷举法，这个解的尝试需要19的阶乘这么多次的尝试，这个数量是巨大的，也就是19*18*17*16*........*1这么多次尝试，就是普通的个人电脑来计算也需要很多年的时间吧。

我不想研究图形几何结构，于是想用最笨的穷举法进行尝试，毕竟这是计算机的强项。于是我设计了个方法，尝试的次数只需要19*18*17*16*15*14*13约等于两亿五千万次，在我电脑上大概运行了5个多小时。估计巨型计算机，只需要秒级的计算时间。我得到12个解，这12个解本质其实就是一个解。因为这一个解可以对称反转和旋转，得到12个位置本质一样的解。

这个六角幻方可以作为线性代数课程老师的教学案例，完全可以激发学生的挑战欲和学习兴趣，因为它的求解和矩阵的秩，初等变换，线性方程组的解的理论，线性空间等等有重大关系。只要解这么一道题，很多线性代数的内容就会自然搞懂了。我想如果线性代数老师是这么教学的，很多同学对抽象的线代至少也会多那么一些兴趣。

这里附带了一些六角幻方的问题。有兴趣的朋友可以尝试求解。明天我把我的解答贴出，也当做一个备份。

六角幻方的相关求解及代码如下，做个备份。程序采用穷举法，并不考虑空间结构的约束条件，进行了两亿五千多万次尝试（循环），实际耗时六个多小时。得到12个解，本质上是一种解的12种不同形式。同时下面还有其他各种问题都挺好的。

下图的每一列就是一个解。

解答：

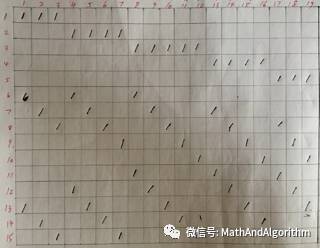
1. 需要19个未知数15个方程。

本题的解法就是，给每个小格子设置未知数，从x1~x19，建立方程。如下图所示

图1

图2

AX=0，即为齐次线性方程组。

下图就代表A矩阵，里面的数据填的地方都是1，不填的都为0.

图3

2. 计算前有4个空格可以填数。单从方程数量和未知数个数对比来看，未知数19个大于方程个数15个，若未经过求解，我们肯定会想，即使系数矩阵A的秩为15（最多也只是15），那么也多了4个未知数，这四个未知数作为自由参数，可以取任意值。从而对应六边形图中的某4个位置，可以任意填数。当然，这四个位置不固定，但也不是随便都可以（比如，六边形最外面的六条边，就不能随便填数，那样加起来不为0）

3. 计算后有7个位置可以任意填数。当把A矩阵输入MATLAB，计算其秩rank（A）=12，这说明A矩阵真正线性无关的就12行，一定可以化到最简，解是7个向量的线性组合。7个系数即为7个对应的未知数。（详细请查阅线性代数中齐次方程组内容）具体如下：

图4

如上图，利用MATLAB rref（A）函数对矩阵A进行 行化简，其实也就是相当于高斯迭代法求解AX=0 这一齐次线性方程组，图中可以验证rank（A）=12，从图中看出，选择x10，x11，x14，x15，x16，x18，x19.这七个变量作为可任填的自由系数。

即方程组改写为更容易的理解的形式如下，并把上述七个变量添加进去，得到19个解的通解形式：

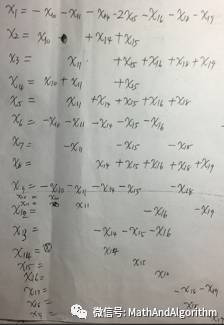
图5

解用向量的形式表示如下：

图6

上面的x10，x11，x14，x15，x16，x18，x19.这七个变量就是可以任意填的数，同时它们给出了位置信息。按照我前面给的x1~x19对应的位置信息，上面七个位置就是下面图中的圈出的红色六边形的位置，包含那七个变量。你可以先任意填那七个数，然后，其他位置的都可以在图中利用和为0直接都手算出来。另外也可以用上图的通解代入数据验算，两种方法结果一致！矩阵的不同化简方式会导致不同的自由变量选取，这会引起任意填的数的位置的改变，但是一定是像如图那样的位于角上的六边形位置。就好像把下面图不断旋转60，位置就改变不断改变，有六个这样的位置可以任意填数。

图7

4. 数字3和零空间的关系？首先说明下零空间，就是指满足AX=0这个齐次方程组的x的全体子空间。显然该零空间的维数为7（包含7个任意的的自由系数，所以维数为7）。那么3和7的关系就是3=7-4，4是第二问中未经计算的可任填的空格数。

即零空间维数（7）-（19-15）=3.

5. 显然是要考线性代数的理论，用的是暴力穷举法，所以最朴素的想法就是尝试19！这么多的次数。现在其实通过上述分析就知道，rank（A）=12，当现在每行每列的和为38时，我们一样将此时非齐次方程组AX=b的通解求出。 b为全是38的列向量，长度为15. 通过行化简（利用MATLAB rref函数计算），可得如下图8所示的通解形式。改变x10，x11，x14，x15，x16，x18，x19这些值，从1~19选取，互不相同，通过下面通解式子计算得到x1~x19，看看这十九个结果是否全部落在1~19，互不重复，是的话，满足要求，同时得到了一种填法！

需要尝试A(19,7)=19*18*17*16*15*14*13 这么多次，效率已经大大提高！

图8

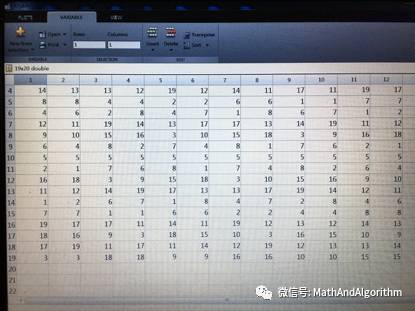
如下图9所示就是程序计算出来的一组解，把它旋转和对称，有12种情况。本质就是一种解而已。以上所有均在MATLAB程序中实现。

图9

现在解释MATLAB代码，MATLAB文件另附，文件中不含下面注释，下面红色部分为注释，特此说明：

以下是和为0的计算

a=zeros(15,19);

a(1,1:3)=1;

a(2,4:7)=1;

a(3,8:12)=1;

a(4,13:16)=1;

a(5,17:19)=1;

a(6,[1 48])=1;

a(7,[2 5 913])=1;

a(8,[3 6 1014 17])=1;

a(9,[7 11 1518])=1;

a(10,[12 1619])=1;

a(11,[8 1317])=1;

a(12,[4 9 1418])=1;

a(13,[1 5 1015 19])=1;

a(15,[2 6 1116])=1;

a(14,[3 712])=1; 以上实现A矩阵，大小15*19。注意MATLAB变量区分大小写，我这里先用小写a表示A矩阵

rank(a); 计算A矩阵的秩，运行完得到A的秩为12

A=rref(a); 对A矩阵进行行化简，得到如下：

图10

aEx=[aones(15,1)*38]; AX=b 非齐次方程组对应的增广矩阵

AEx=rref(aEx); 同上，对增广矩阵进行行变换，从运行结果可知，

rank(A) =rank(AEx)，所以非齐次方程组有解。AEx矩阵的内容就是A和下面的b，把b拼在A后面就得到AEx

B=[-1 -1 -1 -2 -1 -1 -1;

1 0 1 1 0 0 0;

0 1 0 1 1 1 1;

1 1 0 1 0 0 0;

0 1 1 1 1 1 0;

-1 -1 -1 -1 -1 0 0;

0 -1 0 -1 0 -1 0;

0 0 1 1 1 1 1;

-1 -1 -1 -1 0 -1 0;

1 0 0 0 0 0 0;

0 1 0 0 0 0 0;

0 0 0 0 -1 0-1;

0 0-1 -1 -1 0 0;

0 0 1 0 0 0 0;

0 0 0 1 0 0 0;

0 0 0 0 1 0 0;

0 0 0 0 0 -1-1;

0 0 0 0 0 1 0;

0 0 0 0 0 0 1; ];

B矩阵是手输入的，就是上图化简后的矩阵A的第10,11,14，15,16，18,19列移到右边变号得到的列向量所构成矩阵。其实B就是基础解系拼成的。

b = [76 0-38 0 -38 38 38 -38 38 0 0 38 38 0 0 0 38 0 0]';

b是从上面计算所得的AEx变量的最右边一列。因为我写代码是按顺序写的，前面先运行了，看AEx结果了，然后直接输入这里的。

x=[1 2 5 710 3 8]';

x=[3 3 7 4-10 -12 21]'; 这个x就是x10，x11，x14，x15，x16，x18，x19这七个任填的数据构成的列向量。这里给的两个x的验证数据就是我前面图7验证一验证二图中的数据。

XZero=B*x; 这里就是要验证“用任何软件MATLAB，SYMPY，JAVA实现填入实数使得每行或列都为0 填入的数字可以重复。” B*x 实现了图6的计算，结果保存在XZero变量中，一下子就得到了全部要填的数。。。可以更改x的值试试。

下面是和为38的计算。

temp=1:19;

template=round(temp');根据前面我的设计思路，就是要利用穷举法计算出满足非齐次线性方程组一种可能结果，如果是正确的结果的话，解一定是从1到19的整数，当然顺序是可以打乱的，所以到时候把计算的结果排序后同这里的template做对比，template的值是从1到19的升序的整数。

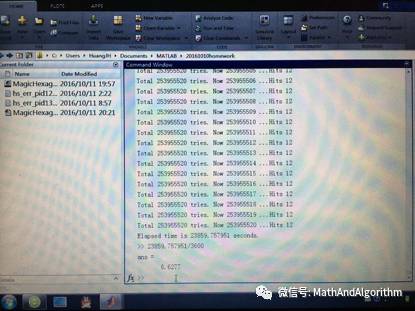
tic 开始计时，按照前面的解答，需要尝试A(19,7)=19*18*17*16*15*14*13 这么多次，约是两亿五千万次循环，所以这里蛮计时一下，大概需要5~10个小时。视电脑配置和程序运行方式不同而不同。

hits=0 检测一个结果，加1

Counts=0; 循环次数的统计累加

XTable=zeros(19,20); 符合要求的填数的结果变量。每个结果以列向量的形式存放，蛮假设有20个结果，弄个20列。。其实本质的解只有1个，总共有12种形式。道理很简单，你想象做好了一个解，你可以把整张直面翻过来，填数方式就变了，这叫做对称。也可以不断旋转60度，所以结合起来共12种解。

下面其实最关键的就是针对x10，x11，x14，x15，x16，x18，x19的所有取值情况（任意填的1~19的不重复整数）利用图8计算出结果，并加以判断合理的解。方法就是X=B*x+b; X 就是储存x1到x19的列向量，B，b是前述矩阵，x10，x11，x14，x15，x16，x18，x19按顺序构成列向量x。所谓的x10，x11，x14，x15，x16，x18，x19的所有取值，用到了nchoosek（）组合函数，和perms（）排列函数。再结合循环实现。关键是上述两个函数要弄清楚含义

CombinationX= nchoosek(1:19,7);构造1~19 里面任选七的所有组合，把结果以行向量的形式构成矩阵，注意是行向量!

[rowCountsCom,columnCountsCom]=size(CombinationX);取得组合结果矩阵的行数，rowCountsCom代表的是所有组合数，后面有个所有排列数，道理一样。

for i=1:rowCountsCom 遍历每一种组合，直到完成所有行数，即所有组合数，

PermutationX=perms(CombinationX(i,:));取当前第i个组合，计算其所有排列结果，同样结果以行向量形式存放在结果矩阵中

[rowCountsPerm,columnCountsPerm]=size(PermutationX);

for j=1:rowCountsPerm 同样遍历所有的排列情况

x=PermutationX(j,:);取其中的一种排列

X=B*x'+b; 计算全解x1~x19，注意这里使用x’，因为上面x是行向量，要转置为列向量。

XSorted=round(sort(X));算出来的结果要升序排序，同时round四舍五入避免因为计算过程导致的微小误差，引起程序误判结果不等

if (isequal(template,XSorted))结果相等的话

hits=hits+1 找中了一个，加一

XTable(:,hits)=X 最终结果添加到解的记录中，以列向量存放。

end

Counts=Counts+1;每一个内层循环加一计数。

fprintf('Total 253955520 tries. Now %d ...Hits %d\n',Counts,hits);这一行是为了避免MATLAB运行感觉太枯燥，让command window不断显示出统计的循环次数，相当于界面程序的进度条。。当然缺点就是会大大降低程序运行速度。因此不想要可以注释掉。

end

toc 计时结束。Tic开始，toc结束，很形象吧，按下表计时tic，按下toc结束计时。command window 会显示程序运行的总时间。按前面说的，本程序运行时间长，因为是穷举法，要进行两亿多次循环。下面是运行界面，还没运行完。到时候你可以自己去XTable里面查看结果。图9的结果就是运行出来的一组位置上的解，其他解就是位置变换而已。运行程序大概10分钟左右就会出来两组解，也就是此时显示Hits=2，这时候要是不想等所有的结果出来，可以按 ctrl+C终止MATLAB运行，然后查看XTable结果。