汪晓勤：它为数学文化融入数学教学开辟了一条途径

2018 年 7 月 11 日 科学出版社

“体现数学的文化价值”是2003版《普通高中数学课程标准》的课程理念之一。在新课程实施的十五年间，中学数学教育界有关数学文化的研究可谓如火如荼：数学文化校本课程不断涌现，数学文化专题会议屡见不鲜，数学文化融入数学教学的实践成了数学教育的热门课题。教育部考试中心在“2017年普通高考考试大纲修订内容”中提出增加数学文化内容，助推了数学文化热。在2017版《普通高中数学课程标准》将“认识数学的数学价值、应用价值、文化价值和审美价值”作为课程目标之一，将“重视数学实践和数学文化”作为“课程结构”的四个设计依据之一。我们有理由相信，数学文化全面融入数学课程的新时代已经来临。在这样一个新旧交替的特殊历史时期，中学数学教育界有必要总结过去十五年的数学文化研究和实践经验，为修订后的新课程实施提供借鉴。

数学文化融入数学教学

《文化视角下的数学教学研究》的作者、浙江省义乌中学王芳老师对于数学教育和数学文化有着深切的热爱。她长期潜心于数学文化与数学教学之间关系的研究，二十年如一日，不忘初心，兢兢业业，成就斐然。她不仅从教育学、心理学、现代课程论的角度研究数学文化，还采用了人类学、社会学的若干观点，这使她的研究达到了相当高的学术水平。《文化视角下的数学教学研究》从一线教师的现实需求出发，据理力证，得出数学文化融入数学学习的三种表现形态，实际上建立了判断一节数学课是否真正实施数学文化教育的标准，既有理论价值，又有实践指导意义。值得关注的是，《文化视角下的数学教学研究》采用了中学教师熟稔的数学思维、数学思想、数学概念的研究体式，将数学文化融入数学解题甚至数学计算的教学，为数学文化融入数学教学开辟了一条途径，是作者的一大创新。

数学史是数学文化的代言。将数学史融入课堂教学，是推进数学文化教育的有效策略之一。自2010年开始至今，王芳数学教育工作室开发了数十个数学史融入高中数学教学的课例（通常简称为HPM课例），这些课例大多已经发表，在国内产生了深远的影响。丽娃河畔，白彦山下，我和我的研究生与工作室的教师们常常相聚在一起，讨论有关主题的教学目标，解读有关主题的历史素材，研究历史素材的裁剪加工，一份份精彩的教学设计就在大家的思想碰撞之中产生。经历一次次的相聚和研讨，我们早已形成了一个学习共同体。王芳老师对于数学教学独到的见解，对数学史教育价值的深刻思考，让共同体的每一位成员都受益良多；而她的那份“课不惊人誓不休”的执着，深深地感染了每一位成员。在这个特殊的共同体中，我们收获了HPM的实践知识，一起快速成长。

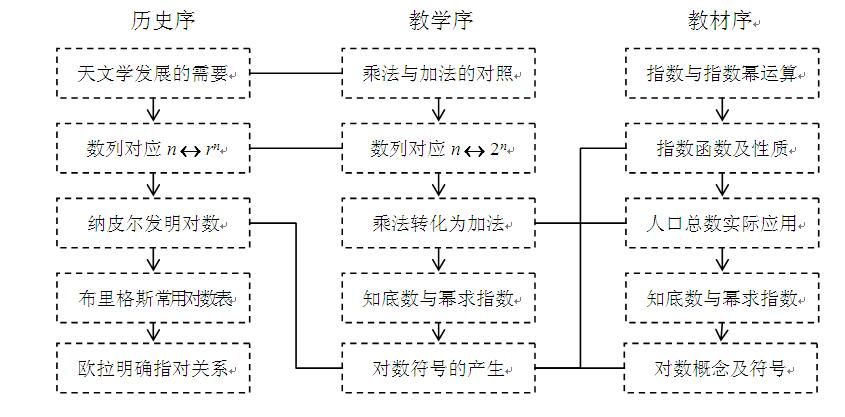
《文化视角下的数学教学研究》所选取的四个课例，既有再现当时上课场景的“教学实录”“课后调查反馈”，还有王芳老师在指导这些课例开发过程中的台前幕后、所思所行，这些难能可贵的第一手材料将是不少读者感兴趣的内容。作者从教材出发，始终关注学生的认知困难，然后从数学史中寻找教学的指南，把历史序、逻辑序整合为教学序，经过多次试教才最终形成这些课例。这些课例为更多HPM课例的开发提供了重要参考。同时，作者通过剖析这四个课例，有力地驳斥了那种数学史只是课堂教学的点缀、不过是看看图片听听故事的错误认识，阐明数学史在数学本质、数学探究、数学创造等方面所具有的深刻而独特的功能，使我们对HPM的未来充满信心和期待，也为中学教师不易驾驭的概念教学探寻了一种方向。另外，作者还调查访谈了这些HPM课例的执教者，总结出了三个阶段特征。当然，世上并没有终极完美的课例，每次试教付出代价的，不只是执教者，还有试教班级的学生。唯有最大限度地减少后来者的徒劳，才能更大力度地促进HPM教育的发展。

一位沉迷于数学文化二十年的教师，她的思想、她的行动、她的感悟、她的心路历程和她的丰硕成果，通过充满人文色彩的文字，展现在读者面前，诗意而动人。我深信，《文化视角下的数学教学研究》必将激活读者心中潜在的文化认知，吸引更多的数学教师抛开功利，去研究数学文化和数学教学之间的关系，营造充满文化芬芳的数学课堂，追求心中美好的数学教育理想。

本文摘编自王芳著《文化视角下的数学教学研究》一书序言部分，标题为编者所加。

《文化视角下的数学教学研究》

王芳著

ISBN 9787030580740

责任编辑：胡海霞

作者简介

王芳，教育硕士，浙江省义乌中学高级教师，义乌市高中数学王芳工作室负责人，首届中小学浙派名师培养对象、浙江省考试院高考命题专家库成员、华东师范大学数学教育研究生实践指导师、人教社课程标准实验教材中学数学培训团专家。

专注于数学文化教育，致力于HPM课例开发与青年教师专业发展研究。通过“内驱建构、思辨探求、人文渗透”，践行“智慧数学”的教育之道。参与教育部重点基金项目及多个省级课题，多次参编浙江省教育厅基础教育教学指导用书。在《课程·教材·教法》《数学教育学报》《中学数学教学参考》等刊物上发表学术论文四十余篇。

内容简介

本书紧扣中学数学教学实际，既从中观层面探讨数学文化与教育过程的衔接问题，又从微观层面研究数学文化进入高中课堂的具体实施，为中学数学教育界同仁开展数学文化教育提供参考或借鉴。本书共7章，内容包括数学文化之不容或缺、数学文化与数学学习的融合、数学文化的课堂诠释、数学思维的人文意蕴、数学思想的智慧启迪、数学概念的HPM重构、数学史料的理性体验。本书通过研究数学文化之于学习过程的表现形态，突破数学文化的“隐性”局限；使数学文化与双基教学相结合，谋求两者的双赢；提高高中数学的文化品位，改进青年学生的数学观与学习观。

第1章数学文化之不容或缺
1.1对于数学教育传统的反思
1.1.1数学双基教学需要文化的润泽
1.1.2数学交流需要开放的文化氛围
1.1.3数学知识需要丰富的文化素材
1.2来自新课程的教育新诉求
1.2.1显化数学课程体系的文化特质
1.2.2拓宽数学文化进入课堂的途径
1.2.3树立正确的数学文化教育理念
1.3实施数学文化教育的现实基础
1.3.1已有的理论成果
1.3.2多元的实践支持
1.3.3研究评述
第2章数学文化与数学学习的融合
2.1高中学生的文化认知特点
2.1.1同喻性
2.1.2不均衡性
2.2数学文化在高中数学学习中的表现形态
2.2.1群体的活动性
2.2.2系统的开放性
2.2.3知识的默会性
2.3开展实践的“可视”框架
第3章数学文化的课堂诠释
3.1数学文本的文化解读
3.1.1以应用为链，延伸数学触角
3.1.2以语言为渠，品尝文化韵味
3.1.3以人为鉴，体验解题韵律
3.1.4以史为辅，挖掘文化底蕴
3.2文化意义上的“做”数学
3.2.1在协商中建构数学知识

3.2.2在合作中渗透数学思想
3.2.3在交流中体现人文关怀

3.3文化向度的数学教学观

第4章数学思维的人文意蕴
4.1数据与结构的隐喻
4.1.1亲密的“不等家族”
4.1.2蕴含在数据和结构中的摩斯密码
4.1.3解题中的运用
4.2角与名的较量
4.2.1三角公式中的“刀光剑影”
4.2.2角与名，谁先行
4.2.3解题中的运用
4.3穿越向量丛林
4.3.1向量：精钢可化绕指柔
4.3.2“向量丛林”的弯道超越
4.3.3解题中的运用
4.4数列的通妙法门
4.4.1数列“孪生子”
4.4.2用通法还是妙解
4.4.3解题中的运用
4.5游走在垂线与垂面之间
4.5.1重中之重是垂线
4.5.2发生在垂线与垂面之间的视觉游戏
4.5.3解题中的运用
4.6得韦达定理者得天下
4.6.1率土之滨，莫非“韦达”
4.6.2探秘“王者之道”
4.6.3走出“量”的迷阵
4.6.4解题中的运用
第5章数学思想的智慧启迪
5.1图象“编织”的艺术