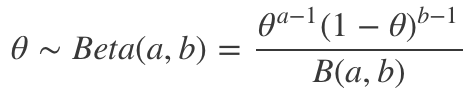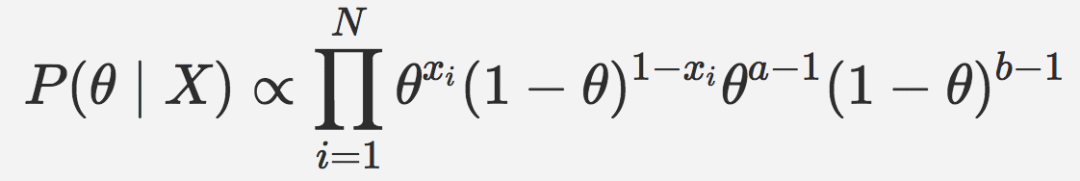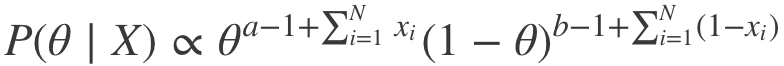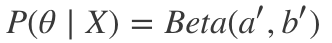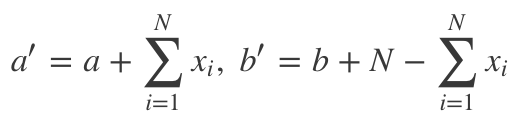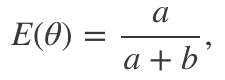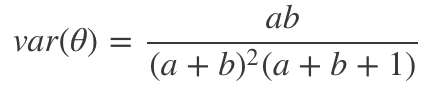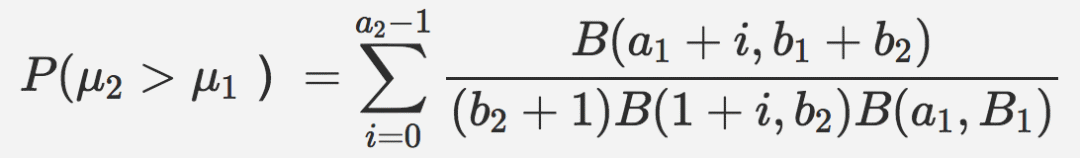基于汤普森采样的贝叶斯A/B测试

会员服务 ·

基于汤普森采样的贝叶斯A/B测试

2018 年 8 月 12 日 论智

来源：zlatankr.github

编译：weakish

编者按：和Google产品分析Zlatan Kremonic一起探索A/B测试的贝叶斯方法背后的理论。

本文将探索A/B测试的贝叶斯方法背后的理论。这一方法最近得到了广泛认同，并在一些情形下取代了流行的频率方法。在讲述理论之后，我们将查看一个实例。

频率统计

频率统计以收集数据、测试假设这一传统方法为中心。频率统计分为以下步骤：

形式化假设。
收集数据。
计算基本的测试统计，包括p值和置信区间。
决定是否驳回零假设（null hypothesis）。

频率统计的重要假定是参数是确定的，不过我们并不知晓。我们接下来收集的数据是那些参数及其分布的一个函数。用数学可以表达为：

其中X是数据样本，θ是零假设下的数据分布，戴帽θ是观测到的参数。

总结科研报告的数据时，这一方法非常有用。置信区间的应用为我们提供了非常直观地理解观测到的参数的方式。不过，这一频率方法有一些缺陷：

当我们发现p值明显增加时，较早停止测试会增加得到假阳性结果的几率。
我们无法测量研究结论为真的概率。
p值容易被误解。
试验必须全部事先指定，这可能导致看起来自相矛盾的结果。

多臂老虎机问题

在我们跳到贝叶斯推理之前，先在一个有用（且经典）的场景下考察我们的问题，这很重要。在多臂老虎机问题中，我们在一家赌场玩老虎机。给定不是所有的老虎机返水率相同这一条件，如果我们同时玩两台老虎机，我们将开始发现两台老虎机的结果不同。这导致了“探索v.s.利用困境”，迫使我们决定到底是利用高返水的机器，还是探索（随机）选项以收集更多数据。不管我们选择利用的程度如何，我们都在让我们的行为适应观测数据，这正是强化学习的一般假定之一。我们的目标是通过提高我们正做出正确决策的确定性，最大化返水，最小化损失。

处理多臂老虎机问题有很多策略，包括Epsilon-Greedy算法和UCB1算法，不过，也该让贝叶斯推理出场了。

贝叶斯统计

贝叶斯统计以贝叶斯定理为中心：

在我们试图得出关于给定数据集的参数的结论的科研问题中，我们可以将参数视作随机变量（有自己的分布）：

这里，

P(θ|X)称为后验，意为给定数据X，关于参数θ的新信念。
P(X|θ)称为似然，回答给定当前参数θ有多大可能观测到我们的数据。
P(θ)是先验，意为我们关于θ的旧信念。
P(X)是P(X|θ)P(θ)dθ的积分，但因为它并不包含θ，可以直接忽略这一点，将它作为一个归一化常量。

现在我们看到了贝叶斯范式转变。和频率方法不同，这里我们收集数据的前后都考虑到了参数的分布。知晓参数的分布让我们可以给参数估计分配给定的置信度。

但我们如何知晓后验分布呢？答案在“共轭先验”这一概念之中：如果先验概率分布和后验概率分布同属一个家族，那么它们称为共轭分布，且先验称为似然函数的共轭先验。简单来说，如果我们知道似然函数的分布，我们就可以确定后验和先验的分布。

让我们来看一个例子，假设我们正测量点击率（某人是否点击一则广告）。因为我们测量的是二值输出（点击、没点击），所以我们处理的是伯努利分布，这意味着似然为：

伯努利分布的共轭先验是贝塔分布：

其中B(a, b)为贝塔函数。

我们需要求解后验，首先结合似然和后验：

上式可以简化为：

因此，我们可以看到，事实上P(θ|X)确实属于贝塔分布，只不过超参数略有变动。由此我们得到：

其中，

在我们的点击率问题中，a' = a + 点击数，b' = b + 未点击数。

直觉上，这很合理。因为它告诉我们，后验分布是收集数据的函数，且后验分布可以用作更多样本的先验，其中的超参数直接加上新得到的额外信息。

进一步查看下贝塔分布，我们注意到这一分布的均值为：

这和最大化似然时得到的值相同。最后，当a和b增加时，贝塔分布的方差递减，可类比频率方法中置信区间的表现：

例子：汤普森采样

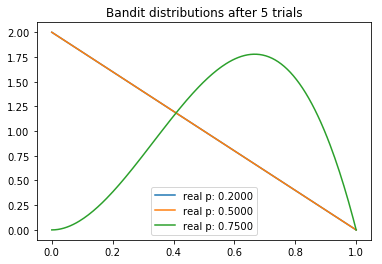
在这个例子中，我们将演示如何使用汤普森采样基于贝叶斯推理解决多臂老虎机问题。我们将使用2000次测试，而三臂的返水率为0.2、0.5、0.75. 首先，我们定义具有给定概率的Bandit（老虎机）类。该类提供一个pull（拉）方法，基于其概率返回奖励或损失（1或0）。我们也能更新a、b，并使用这些值从所得贝塔分布中取样。

  
  
    
   
   
     import matplotlib.pyplot as plt
   
   
     import numpy as np
   
   
     from scipy.stats import beta
   
   
     
   
   
     
   
   
     NUM_TRIALS = 2000
   
   
     BANDIT_PROBABILITIES = [0.2, 0.5, 0.75]
   
   
     
   
   
     class Bandit(object):
   
   
       def __init__(self, p):
   
   
         self.p = p
   
   
         self.a = 1
   
   
         self.b = 1
   
   
     
   
   
       def pull(self):
   
   
         return 1 if np.random.random() < self.p else 0
   
   
     
   
   
       def sample(self):
   
   
         return np.random.beta(self.a, self.b)
   
   
     
   
   
       def update(self, x):
   
   
         self.a += x
   
   
         self.b += 1 - x

下面，我们将定义一个函数绘制老虎机的贝塔分布：

  
  
    
   
   
     def plot(bandits, trial):
   
   
       x = np.linspace(0, 1, 200)
   
   
       for b in bandits:
   
   
         y = beta.pdf(x, b.a, b.b)
   
   
         plt.plot(x, y, label="real p: %.4f" % b.p)
   
   
       plt.title("Bandit distributions after %s trials" % trial)
   
   
       plt.legend()
   
   
       plt.show()

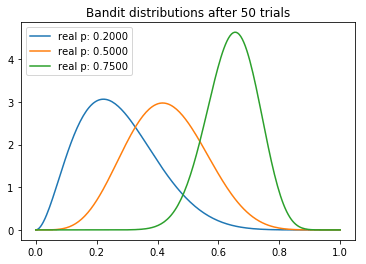
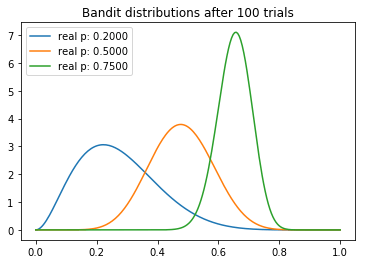
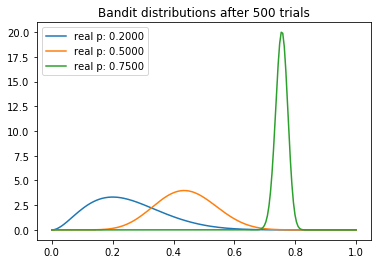
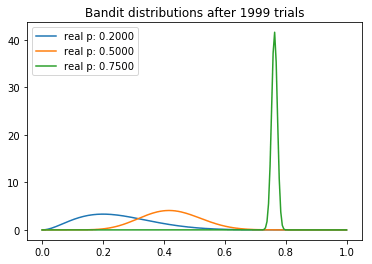
现在，开始我们的试验。首先，我们初始化三台老虎机。我们将根据预先确定的sample_points绘制它们的分布。每次测试时，我们从每台老虎机的分布中取样，并选择返水率最高的老虎机。被选中的老虎机将有机会拉动它的拉杆，进而更新其a、b值。

  
  
    
   
   
     def experiment():
   
   
       bandits = [Bandit(p) for p in BANDIT_PROBABILITIES]
   
   
     
   
   
       sample_points = [5,50,100,500,1999]
   
   
       for i in xrange(NUM_TRIALS):
   
   
     
   
   
         # 从每个老虎机取样
   
   
         bestb = None
   
   
         maxsample = -1
   
   
         allsamples = [] # 收集这些数据以便调试时打印
   
   
         for b in bandits:
   
   
           sample = b.sample()
   
   
           allsamples.append("%.4f" % sample)
   
   
           if sample > maxsample:
   
   
             maxsample = sample
   
   
             bestb = b
   
   
         if i in sample_points:
   
   
           print "current samples: %s" % allsamples
   
   
           plot(bandits, i)
   
   
     
   
   
         # 拉动样本最大的老虎机的拉杆
   
   
         x = bestb.pull()
   
   
     
   
   
         # 更新刚刚拉动拉杆的老虎机的分布
   
   
         bestb.update(x)