修订 | 听说蜜蜂不仅会数学，还挺厉害？

作者：

Scarlett Howard  皇家墨尔本理工大学博士候选人

Adrian Dyer  皇家墨尔本理工大学副教授

Jair Garcia 皇家墨尔本理工大学研究员

翻译：獭哥

校对：尹涛

最近发表在《Science Advances》杂志上的一项新研究显示：小小的蜜蜂竟然可以使用符号来进行基本的数学运算，包括加法和减法。

蜜蜂的大脑十分微小 - 但他们可以学习基本的算术

尽管蜜蜂只拥有不到一百万个神经元的大脑，最近的研究却表明蜜蜂可以解决复杂的问题——比如理解零概念。

蜜蜂一直是探索神经科学问题的高价值模型。在我们的最新研究中，我们决定测试他们是否可以学习进行简单的算术运算，比如加法和减法。

加法和减法运算

当我们还是孩子的时候，我们就知道加号（+）表示我们必须添加更多的数量，而减号（- ）表示我们必须减去一些数量。

为了解决这些问题，我们必须要有长期和短期记忆。在进行运算时我们使用工作（短期）记忆（work memory）来管理数值，在记忆那些加减法则的时候我们会用到长期记忆（long-term memory）。

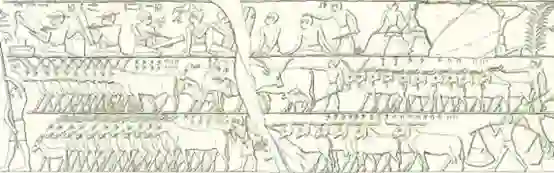
尽管加法和减法等运算的能力并不简单，但它在人类社会中至关重要。有证据显示，在公元前2000年埃及人和巴比伦人已经在使用算术了，比如说，当他们卖掉了一些家畜的时候，他们会用算术来统计家畜的新数量。

这个场景描绘了家畜的数量（由埃及学家Lepsius复制）。 

图片来源：Wikimedia commons, CC BY

但算术思维的发展是否需要一个像灵长类大脑那样大尺寸的大脑呢，其他动物是否也面临类似的问题，从而使他们也能够进行算术运算呢？于是我们用蜜蜂做实验，探索了这个问题。

如何训练蜜蜂

蜜蜂是中心觅食者 - 这意味着如果某个地方能够提供良好的食物来源，觅食中的蜜蜂就会返回这个地方。

我们在实验期间为蜜蜂提供高浓度的糖水，因此个体蜜蜂（所有雌性）就持续不断地回到实验中为蜂巢收集营养。

在我们的设置中，当蜜蜂选择了正确的的数字（见下文）时，她会获得糖水奖励。如果她做出了错误的选择，她就会收到一种苦味的奎宁水。

我们使用这种方法在四到七个小时内教蜜蜂学习加法或减法。每次蜜蜂吸满了糖水，她就回到蜂巢，然后再继续回到实验的地方学习。

蜜蜂的加法和减法

我们让蜜蜂在一个Y形的迷宫形装置里进行单独训练。

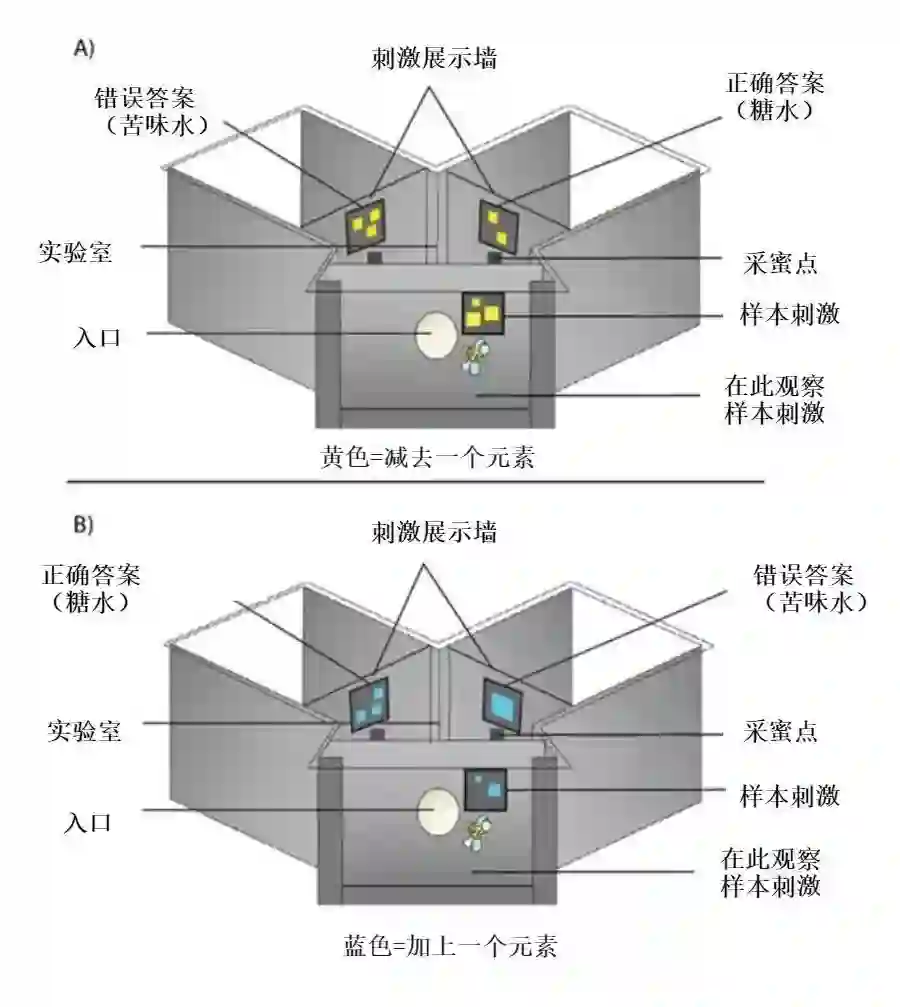
蜜蜂飞到Y型迷宫的入口处，先观察迷宫门口由一到五个形状组成的一系列元素，这些形状可能是方形或者其他形状。这些元素有两种颜色，要么是蓝色的，要么是黄色的，蓝色意味着蜜蜂必须进行加法运算（+1）。如果是黄色，蜜蜂就要进行减法运算（-1）。

不管任务是加法还是减法，迷宫都是一侧设置为正确答案，另一侧设置为不正确答案。在整个实验过程中，正确答案位于哪一侧会随机决定，因此蜜蜂不会只学会飞向Y型迷宫的某一侧。

在观察完初始数字之后，每只蜜蜂将通过一个洞进入迷宫，在那里她可以根据自己受到的训练来选择飞到Y型迷宫的左侧或右侧。

用于训练蜜蜂的Y迷宫装置，（A）减法和（B）加法  Scarlett Howard

在实验开始时，蜜蜂会做出随机选择，直到他们能够找到解决问题的方法。最终，在超过100次学习之后，蜜蜂终于明白蓝色意味着+1，而黄色意味着-1。然后，蜜蜂就可以将规则应用于新数字。

在使用新数字进行测试的时候，对于一种元素的加减法，受过训练的蜜蜂在64-72％的时间里都是对的。如果蜜蜂是被随机选择的，那么他们在测试中的表现就会与我们的预期明显不同，我们称之为机会水平表现（50％正确/不正确）。

因此，我们在 “蜜蜂学校”的Y迷宫中的是允许蜜蜂学习如何使用算术运算符来进行加或减。

为什么这对蜜蜂来说是一个复杂的问题？

加减法这种数字运算对于蜜蜂来说之所以是复杂的问题，是因为这种运算需要二级处理。第一级要求蜜蜂理解数值属性的价值。第二级要求蜜蜂用工作记忆对数字属性进行心算。

除了这两个过程之外，蜜蜂还必须在工作记忆中进行算术运算——加上或者减去的数字“一”的行为，在视觉上是不存在的。当然，加一或减“一”的想法是蜜蜂在训练过程中必须解决的抽象概念。

蜜蜂不仅会做数学题，他们的窝从外观上看也明显具有数学特征，一排排完美的六边形组成了一个整齐的二维阵列。蜂窝里的六边形就是一个个小房间，每个房间可以容纳一个蜂蛹，也可以储存蜂蜜。它的内部是一个个几乎相同的六边形腔室，结构非常优美。

普通蜜蜂一般沿垂直方向建造蜂窝，六边形巢穴是水平朝向的，而黄蜂则沿着水平方向建造蜂窝，六边形巢穴是垂直朝向的。

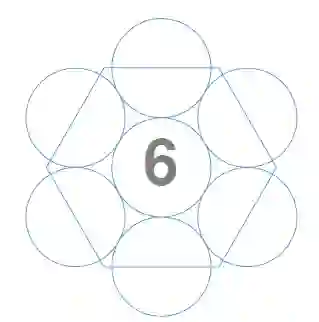
乍一看，就像一项惊人的工程。但这里有一个诀窍，即“密堆积”。如果把大量形状相同的圆形物体（例如硬币）放到桌子上，然后摇晃桌子，让这些物体尽量挤成一团，你就会发现这些物体排成了蜂窝状结构。实际上，这些蜂窝状结构不是绝对规整的，蜜蜂的蜂窝同样不太规整。大约100年前，数学家证明了蜂窝体现了图形形成的一个重要特征：同一个基本单元被反复应用，6个圆正好可以包围一个同样大小的圆。蜂窝是将近似圆形的图形紧密结合在一起的一种有效方法，大自然在很多时候都要借用这个方法，因此六边形和与之相关的蜂窝在物理学和生物学的图形形成中都扮演着重要角色。

现在，蜜蜂在数学领域也大显身手，蜜蜂可以将简单的算术和符号学习进行结合的研究已经被许多研究领域确定并扩展出更多的研究，比如其他动物是否可以做加减法呢。

对于人工智能和神经生物学的意义

人工智能以及计算机能够在多大程度上实现自我学习的问题一直备受关注，我们的新发现表明，像蜜蜂一样的微型大脑也可以通过学习符号运算来做加减法，这暗意味着，可能会有新的方法将长期规则和工作记忆的交互作用结合到设计中，以改善人工智能快速学习新问题的能力。

原始文章请点击“阅读原文”。

本文部分摘编自《迷人的图形》

相关书籍推荐

自然界中存在许多迷人的图形，小至一个分子，大至整个宇宙，你都可以发现无处不在的数学结构和神 奇的数学之美。

斑马的条纹是如何形成的？

天体的运行轨道为什么呈椭圆形？

蜂窝的结构为什么是六边形？

雪花的形状是如何产生的？

本书从一个简单常见的问题入手——雪花的形状是如何产生的，探讨这种既规则又不规则的图形为何会存在。石榴、海星、花瓣中也隐藏着形形色 色的图形，在这些图形背后，是主宰着自然甚至整个宇宙的数学法则。