什么是维度？

2018 年 3 月 13 日 中国物理学会期刊网 原理

经授权转载自“原理”微信公众号

在过去的一个世纪中，对空间的几何描述成为了理论物理学追求的主要课题。我们普遍接受的空间是三维的，广义相对论描绘了一个四维的宇宙，而弦论则说宇宙有10维，它的扩展版本M理论认为宇宙有11维，最近甚至还出现了新的24维版本。四维以上的世界究竟是什么样子？它们又有什么样的意义呢？

作者：Margaret Wertheim

翻译：顾金涛刘博尧

审校：张克文王妍琳

本文经授权转发自「环球科学」（ID：huanqiukexue）

伏案写作，抬手打开台灯，落手拉开抽屉拿出笔，伸手让指尖划过一尊奇形怪状的小雕像——那是我妹妹送我的幸运符——背过手拍了拍蜷缩在我身后的猫。右手边是为文章准备的研究笔记，左手边则是一堆“必做”的事项（账单和信件）。上下、前后和左右，我以这个世界的直角坐标轴为刻度，在自己的三维宇宙中航行。

我们的建筑、我们的教育和我们的字典告诉我们：空间有三个维度。牛津字典定义空间（space）为“一片连续的自由的，可获得的或者可被占用的区域……所有东西都在高度、深度和宽度这些维度中存在和移动。”18世纪时，康德（Immanuel Kant）称三维的欧几里得空间是一种先验必然。如今，随着计算机生成的图像和电子游戏的渗透，我们始终处于一个似乎是公理的笛卡尔坐标系表征中。站在21世纪的视角，这一点近乎不证自明。

不过，“我们生活的空间具有数学结构”这个观念，是西方文化的激进创新，它迫使我们抛弃长久以来对现实本质的信念。尽管现代科学的诞生通常被谈论成对自然界的机制机械性解释的过渡，但我们可以看到，更加重要，当然也更加持久的是另一种转变：我们对空间的概念变成了一种几何建构。

在过去的一个世纪中，对空间的几何描述成为了理论物理学追求的主要课题，从阿尔伯特·爱因斯坦（Albert Einstein）开始，学者们都试图将自然界所有基本作用力解释成空间形状本身的副产品。尽管在局部层次我们被训练成将空间想成三维，广义相对论描绘了一个四维的宇宙，而弦论则说宇宙有10维，它的扩展版本M理论甚至认为宇宙有11维。有些宇宙模型将宇宙描绘为26维，最近还出现了让纯数学家们兴奋不已的24维版本。但这些“维度”到底是什么？谈论一个10维的空间存在又有什么样的意义呢？

什么是“空间”？

要理解现代数学中对空间的描述，需要把空间想成物质可以占据的舞台。至少，“空间”应该是某种延展出去的东西。这对我们来说似乎是显而易见的，但亚里士多德却十分厌恶这个观点，他对物理世界的概念定义，在古典时代晚期和中世纪统治了西方思想界。

严格地说，亚里士多德的物理学中并不包括空间理论，只有位置的概念。想象桌子上的一个杯子，对亚里士多德来说 ,杯子被本身也是实体的空气环绕，在他的世界图景中，并不存在真正“空无一物”的空间，这里只有空气和杯子者两种物质的边界。对于亚里士多德来说，“空间”（如果你愿意这么称呼的话）只是杯子和环绕在其旁边的无限小边界。如果空间不能扩展，那么任何东西都不会在空间之中。

亚里士多德之前几世纪，留基伯（Leucippus）和德谟克利特（Democritus）就已经提出了一种调用内含空间的“原子化”视角来描述现实世界的理论，他们认为，在虚空中移动的微小粒子(或原子)组成了物质世界。但亚里士多德拒绝原子论,声称虚空的概念在逻辑上不自洽，他说根据定义，“什么都没有”是不可能存在的。摆脱亚里士多德对虚空的异议，从而形成延展空间的概念，是一个世纪课题。直到伽利略和笛卡尔在17世纪早期，将延展时空变成了现代物理的基石之一，这才让这个创新的设想发展成熟。就像1924年美国哲学家埃德温·伯特（Edwin Burtt）评论的那样，对这两个思想家而言，“物理空间与几何领域等同起来”，这里的几何领域，也就是如今学校教的三维欧几里得几何。

早在物理学家接受欧几里得视角之前，画家已经在空间的几何概念上先行一步。多亏了他们，我们才在概念框架中跨出一大步。在中世纪晚期，在新兴起的柏拉图和毕达哥拉斯的思潮的影响下（这两位也是亚里士多德的学界对手），“上帝按照欧式几何定律创造世界”的观念开始渗透进欧洲。因此，当艺术家想要正确地描绘世界，他们应当模仿造物主的表现手法。从14世纪到16世纪，诸如乔托（Giotto）、保罗·乌切洛（Paolo Uccello）和皮耶罗·德拉·弗朗西斯卡（Pierodella Francesca）等艺术家建立了现在所知的“透视”技巧，这种风格在当时被称为“几何图像”。通过有意识地探索几何原理，这些画家逐渐学会如何构建三维空间内物体的图像。在这个过程中，他们重新编译了欧洲人的思维，使他们用欧几里得的方式来看待空间。

历史学家塞缪尔·埃杰顿（Samuel Edgerton）在《乔托几何的遗产》（The Heritage of Giotto’sGeometry，1991）中叙述了这段值得铭记的延续，他注意到我们对亚里士多德空间观的摒弃，有一部分是来自透视画缓慢长期的影响：当人们站在透视画前，发自内心地感受，就好像他们透过墙壁看到了另一边的一个三维世界。而其中的非凡之处在于，当哲学家和科学家小心翼翼地挑战亚里士多德的空间概念时，艺术家们却通过对感知的依附，在知识界的疆域中大出风头。用大白话说，透视的表现方式是一种虚拟现实，就像如今的VR游戏一样，试图给观者制造一种幻觉——他们被转移到了另一个在几何上一致，心理上可信的世界。

透视表达的欧几里得幻想空间逐渐印刻在了欧洲人的意识中，并被笛卡尔和伽利略接受为现实世界的空间。值得补充的是，伽利略自己就受过透视法的训练。他对深度的表现能力是他在对月亮的开创性绘画中的一个关键特征，他画出了月亮上的高山和峡谷，暗示了月亮和地球一样是固态的实体。

通过接受透视画作的空间观，伽利略可以用数学法则展示诸如炮弹等物体的运动方式。空间本身就是一种抽象——一种没有特征、不活跃、不可触摸、不可感知的虚空，它唯一的可知性质就是它的欧几里得形式。到了17世纪末期，牛顿（Isaac Newton）将伽利略的视角拓展到整个宇宙，延展出潜在的无限的三维真空——向所有方向永恒延伸的广阔无物的“空”。“实在”的结构就这样从哲学和理论问题转换到了几何命题上。

维度，数学的图像化

当画家用数学工具开发出创作的新方法时，科学革命也曙光初现，笛卡尔探索了将数学关系进行图像化的方法。在这个过程中，他形式化了“维度”的概念，不仅在我们的意识中注入了一种看待世界的新方式，更创造了一种新的科学工具。

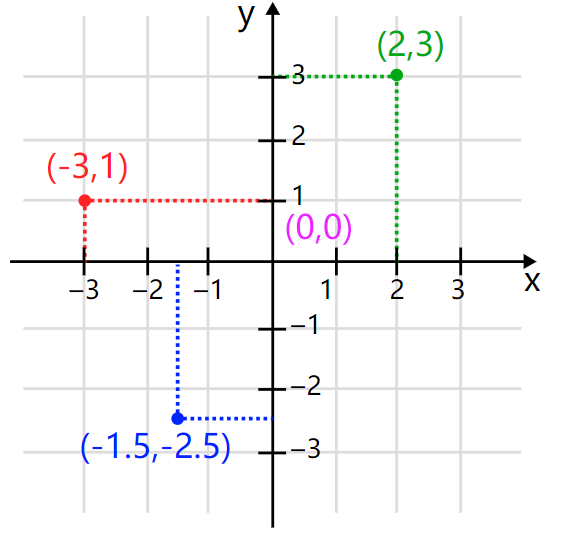
当今几乎所有人都能认出笛卡尔的天才成果，笛卡尔坐标系，一个带有x轴和y轴的直角坐标系统。

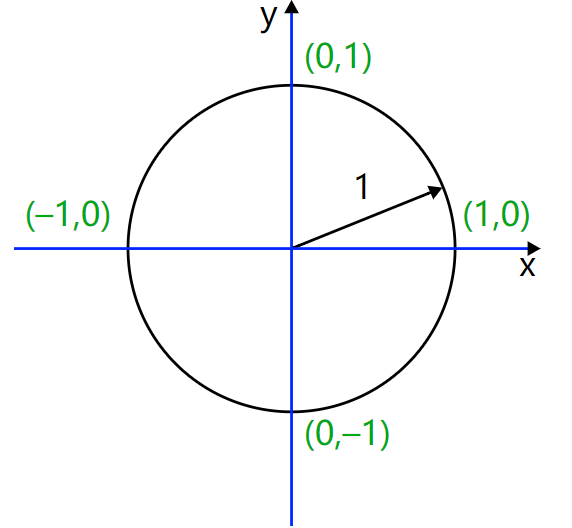
根据定义，笛卡尔平面是一个二维空间，因为我们需要两个坐标来定义其中的任意一个点。笛卡尔发现在这个框架下他可以将几何形状与方程联系在一起：一个半径为1的圆就可以用等式x²+ y²= 1来描述。

我们在平面上画的一系列图像都可以用方程来描述，这种“解析几何”或者“笛卡尔几何”，很快就成为牛顿和莱布尼兹发明的微积分的基础，之后的物理学家以此来描述运动。理解微积分的一种方式是研究曲线，它让我们可以规范地定义曲线在哪里最陡，或者它在哪里达到局部极小或者极大。在对运动的研究中时，微积分使我们能够分析和预测被抛出的物体在哪里可以达到最高点，或者何时沿着弯曲轨道滑落到特定的速度。微积分发明以后，它已经成为了科学几乎所有分支的重要工具。

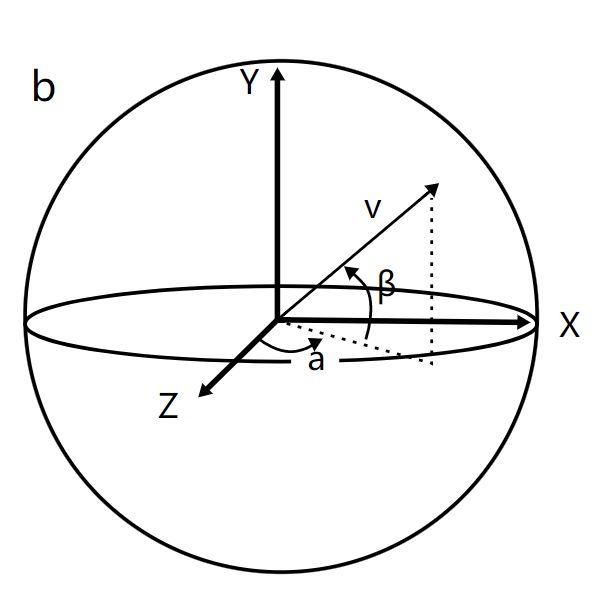
从上一张图的基础上，我们可以很容易想到如何再加一条坐标轴。通过x,y,z轴我们就可以描述一个球面，一个半径为1的球面的方程是：x²+ y²+ z² = 1。

通过三根轴，我们可以描述三维空间的形式。同样地，每个点都可以被三个坐标唯一确定，这是使空间成为三维的必要条件。

我们再接再厉，再加到第四个维度会怎样？姑且把多出来的这个参数称其为“p”，现在我可以写下一个方程，来描述这个存在于四维空间的球面：x²+ y²+ z²+ p²=1。我不能把这个物体画给你看，但是从数学上看，再加另一个维度是一个合理的操作。这个“合理”指的是不存在逻辑上的矛盾，即没有理由不能这么做。

我可以继续这样做，增加更多维度。我可以定义一个五维空间中的球面，其空间拥有5个坐标轴（x,y, z, p, q），球面方程x²+ y²+ z²+ p²+ q²= 1。再定义一个六维的：x²+ y²+ z²+ p²+ q²+r² = 1，等等等等。

尽管我可能难以将这些高维球面可视化，我却可以用符号来描述它们，理解数学历史的方式，就是抱着开放性的心态，超越那些看似合理的事情。这就是查尔斯·道奇森（CharlesDodgson）在《爱丽丝镜中奇遇记》（Through the Looking Glass, and What Alice Found There，1871）中描述的“早餐前做6件不可能的事”。

数学上，我可以描述一个任何维数的球面。我只要不断添加新坐标轴就可以了，数学家称之为“自由度”。按照习惯它们被命名为x₁、x₂、x₃、x₄、x₅、x₆等等。就像笛卡尔平面上的任意一点可以被两个（x,y）坐标描述一样，任何一个在17维空间中的点都可以用一组17个的坐标（x₁,x₂,x₃,x₄,x₅,x₆… x₁₅,x₁₆,x₁₇）描述。这样高维空间中的球面被称为流形（manifolds）。

从数学视角，一个“维度”只不过是另一条坐标轴（自由度），最终成为一个纯粹的符号概念，并不一定与物质世界的任何东西发生联系。在1860年代，曾影响过路易斯·卡罗的先锋逻辑学家奥古斯都·德·摩根（Augustus De Morgan）总结了这个领域越来越抽象的观念，强调数学是纯粹的“符号的科学”，并不需要与自身之外的任何东西关联。数学在某种程度上，是在想象的空间中驰骋的逻辑。

数学家在理念世界中自由玩耍，物理学家则不同，他们被限制在自然界中，至少在原则上，必须与物质世界保持一致。然而这一切还是宣告了一种解放的可能性，因为既然数学允许多于三个维度，而且我们认为数学在描述世界中很实用，我们怎么知道物理空间的维数被限制为3个？尽管伽利略、牛顿和康德将长度、宽度、高度视为公理，我们的世界就不会有更多维度了吗？

从三维出发

宇宙有多于三个维度这个观念，又一次通过艺术形式进入公众意识，这一次是来自文学的猜测，其中最著名的是数学家埃德温·A·艾伯特（Edwin A Abbott）的《平面国》（Flatland，1884）。这部迷人的社会讽刺作品讲述了住在平面国上的一位谦卑的方块先生的故事。有一天，一个三维生物，球大人，前来拜访并带方块先生去了立体王国。在这个有体积的仙境，方块先生看见了一个三维版本的自己——立方体，之后开始幻想推进到第四个、第五个和第六个维度。他很疑惑，为什么没有超立方体和超超立方体？

悲哀的是，当方块先生回到平面国，他被视为疯子，关到了疯人院。这个故事另一个值得称道之处在于，它意识到了鼓吹社会惯例的危害。当方块先生声称有其它维度的空间时，他同时也力图证明其他维度生物的存在——他是一个数学怪人。

在19世纪晚期和20世纪早期，包括许多许多数学家、作家查尔斯·汉顿（Charles Hinton，发明了四维立方体的名称“tesseract”的和科幻作家）、艺术家达利（Salvador Dalí）和神秘主义思想家邬斯宾斯基（P D Ouspensky）探索了第四维度的想法以及人们碰到它们会意味着什么。

之后，在1905年，当时名不见经传的物理学家阿尔伯特·爱因斯坦发表了一篇论文，将真实世界描绘为一个四维的宇宙。在他的“狭义相对论”中，时间是空间的三个经典维度之外的另一维度。在相对论的数学表述中，四个维度都是紧密相连的，也形成了时空这一词汇。这种对时空的组合绝对不是任意的。通过这种途径，爱因斯坦发现有一种非常强大的数学方法出现了，这种方法超越了牛顿力学，并且可以对带电粒子的行为做出预测。只有在四维的模型中才可以使电磁学得到完整精确的描述。

相对论绝不是简单的文字游戏，尤其是在爱因斯坦将狭义相对论扩展为广义相对论后。多维宇宙有了更深层的物理含义。

在牛顿的物理图像中，物质在自然力尤其是引力的影响下随着时间在空间中移动。空间，时间，物质和力是现实中相互独立的几个物理要素。在狭义相对论中，爱因斯坦强调时间和空间是统一的，这就将基本的物理要素由四个减少到三个：时空，物质和力。广义相对论又进了一步，将引力描述为时空本身的结构。从四维时空的角度来看，引力只不过是空间形状产生的效果罢了。

为了理解这一意义重大的物理图像，我们先想象一下它的二维类比。假如有一张有弹性的薄膜，我们在上面画上直角坐标系的网格。现在我们在网格上放置一个保龄球。在保龄球周围，薄膜就会有伸展形变，所以一些点之间的距离就会变得更远。我们通过使这个空间不均匀，改变了空间中测量得到的固有距离。广义相对论说这种空间形变是诸如像太阳一样的大质量物体对时空造成的影响。这种时空本身和直角坐标之间的偏离也就形成了我们所知的引力。

在牛顿理论中，引力是无中生有的，然而在爱因斯坦的理论中，引力产生于四维流形的内在几何性质中。在流形中伸展更多，或者和直角坐标偏离更大的地方，引力也就更强。有时人们将其称为“橡胶膜物理”。在这种物理模型中，使行星绕着恒星转，恒星绕着星系转的巨大的力，不过是弯曲空间的副产品。引力实际上是几何的作用。

如果在四维空间中可以解释引力的形成，那么五维空间会给我们带来什么科学上的优势呢？为什么不试一试呢？1919年，一个叫卡鲁扎（Theodor Kaluza）的年轻波兰数学家提出了这个问题，他想着既然爱因斯坦将引力整合到了时空中，那么类似的，或许再多加一个维度就可以将电磁力视为时空的几何副产物。所以卡鲁扎在爱因斯坦的方程中又加了一个维度，他很高兴地发现在五维空间中两种力都很好地变成了几何模型的产物。

尽管在数学上这个模型如魔法般的好，但是问题是这个额外的维度似乎并不和任何物理实际相吻合。在广义相对论中，这个第四维度是时间；在卡鲁扎的理论中，第五维度并不是任何你可以指向，看到或者感觉的东西，它只是在数学上存在。甚至爱因斯坦都不愿意接受这个看起来不切实际的创新。他问道，这个维度是什么？它到底在哪？

管子上的蚂蚁

1926年，瑞典物理学家克莱因（Oskar Klein）回答了这个问题，而他的答案看起来像是幻想王国来的。他说，想象你是在一条细长的管子上生活的蚂蚁，你可以前后走而感觉不到脚下这个小的环状的维度。只有你们世界的蚂蚁物理学家们可以用蚂蚁的显微镜来看到这些小的维度。根据克莱因的说法，我们四维时空中的每个点都有一圈像管子一样的额外维度，这一维度太小以至于我们看不见。因为这个维度尺度的数量级比原子都要小很多，我们一直以来都忽略了这个维度也不足为奇。物理学家只有用超级强大的粒子加速器才有希望看到这么小的尺度。

在震惊散去后，物理学家们就被克莱因的想法迷住了，在上世纪四十年代，他们对这一理论进行了进一步发展，理论有了更多的数学细节，同时也加入了量子力学的阐释。不幸的是，这一新的维度的尺度极小，让我们很难想象如何通过实验验证它的存在。克莱因计算出这个小圈的直径只有10^-30厘米。与之相比，氢原子的直径有10^-⁸厘米，所以我们讨论的是一个比最小的原子还要小20个数量级以上的尺度。直至今日，我们都没有任何办法看到如此小的尺度。所以这个想法就逐渐失去了关注。

但是卡鲁扎并不是一个轻言放弃的人。他相信自己第五维度的想法，他也相信理论的重要意义，所以他决定自己做一个实验，实验的项目是游泳。卡鲁扎不会游泳，所以就读了所有能读到的关于游泳的理论。在他感觉自己已经掌握了足够多的理论知识后，他陪着家人去了海边，然后冲进了浪中，惊奇地发现他就这样游了起来。在卡鲁扎看来，这个游泳的实验支持了理论的真实性，尽管他最终没有看到自己心爱的第五维度理论的成功，在六十年代研究弦论的理论工作者又重新拾起了高维空间的工作。

到上世纪六十年代，物理学家们发现了自然界另外的两种力，这两种力都是在亚原子尺度作用的。它们叫做弱核力和强核力，这两种力可以导致一些辐射，也可以将夸克组合在一起形成原子核中的质子和中子。在六十年代末期，随着物理学家开始探索弦论新的方面（将粒子假设为空间中极小的橡皮筋的振动），卡鲁扎和克莱因的想法又重新浮现到了理论工作者的脑海中，他们逐渐开始思考这两种亚原子力是否也可以通过时空的几何性质来描述。

后来证明，为了完全包括这两种力，我们必须在数学描述中再加入另外五个维度。当然，没有任何先验的理由来说明必须有五个维度，同时，这些额外的维度和我们的感官经验没有任何关系。它们只是存在于数学描述中。所以我们就有了弦论中的10维宇宙。10个维度中有4个是大尺度的时空维度（可以通过广义相对论描述），另外有6个额外的“致密”维度（一维用于描述电磁力，5维用于描述核力），这些维度都卷曲在一起，几何结构极其复杂。

物理学家和数学家正在花费大量的精力来理解这些极小的维度的可能形状，并试图找出现实世界中有哪些是与之对应的。技术上来说，这些可能的形式被称之为卡拉比－丘流形，它们可以存在于任何更高的偶数维度的空间中。这些形式奇怪诡异，又精细复杂，它们构成了一个多维空间中抽象的类别。一个穿过它们二维薄片（这几乎是我们所知的最好的可视化方式）可以让人联想到病毒的晶体结构，它们看起来几乎是活的。

○ 穿过卡拉比－丘流形的二维薄片。| 图片来源：维基百科

描述10维空间的弦论方程有很多版本，但是在上世纪九十年代，普林斯顿高等研究院（爱因斯坦的常常出没的地方）的数学家爱德华·威滕（Edward Witten）说明假如我们将空间视为11维，问题就会简单很多。他将这一理论称为M理论，而对“M”到底代表什么讳莫如深。通常人们认为M代表膜的英文membrane，但是也有人认为是“矩阵”（matrix），“大师”（master），“迷”（mystery）或“怪物”（monster）。

5维空间中的一个4维泡泡

迄今为止，我们仍然没有任何证据证明这些额外的维度确实存在，我们仍然像游泳的物理学家一样，梦想着我们没有办法到达的微观世界——但弦论确实是数学本身的一个有力的结论。最近，这一理论的某个24维的版本又取得了进步，显示出了和数学的几大分支之间的相互联系，这也就是说，即使弦论最终在物理上不能取得成功，那也会在纯理论方面得到丰厚的回报。在数学中，24维的空间十分特殊，有很多神奇的事会在其中发生，比如以一种极其优雅的方式将球体堆叠在一起，虽然现实世界却不太可能是24维的。大多数弦论方面的理论工作者认为，对于我们所热爱并居住的世界来说，10维或者11维就足够了。

还有最后一部分的弦论发展值得关注。1999年，丽萨·兰达尔（Lisa Randall，哈佛大学第一位拿到终身教职的女性理论物理学家）和拉曼·桑德鲁姆（Raman Sundrum，一位美籍印度裔粒子理论物理学家）提出了很可能还有一个额外的在宇宙尺度上的维度，这个尺度是由广义相对论描述的。根据他们的“膜”理论（即brane理论，brane是membrane的简称），我们通常认为的宇宙很可能嵌在一个更大的五维空间中，类似于一个超级宇宙。在这个超级空间里，我们的宇宙很可能只是很多共同存在的宇宙中的一个，这些宇宙中的每一个都是5维空间中的一个4维泡泡。

我们很难得知是否能够证实兰达尔和桑德鲁姆的理论。即使这个想法和现代天文学最开始的发展过程有不少相似之处。欧洲人在500年前几乎无法想象我们生活的地球之外的其他“世界”，但是现在我们知道宇宙中存在着数以亿计的围绕着恒星旋转的行星。谁知道是否或许有一天我们的后人会发现数以亿计的其他的宇宙，每一个都有自己独特的时空方程。

理解空间几何结构是科学的一项重大成就之一，但是很有可能物理学家们在这条路上已经走到头了。因为在某种程度上来说，亚里士多德可能是对的，对空间扩展的概念在逻辑上可能确实有问题。尽管相对论有卓越的成就，我们知道它对于空间的描述其实并不是完备的，因为在量子层面上，相对论就会失效。在过去的半个世纪，物理学家一直在尝试将在宇宙尺度上理解的空间和量子尺度上的观测统一起来，但是一直没有成功。现在人们越来越觉得这样的一种统一需要激进的新物理。

正如普林斯顿高等研究院院长罗伯特·戴克格拉夫（Robbert Dijkgraaf）最近所说的，爱因斯坦在发展出广义相对论后，用了余生的大部分时间在尝试“用时空的动力学来构建自然法则，将物理学转化为纯粹的几何。对于爱因斯坦来说，时空很自然地是无限的科学概念分层中‘最基本的一层’。”就像牛顿的世界图像一样，爱因斯坦的世界图像将空间视为最基本的存在，空间是其他一切的舞台，但是在很小的尺度上，当量子性质主导时，相关的物理定律告诉我们，我们习以为常的空间实际上可能不存在。

有些理论物理学家近来产生了这样一种观点，认为空间可能其实只是一种更基本的物理概念的涌现，就像温度就是分子运动的宏观涌现一样。正如戴克格拉夫所说：“现在的观点认为时空并不是开始，而是结果，是复杂量子信息导致的自然结构。”

这种想法的一位主要支持者是加州理工学院的宇宙学家肖恩·卡罗尔（Sean Carroll），他最近说经典空间并不是现实的基本结构之一，并提出我们将四维，10维或11维这些维度如此重视的想法是错的。戴克格拉夫用温度来进行比喻，而Carroll让我们考虑“湿度”，湿度的概念是很多水分子聚集时的一种涌现现象。没有任何一个水分子是湿的，只有你将很多水分子聚集在一起时才能够使用湿度的概念，所以空间是由量子层面更本质的东西涌现出来的。

卡罗尔这样写道，从量子角度来说，宇宙在多于10^{10^100}个维度的数学王国中演化，也就是一万兆兆兆兆兆兆兆兆个零，想象这样大的一个数字几乎是不可能的，与这个数字相比，已知宇宙中所有的粒子数目都显得微不足道。然而这些维度中每一个都是由量子方程描述的数学空间中的独立维度；每一个都是宇宙享有的新“自由度”。

假如笛卡尔知道我们把他的想法延伸了多远，以及“维度”这个简单的词包含的极其复杂内容，他一定会震惊不已。

原文链接：

https://aeon.co/essays/how-many-dimensions-are-there-and-what-do-they-do-to-reality