周志华组最新论文提出“溯因学习”,受玛雅文字启发的神经逻辑机
新智元报道
来源:arXiv
作者:闻菲,刘小芹
【新智元导读】南京大学周志华教授等人在最新的一篇论文中提出了“溯因学习”(abductive learning)的概念,将神经网络的感知能力和符号AI的推理能力结合在一起,能够同时处理亚符号数据(如原始像素)和符号知识。实验中,基于溯因学习框架的神经逻辑机NLM,在没有图像标签的情况下,学会了分类模型,能力远超当前最先进的神经网络模型。作者表示,就他们所知,溯因学习是首个专门为了同时进行推理和感知而设计的框架,为探索接近人类水平学习能力的AI打开了新的方向。
假设你在踢足球,球来了,你把球传给队友,“传球”这一个动作,实际上涉及两种不同的思维过程。
首先,你需要意识到脚下有个球,相当于识别(感知);其次,你需要判断把球传给哪个队友,这是推理的结果——传给A不传给B,是因为A没有人防守,而B被两个人盯着。
在人类的大脑中,感知和推理这两种思维过程无缝衔接,甚至可以同时完成。但是,如今的AI系统还无法做到。在当前的机器学习系统中,感知和推理往往是不兼容的。
为了解决这个问题,南京大学的戴望州、徐秋灵、俞扬和周志华,在他们的论文《使用溯因学习打通神经感知和逻辑推理》(Tunneling Neural Perception and Logic Reasoning through Abductive Learning)中,提出了溯因学习(abductive learning)的概念。
溯因学习(abductive learning)能像人一样归纳推理,结合了神经网络的感知能力和符号AI的推理能力。基于溯因学习提出的神经逻辑机NLM(Neural-Logical Machine),能够同时处理亚符号数据(如原始像素)和符号知识。实验中,NLM仅从原始像素中学会了符号间的逻辑关系,能力远超当前最先进的神经网络模型,也即双向LSTM和DeepMind的可微分神经计算机(DNC)。
作者表示,就他们所知,溯因学习是首个专门为了同时进行推理和感知而设计的框架,为探索接近人类水平学习能力的AI打开了新的方向。
而这项研究的灵感,则来自于考古学家破译玛雅文字的过程。
玛雅文字对于现代人类而言完全是一个谜,直到在19世纪末玛雅文字的数字系统和日历被成功破译。正如历史学家所描述的那样,对玛雅数字的识别来源于一些显示出数学规律的图像。由于玛雅的数字系统是二十进制的,与目前普遍使用的十进制系统完全不同,所以破译这个系统非常艰难。玛雅数字的成功解读反映了两种显著的人类能力:1)视觉上感知图像上单个的字;2)在感知过程中基于数学背景知识进行推理。这两种能力同时作用,相互影响。此外,这两种能力常常被人类潜意识地联系在一起,这是许多现实世界中学习问题的关键。
现代人工智能(AI)系统具有这两种能力,但它们是孤立的。深度神经网络在识别人脸、物体、语音方面取得了惊人的性能;基于逻辑的AI系统在证明数学定理,以及关系推理方面已经达到了人类的水平。然而,识别系统很难在符号形式中利用复杂的领域知识,感知信息很难纳入推理系统,而推理系统通常需要语义层面的知识,这涉及到人类的输入或监督。
即使最新的神经网络模型中,具有增强记忆能力、关注关系的能力和可微分知识表示,但是完全逻辑推理能力仍然是缺失的。为了把感知和推理结合起来,关键是要回答这样一个问题:在一个系统中,感知和推理应该如何相互影响?
破译玛雅象形文字的例子
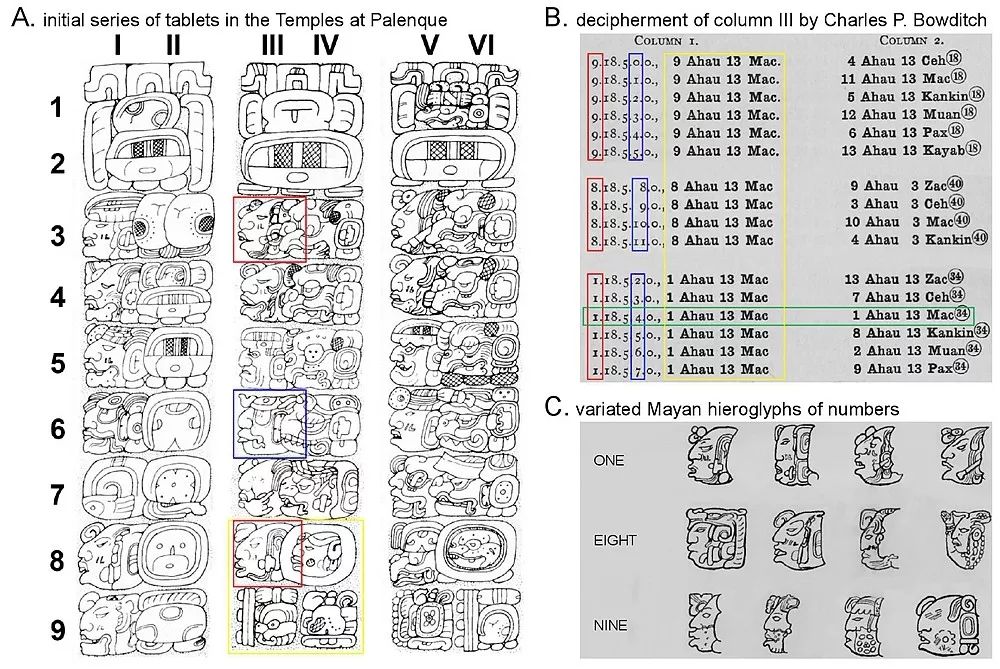
图1:破译玛雅象形文字的图解
为了寻找答案,让我们回到查尔斯 • 鲍迪奇(Charles P. Bowditch)破译玛雅数字的过程,这些玛雅数字被刻成神的头。图1说明了这个过程。图1(A)展示了在帕伦克发现的三片牌碑的部分。第一片(I—II列)使用标准象形文字表示玛雅的时间单位,例如,在II5处的“Tun”(表示“360天”)以及所有三个碑文上的第二行都有这个符号。第四和第六列以完全不同的方式绘制了这些符号,但是鲍迪奇推测,根据它们的位置,它们与第二列意思是一样的。此外,虽然玛雅数字系统是二十进制的,但“Tun”单位只是其前一个单位“Winal”(所有偶数列的第6行)的18倍,这使解密更加困难。
鲍迪奇通过计算和评估这些碑文之间关系的一致性来验证这一点。然后,他开始解读第III列的数字。如图1(B)所示,通过将象形符号映射到不同的数字,然后根据数学规则检查这些数字是否一致, 鲍迪奇最终对这些数字进行了解码并证明了它们的正确性。
这个解决问题的过程被查尔斯·皮尔斯(Charles S. Peirce)称为“溯因”(abduction),司马贺(Herbert A. Simon)称其为“Retroproduction”。它指的是根据背景知识有选择地推断某些事实和假设以解释现象和观察的过程。在鲍迪奇破译玛雅数字这一过程中,背景知识包括算术、关于玛雅历法的一些基本事实;假设包括一个将象形符号映射为有意义的符号的识别模型,以及对玛雅历法系统的更全面的理解。最后,通过反复试验和一致性检查来确保假设的有效性。
受到人类的溯因问题解决过程的启发,作者提出了“Abductive Learning”框架,该框架使机器学习中感知能力和推理能力的结合得以实现。
一般来说,机器学习是一个在大的假设空间中搜索一个最优模型的过程。约束条件被用来缩小搜索空间。大多数机器学习算法利用数学公式显式表达的约束。但是,就像解码玛雅语言时要使用其他领域的知识一样,现实世界的任务中,许多复杂的约束都是以符号规则的形式表示的。而且,这种象征性的知识可能是不完整的,甚至是不准确的。Abductive Learning使用逻辑溯因来处理不完美的符号推理问题。如果把领域知识写成一阶的逻辑规则,那么Abductive Learning就可以外展(abduce)多种假设来作为观察到的事实的可能解释,正如鲍迪奇在“尝试”这个步骤中,基于他对算术和玛雅语言的知识来对这些未知的象形文字进行猜测。
传统的基于逻辑的AI为了利用一阶逻辑规则写成的领域知识,根据输入的逻辑基础,使用规则进行逻辑推理,所推理的是领域内对象之间关系的逻辑事实。事实上,这隐含地假设了对象和关系的绝对存在。然而,正如斯图尔特·罗素(Stuart Russell)评论的那样,“现实中的物体很少会带有独特的标识符,也不会像演出剧本那样预先宣布它们的存在”。因此,溯因学习利用神经感知自动从数据中提取符号;然后,逻辑溯因被应用于神经感知的一般化结果。
溯因学习的关键是要发现逻辑溯因(logical abduction)和神经感知(neural perception)可以怎样同时训练。当一个可微的神经感知模块被耦合到一个非可微的逻辑溯因模块时,学习系统的优化就变得非常困难:因为传统的基于梯度的方法不适用了。与鲍迪奇解码玛雅文字类似,溯因学习使用启发式试错搜索方法(heuristic trial-and-error search approach)来结合这两个功能。
逻辑溯因作为一个离散的推理系统,可以很容易地处理一组符号输入。感知模块的神经层应当输出使符号假设彼此一致的符号。当假设不一致时,逻辑溯因模块从神经感知模块中发现不正确的输出,并对其进行纠正。这个过程就是鲍迪奇在图1(B)中所遵循的试错过程。校正函数作为监督信号来训练神经感知模块。
为了验证溯因学习的有效性,作者实现了一个神经逻辑机( Neural Logical Machine ,NLM)来演示这个溯因学习框架。图2展示了一个用于分类手写等式的NLM的架构。分类手写等式就是让机器从一组标记好的等式中学习,训练好的模型可以正确地预测未来的等式。这个任务与破译玛雅象形文字十分类似:机器没有提前知道象形文字或计算规则的含义,并且需要同时使用感知和推理。
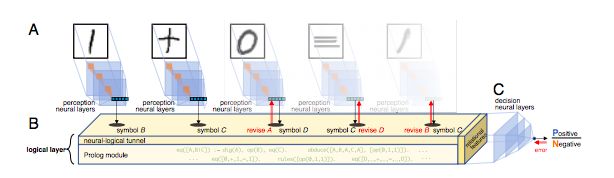
图2:神经逻辑机(NLM)的架构。(A)感知神经层(例如卷积层)完成感知任务。(B)感知层的结果用作逻辑层的输入,由神经逻辑通道,Prolog模块和关系特征组成。Prolog模块用于检查输入一致性并生成关系特征; 神经逻辑通道根据与假设的一致性来校正感知输出;关系特征揭示了逻辑过程的结果。(C)决策神经层将关系特征转换成最终输出。
启发式试错法搜索(heuristic trial-and-error search)是在神经逻辑通道中使用无梯度优化( derivative-free optimization)实现的。尽管逻辑层可以发现逻辑规则和感知符号之间的不一致性,但是它不能找到错误符号的位置。
NLM采用无梯度的优化方法来猜测符号出现错误的位置。对每一个猜测,Prolog模块运行溯因逻辑程序(abductive logical programming,ALP),以确定正确的符号出现在指定的位置,使逻辑假设更加一致。我们通过在每次训练迭代期间仅提供可用训练数据的样本来进一步加速NLM。从数据集样本中,只能得到局部一致的假设。最后,NLM使用命题式技术(propositionalization technique)将局部一致的假设转化为关系特征。
作为一个人类解决问题过程的类比,NLM的工作方式如下:在训练之前,将提供给第一级逻辑程序的领域知识提供给Prolog模块。训练开始后,训练数据样本将被解释为在神经逻辑通道中预定义的候选原语符号。由于感知神经层最初是一个随机网络,解释的符号通常是错误的,形成不一致的假设。逻辑层开始修改解释的符号并在训练数据样本中搜索最一致的逻辑假设。假设作为关系特征存储在逻辑层中,而符号修正用于以直观的监督方式训练感知神经层。
当这两个子部分的训练完成时(例如感知层收敛或达到迭代限制),NLM再次处理所有训练样本以获得溯因的关系特征的特征向量。最后,决策神经层用这些来自整个数据集的特征向量进行训练。决策神经层的学习过程将自动过滤不良感知神经层、假设和关系特征。此外,由于象征溯因的高度复杂性,我们采用课程学习(curriculum learning)的范式来训练NLM(即从更简单的例子开始学习,学习任务的难度逐渐增加。)
为了验证神经逻辑机NLM的性能,作者进行了手写等式识别(Handwritten Equations Decipherment)和任务迁移(Cross-task Transfer)两项实验。
在手写等式识别任务中,输入是图像,包括手写的数字“0”、“1”,符号“+”、“=”,以及外观类似的符号“≈”、“∝”,系统需要从样例像素中学习符号之间的逻辑关系,然后判断测试集中的等式是否成立。
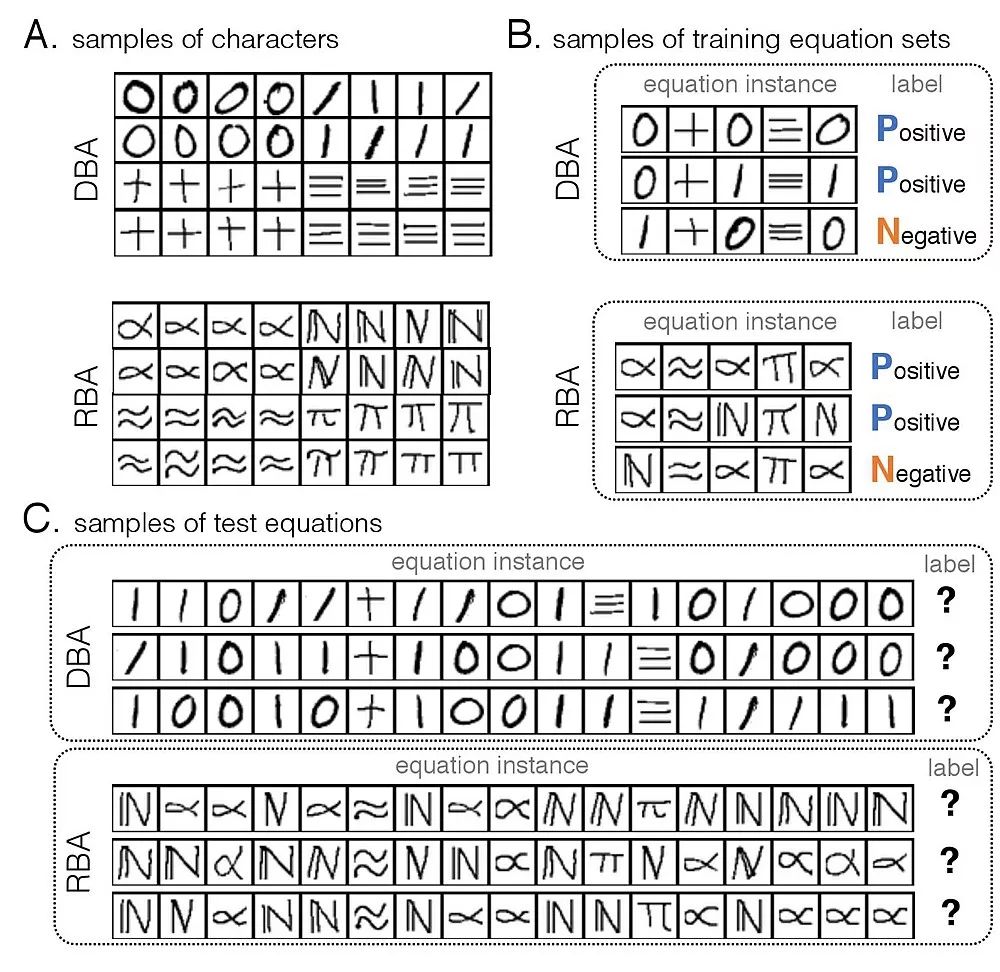
图3:A和B是样例,系统需要从A和B中学习符号之间的关系,其中,A是手写数字及符号;B是训练集,有标签,表明成立(P)或不成立(N)。C是测试集,测试集并没有标签。
作者将NLM的性能与当前最先进的双向LSTM(BiLSTM)和可微分神经计算机DNC相比较,因为后两者都能够解决序列输入问题,而且是当前的最高基准。尤其是DNC,由于外接存储器,在符号计算方面展示了很强的潜力。
结果发现,NLM性能要显著优于两者,并且使用了更少的训练样本。不仅如此,当测试集的公式变长时,BiLSTM和DNC性能快速下降,而NLM却成功维持了超过80%的正确率。作者表示,这体现了一种接近人类水平的学习能力。
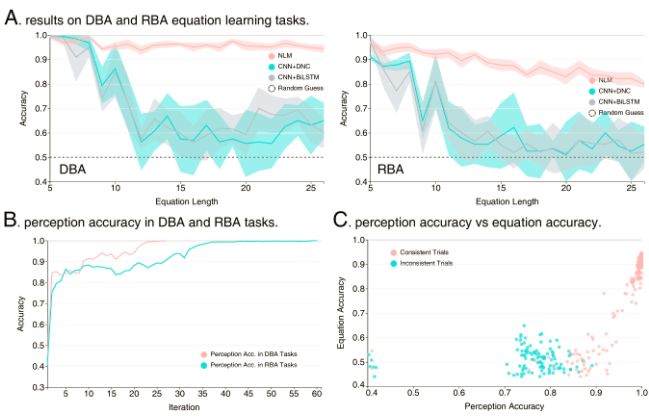
图4:图A是NLM与其他方法在手写公式识别上的结果。红色代表NLM,随着公式长度增加(从5个字符到25个),NLM的准确性一直保持在80%以上,但是,DNC(蓝色)和BiLSTM(灰色)下降明显。
作者还检测了在NLM内部,随着学习的增加,感知精度有所提高(上图B)。这一结果表明,逻辑上的一致性可以充当监督信号。
此外,感知能力(图像识别性能)能够促进NLM在分类公式时的准确性(上图C)。
任务迁移(Cross-task Transfer)实验则验证了NLM在知识迁移上的性能。详情参见论文。
受Bowditch解密玛雅文字的反复试错试验启发,溯因学习将符号推理与表示感知连接起来,得益于一阶逻辑的表达力,还能直接利用通用的领域知识。
作者表示,他们还将继续改进和完善溯因学习框架,让AI系统自己学习背景知识,并且让学到的知识能在其他任务中重用,更进一步接近人类水平的学习能力。
论文地址:https://arxiv.org/pdf/1802.01173.pdf
加入社群
新智元AI技术+产业社群招募中,欢迎对AI技术+产业落地感兴趣的同学,加小助手微信号: aiera2015_1 入群;通过审核后我们将邀请进群,加入社群后务必修改群备注(姓名-公司-职位;专业群审核较严,敬请谅解)。
此外,新智元AI技术+产业领域社群(智能汽车、机器学习、深度学习、神经网络等)正在面向正在从事相关领域的工程师及研究人员进行招募。
加入新智元技术社群 共享AI+开放平台