会员服务 ·

2022年最新3篇GNN领域综述！

2022 年 2 月 18 日 机器学习与推荐算法

嘿，记得给“机器学习与推荐算法”添加星标

本文分享3篇关于图神经网络（GNN）的相关综述：

第1篇是对联邦图神经网络的调研，将目前的工作根据三层分类法进行了划分，即根据数据的原始存在形式、联邦学习的常规设置进行了分类介绍；

第2篇文献则是对几何等变图神经网络的调研，其根据GNN中的消息传递和聚合方式将现有的方法分为三类进行介绍；

第3篇文献则是对异质图神经网络的调研。

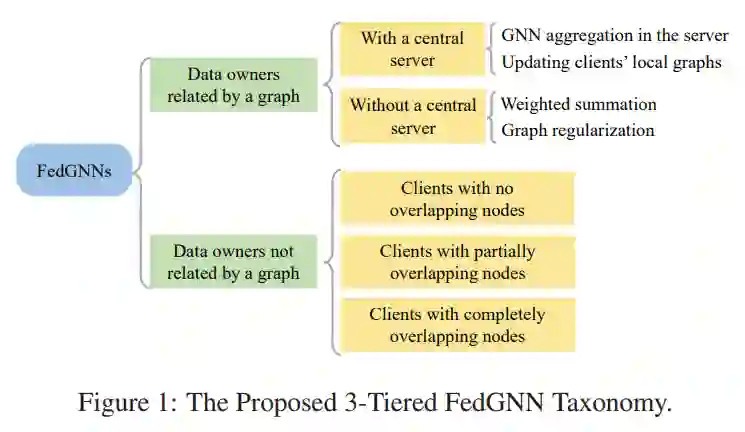
1. Federated Graph Neural Networks: Overview, Techniques and Challenges.

论文地址：https://arxiv.org/pdf/2202.07256

摘要：

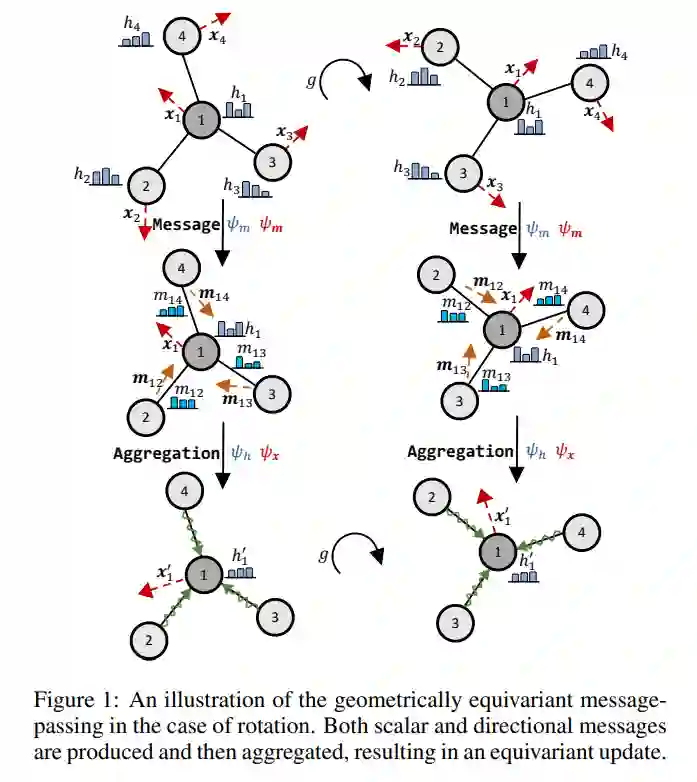
图神经网络在实际应用中具有强大的数据处理能力，因此受到了广泛的关注。然而，随着社会越来越关注数据隐私，GNN面临着适应这种新常态的需要。这导致了近年来联邦图神经网络(Federated Graph Neural Network，简称FedGNNs)研究的迅速发展。尽管这一跨学科领域前景广阔，但对感兴趣的研究人员来说具有很高的挑战性。在这个话题上缺乏有见地的调研只会加剧这个问题。

在这篇论文中，我们通过提供这一新兴领域的全面调研来弥补这一差距。我们提出了关于FedGNN文献的一个独特的三层分类法（如图1所示），以提供一个清晰的视角来了解GNN在联邦学习(FL)环境中是如何工作的。它通过分析图数据如何在FL设置中表现自己，如何在不同的FL系统架构下进行GNN训练，如何在不同的数据竖井中进行图数据重叠程度，以及如何在不同的FL设置下进行GNN聚合，将现有的工作纳入视野。通过对现有工作的优势和局限性的讨论，我们展望了未来的研究方向，可以帮助构建更健壮、动态、高效和可解释的联邦图神经网络。

2. Geometrically Equivariant Graph Neural Networks: A Survey.

论文地址：https://arxiv.org/pdf/2202.07230

摘要：

许多科学问题都要求以几何图形的形式处理数据。与一般图形数据不同，几何图形展示了平移、旋转和/或反射的对称性。研究人员利用这种归纳偏差，开发了几何等变图神经网络(GNN)，以更好地表征几何图形的几何和拓扑。尽管取得了丰硕的成果，但仍缺乏对等变GNN进展的综述，这反过来阻碍了等变GNN的进一步发展。为此，基于必要而简明的数学基础，我们根据GNN中的消息传递和聚合的表示方式，将现有的方法分为三类。我们也总结了基准和相关的数据集，以便于以后的研究，为方法学的发展和实验评估。并对未来可能的发展方向进行了展望。

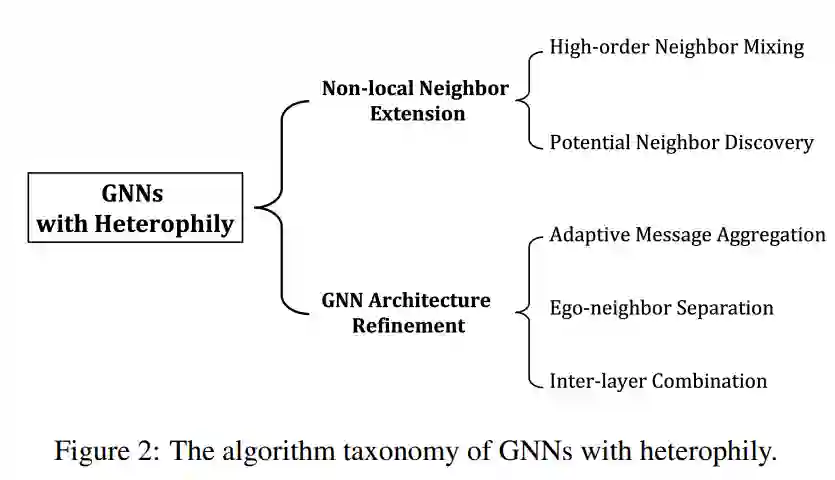
3. Graph Neural Networks for Graphs with Heterophily: A Survey.

论文地址：https://arxiv.org/pdf/2202.07082

摘要：

近年来，图神经网络(GNN)得到了迅速的发展，为无数的图分析任务和应用提供了便利。一般来说，大多数GNN依赖于同质性假设，即属于同一类的节点更有可能被连接。然而，作为现实世界众多场景中普遍存在的图属性，异质性(即具有不同标签的节点往往被链接)严重限制了定制同质GNN的性能。因此，GNN for Heterophilic Graphs在这个社区中得到了越来越多的关注。据我们所知，本文首次对异质图的gnn作了一个全面的综述。具体来说，我们提出了一个系统的分类法，该分类法本质上支配着现有的亲异GNN模型，并对其进行了一般性的总结和详细的分析。此外，我们总结了主流的异亲图基准，以促进稳健和公平的评估。最后，我们指出了在异亲图研究和应用方面的潜在发展方向。