图神经网络入门（一）GCN图卷积网络

2020 年 4 月 29 日 专知

本文是清华大学刘知远老师团队出版的图神经网络书籍《Introduction to Graph Neural Networks》的部分内容翻译和阅读笔记。
个人翻译难免有缺陷敬请指出，如需转载请联系翻译作者
作者：Riroaki
原文：https://zhuanlan.zhihu.com/p/129305050

第一部分-Introduction

图是一种数据结构，可对一组对象（节点）及其关系（边）进行建模。近年来，由于图的强大表达能力，利用机器学习来分析图的研究受到越来越多的关注，即图可以用作包括社会科学（社会网络）在内的各个领域的大量系统的表示图是一种数据结构，可对一组对象（节点）及其关系（边）进行建模。

作为用于机器学习的独特的非欧氏数据结构，图引起了人们对节点分类，链接预测和聚类分析的关注。图神经网络（GNN）是在图域上运行的基于深度学习的方法。由于其令人信服的性能和高解释性，GNN最近已成为一种广泛应用的图形分析方法。

首先，GNN是由卷积神经网络（CNN）启发的。CNN能够提取和组合具有高表示能力的特征的多尺度局部空间特征，这导致了几乎所有机器学习领域的突破和深度学习的革命。CNN的关键在于：本地连接，共享权重和多层使用。这些特点对于解决图域问题也非常重要，因为

图是最典型的局部连接结构；
与传统的频谱图理论相比，共享权重降低了计算成本；
多层结构是处理分层模式的关键，它捕获了各种大小的特征。

但是，CNN只能对诸如图像（2D网格）和文本（1D序列）之类的常规欧几里得数据进行操作，这些数据也可以视为图的实例，但是很难定义局部卷积滤波器和池化运算符以应用于一般的图结构。

另一个动机来自图嵌入（Graph Embedding），它旨在学会表示图节点，边缘或低维向量中的子图。在图分析中，传统的机器学习方法通常依赖于手工设计的特征，并且受其灵活性和高成本的限制。继表示学习的思想和词嵌入的成功以来，DeepWalk被认为是基于表示学习的第一种图嵌入方法，它采用了SkipGram模型。诸如node2vec，LINE和TADW等类似方法也取得了突破。然而，这些方法具有两个严重的缺点。

编码器中的节点之间没有共享参数，这导致计算效率低下，因为这意味着参数的数量随节点的数量线性增长；
直接嵌入方法缺乏泛化能力，这意味着它们无法处理动态图或无法泛化为新图。

第二部分-Vanilla Graph Neural Networks

在图结构中，一个节点自然是由其特征和图中的相关节点定义的。GNN的目标是为每个节点学习节点的状态嵌入的状态，该状态对邻域信息进行编码。状态嵌入用于产生输出，例如预测节点标签的分布。原始GNN模型处理无向齐次图，其中图中的每个节点都有其输入特征，每条边也可能都有其特征。本文使用和来表示节点的边和邻居的集合。

为了根据输入邻域更新节点状态，定义一个在所有节点之间共享的参数函数，称为局部转移函数。为了产生节点的输出，有一个参数函数，称为局部输出函数。然后，定义为：

对于节点，分别表示节点特征、节点连接的边的特征、节点的邻居的隐藏状态和节点邻居的特征。

如果将所有的状态、输出、特征和节点特征分别堆叠起来并使用矩阵表示为：，那么上面的公式可以改写为：

其中分别是全局的转移和输出函数，由所有节点的对应函数堆叠构成。的值是等式（3）的不动点，并以作为压缩映射（Contraction Map）唯一定义。因而，在实践中通过迭代方式求出。这里，的计算过程可以用前馈神经网络（Feedforward Neural Network）来解释。

以上是GNN的基本框架。下面介绍如何学习转移函数和输出函数的参数。
利用用于监督信号的目标信息（对于特定节点记为），损失函数可以写为：

于是整个基于梯度下降的学习算法可以描述为如下步骤：

隐藏状态通过迭代时间步获得，然后我们获得公式（3）一个近似的不动点解；

通过损失函数计算梯度，并使用最后一步计算得到的梯度更新网络参数。

该模型的局限之处在于：

迭代更新节点的隐藏状态以获取固定点的计算效率低下。该模型需要步计算才能逼近固定点。如果放宽固定点的假设，可以设计一个多层GNN来获得节点及其邻域的稳定表示。
模型在迭代中使用相同的参数，而大多数流行的神经网络在不同的层中使用不同的参数，这是一种分层的特征提取方法。此外，节点隐藏状态的更新是一个顺序过程，可以从RNN核（如GRU和LSTM）中受益。
图的边上还有一些信息特征，无法在模型中有效地建模。例如，知识图中的边具有关系的类型，通过不同边的消息传播应根据其类型而不同。此外，如何学习边缘的隐藏状态也是一个重要的问题。
如果很大，那么如果我们专注于节点的表示而不是图本身，则不宜使用固定点，因为固定点的表示分布会更平滑，并且在区分每个节点时信息量也较小。

基于以上不足，部分变种模型被提出：比如门控图神经网络（Gated GNN）解决了第一个不足，关系图神经网络（Relational GNN）解决有向图的问题。部分网络在后文中会提及。

第三部分-Graph Convolutional Networks

图神经网络旨在将卷积推广到图领域。在这个方向上的进展通常分为频谱方法（Spectral Method）和空间方法（Spatial Method）。

频谱方法（Spectral Method）

首先介绍Spectral Network。通过计算图拉普拉斯算子的特征分解，在傅立叶域中定义卷积运算。可以将操作定义为信号（每个节点的标量）与由参数化的滤波器的乘积：

其中是由归一化的拉普拉斯矩阵的特征向量组成的矩阵：，其中分别是度矩阵和邻接矩阵。该操作会导致潜在的密集计算和非空间局部过滤器。

这里我也不太理解，什么叫做“ non-spatially localized ﬁlters”？暂时翻译为非空间局部过滤器，后续再作补充。

第二个要介绍的是ChebNet。这个模型使用K阶切比雪夫多项式（Chebyshev Polynomials）来近似：

其中，表示最大的特征值。是切比雪夫多项式的系数向量。可以看出，该模型是K-邻域（K-localized）的，因为它是近似的阶多项式。通过引入切比雪夫多项式，ChebNet不必计算拉普拉斯矩阵的特征向量，降低了计算量。

切比雪夫多项式的定义：

接下来正式介绍GCN。通过限制层级的卷积为来缓解了节点度分布非常宽的图对局部邻域结构的过度拟合问题，并进一步近似，可以将（2）简化为：

其中是两个不受约束的变量。我们添加约束使得，则得到：

注意到如果直接堆叠这个运算，将会导致数值不稳定和梯度的爆炸或者消失问题，引入重归一化（Renormalize）：，其中，最终进行堆叠可以得到对于任意通道的信号和个特征映射的滤波器的定义：

其中，是滤波器组参数成的矩阵，是卷积得到的信号矩阵。
此时的GCN作为一个谱方法的简化，也可以看作是一种空间方法。

最后介绍AGCN（Adaptive GCN）。以上所有的模型均使用原始图结构表示节点之间的关系。然而，不同节点之间可能存在隐式关系，于是有人提出了自适应图卷积网络（AGCN）以学习底层关系。AGCN学习一个“残差”图并将其添加到原始拉普拉斯矩阵中：

其中，是超参数，可以通过一个学习到的邻接矩阵计算得到：

自适应量度背后的想法是，欧氏距离不适用于图结构化数据，并且该量度应适应任务和输入特征。AGCN使用广义的Mahalanobis距离：

其中也是一个学习得到的矩阵，满足，是迁移空间的转移基底矩阵（transform basis），然后AGCN计算高斯核函数并将G归一化以获得邻接矩阵：

空间方法（Spatial Method）

在上述所有频谱方法中，学习的滤波器都取决于拉普拉斯的特征基向量，而后者取决于图的结构。这意味着在特定结构上训练的模型不能直接应用于具有不同结构的图。

空间方法与频谱方法相反，直接在图上定义卷积，在空间上相邻的邻居上进行运算。空间方法的主要挑战是定义大小不同的邻域的卷积运算并保持CNN的局部不变性。

Neural FPS。对度不同的节点，使用不同的权重矩阵：

其中，是度为的节点在第层对应的权重矩阵，表示在节点的相邻节点的集合，是节点在第层对应的嵌入。可以从（10）中看出，模型首先将节点与它相邻节点的嵌入做累加，并使用进行变换。对于度不同的节点，模型定义不同的权重矩阵。模型的主要不足在于不能应用在大规模图结构中，因为它的节点具有很多不同的度。

Patchy-SAN。首先，为每个节点精确选择并归一化k个邻居。然后，将归一化的邻域用作接受域（receptive ﬁled）作卷积运算，试图将图学习问题转化为常规的欧氏几何数据的学习问题。该方法具有四个步骤（如下图所示）：

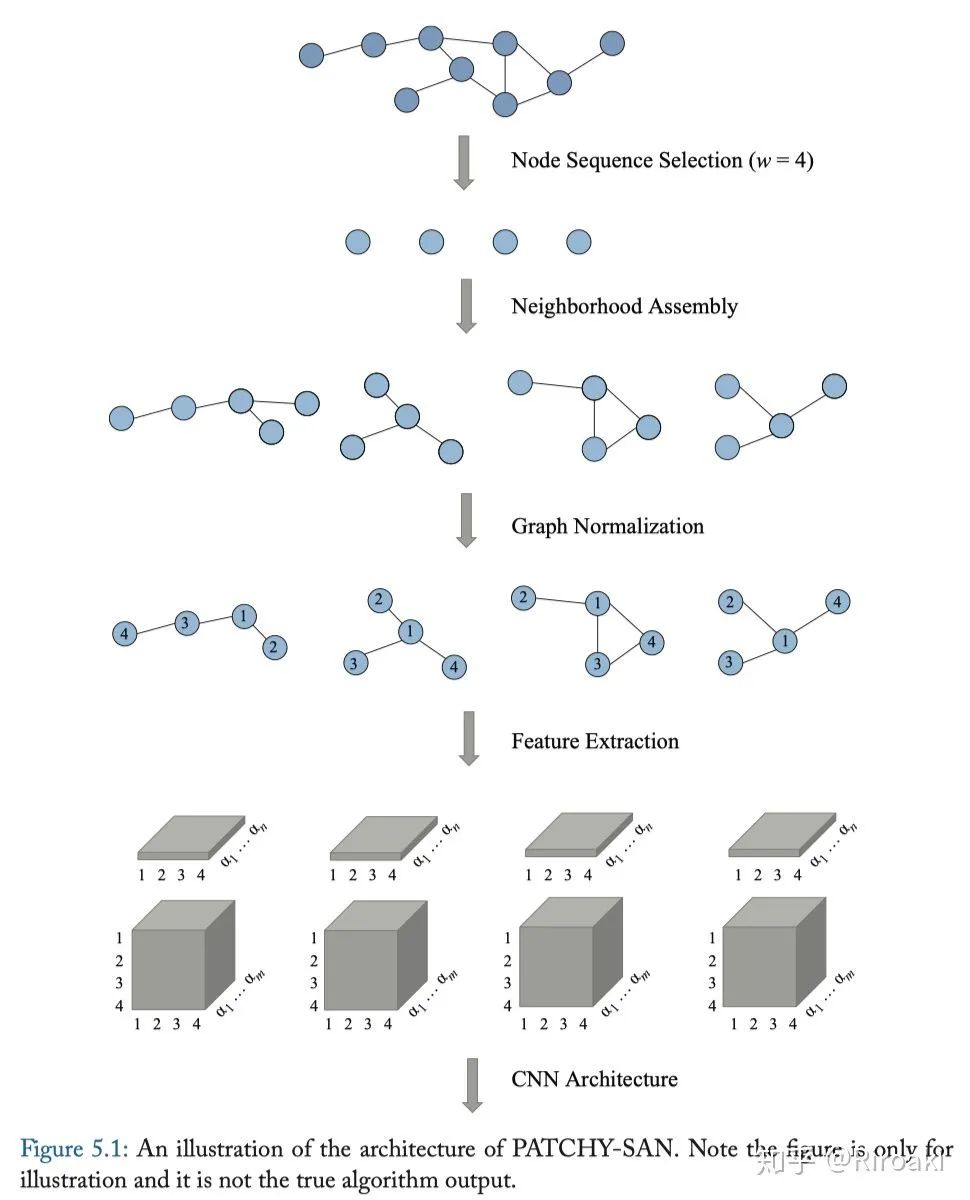
节点序列选择。此方法无法处理图中的所有节点，二是选择要处理的节点序列。首先，使用图形标注过程来获取节点的顺序和节点序列。然后，该方法使用步长从序列中选择节点，直到选择了个节点。
相邻节点聚合。在这一步中，构造了从第一步中选择的节点的接受域。每个节点的邻居都是候选者，模型使用简单的广度优先搜索为每个节点收集k个邻居。
图归一化。在这一步中，该算法旨在给接受域中的节点一个顺序，以便从无序图空间映射到矢量空间。这是最重要的步骤，它背后的想法是为不同的图中的两个具有相似的结构地位的节点分配相似的相对位置。
卷积结构。在归一化后，可以使用CNN进行卷积。归一化的邻域用作接受域，节点和边属性被视为通道。

DCNN（Diﬀusion-Convolutional Neural Networks）。转移矩阵用于定义DCNN中节点的邻域。

对于节点分类问题，模型定义：

其中是输入特征（是节点个数，是特征维度），，是图邻接矩阵的节点度归一化的转移矩阵。每一个实体都转化为通过在维特征上经过跳图扩散计算的的扩散卷积表示（diﬀusion convolutional representation）。然后经过权重的点乘和非线性激活函数，得到了每个节点的表示。

这里我个人翻译非常不通顺，其实描述的就是公式（11）里说的……

对于图分类问题，DCNN将每个节点的表示求出平均值，即：

其中，表示维的全1向量。

DCNN也可以应用于边分类任务，此时需要将边改为点并增广邻接矩阵。

这里原文是converting edges to nodes and augmenting the adjacency matrix.，我不太理解“边改成点”具体是什么意思，保留疑问。

DGCN（Dual GCN）同时考虑图上的局部一致性和全局一致性。它使用两个卷积网络来捕获局部/全局一致性，并采用无监督的损失来聚合两个部分。模型结构如下图：

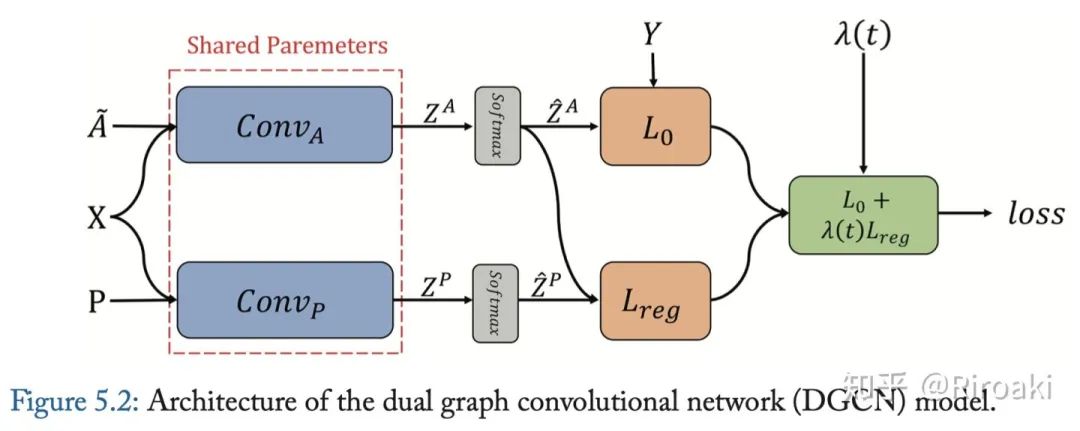
第一个卷积网络与等式（5）相同。第二个网络用正点向互信息（PPMI，positive pointwise mutual information）矩阵替换邻接矩阵：

其中是PPMI矩阵，是的对角度矩阵，是非线性激活函数。结合使用两种观点的动机是：

式（5）对局部一致性进行建模，这表明附近的节点可能具有相似的标签；
式（13）对全局一致性进行建模，它假设具有相似上下文的节点可能具有相似的标签。局部一致性卷积和全局一致性卷积分别称为。

然后将两个卷积结果聚合：

其中是调节两部分损失的动态权重，是用节点标签的有监督损失。如果我们的预测包含种标签，用表示输出的矩阵和输出后经过softmax的矩阵，那么有：

其中是训练数据下标的集合，是真实标签。

的计算为：

其中表示经过softmax的输出。因此，是衡量两个卷积输出距离的无监督损失函数。

LGCN（Learnable GCN）。该网络基于可学习图卷积层（LGCL）和子图训练策略。LGCL利用CNN作为聚合器。它对节点的邻域矩阵进行最大池化，以获取前k个要素元素，然后应用1-D卷积来计算隐藏表示。计算过程如下图：

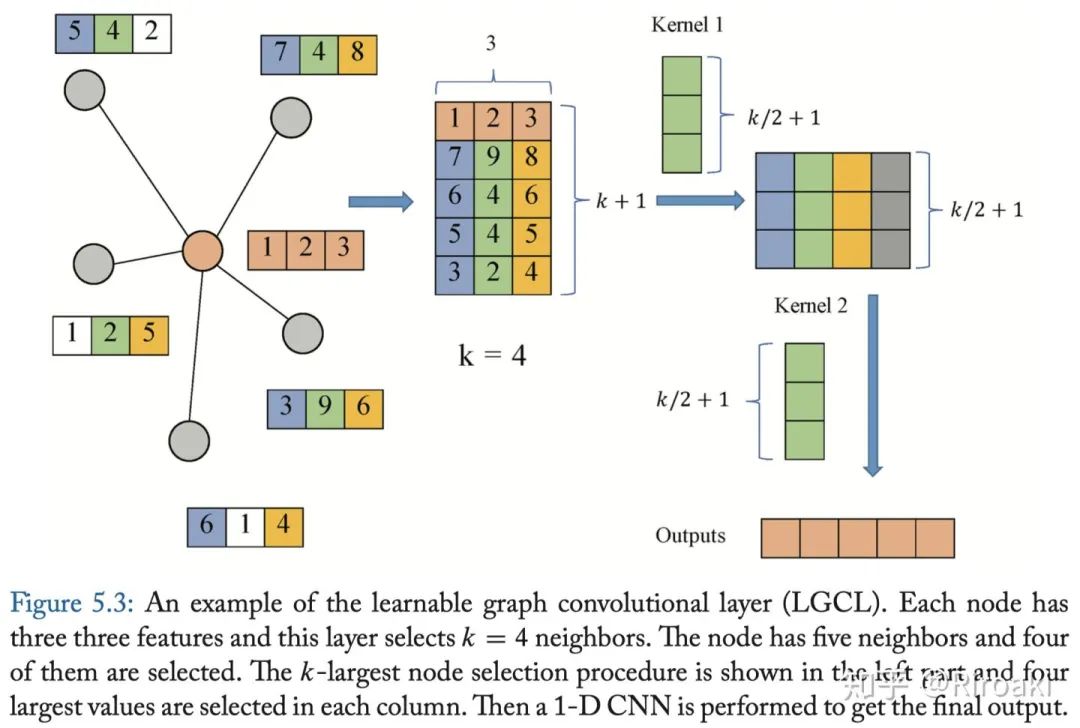
LGCL的传播步骤公式如下：

其中是邻接矩阵，是选取最大的个节点的操作，表示常规的一维CNN。该模型使用个最大的节点选择操作来收集每个节点的信息。对于给定的节点，首先收集其邻居的特征。假设它具有个邻居，并且每个节点具有个特征，则获得矩阵。如果，则用零列填充。然后选择第个最大的节点，即将每一列中的值排序并选择前个值。之后，节点的嵌入插入的第一行将得到矩阵，并进行1-D卷积来聚合特征。卷积函数的输入维度为，输出维度为。

MoNeT。提出了模型GCNN（Geodesic CNN）、ACNN（Anisotropic CNN）、GCN、DCNN的泛化形式。

使用表示节点，表示节点相邻的一个节点，MoNet计算伪坐标（pseudo-coordinates），并对不同相邻节点使用不同权重：

其中，模型需要学习的参数为，表示相邻节点个数。接着就可以定义卷积：

对于上面提到的不同方法，都可以看作这种形式，只不过它们的有所区别，如下表：

GraphSAGE。该模型是一个泛化的inductive框架，通过采样和聚合邻居节点的特征来产生节点的嵌入。传播过程为：

其中，是第层的参数。

然而，GraphSAGE并不使用所有的相邻节点。，二是随机采样固定数量的相邻节点，AGGREGATE步骤可以有多种形式，包括：

平均聚合（Mean aggregator）。可以看作是近似版本的transductive GCN卷积操作，inductive GCN的变体写作：这个聚合方法和其他方法不同之处在于不像（20）中那样进行拼接操作，可以被看作是一种残差连接（skip connection），所以效果更好。
LSTM聚合（LSTM aggregator）。基于LSTM实现，具有更高的表达能力，但是由于建模序列数据，所以不同的排列会造成不同的结果。可以通过修改LSTM的实现来对无序的相邻节点集合作处理。
池化聚合（Pooling aggregator）。将邻节点的嵌入通过一个全连接层并最大池化：，这里的池化也可以用任意对称的计算替代。