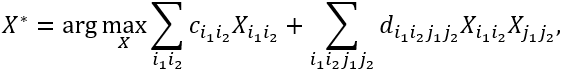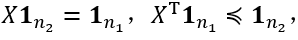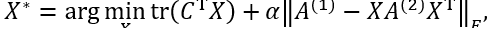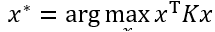AI综述专栏 | 非精确图匹配方法综述
AI综述专栏简介
在科学研究中,从方法论上来讲,都应先见森林,再见树木。当前,人工智能科技迅猛发展,万木争荣,更应系统梳理脉络。为此,我们特别精选国内外优秀的综述论文,开辟“综述”专栏,敬请关注。
作者简介
王涛,北京交通大学计算机与信息技术学院副教授,主要研究方向为机器学习与计算机视觉。于2013年在北京交通大学计算机学院获博士学位,2014至2015年赴美国天普大学计算机系访问学习。近年来在TPAMI、CVIU、AAAI、ECCV等期刊和会议上发表论文多篇。
凌海滨,1997年和2000年于北京大学分别获得学士和硕士学位,2006年在美国马里兰大学获博士学位,2006至2007年在加州大学洛杉矶分校从事博士后研究。2000至2001年任微软亚洲研究院助理研究员,2007至2008年任西门子研究院研究员。从2008起任职于美国天普大学(Temple University),现在为计算机系终身教授。自2014年起同时担任亮风台信息科技首席科学家。主要研究领域为计算机视觉、增强现实、医学图像分析和人机交互。获2003年度ACM UIST最佳学生论文奖,2014年度美国自然科学基金CAREER Award。担任期刊IEEE Trans. on Pattern Analysis and Machine Intelligence (PAMI),Computer Vision and Image Understanding (CVIU),和Pattern Recognition的编委(Associate Editor),以及计算机视觉领域顶级会议CVPR 2014、CVPR 2016和CVPR 2019年的领域主席(Area Chair)。
摘要
图匹配问题,尤其是允许属性和结构差异的非精确图匹配问题,是计算机科学领域的一个经典问题。该问题的难度在于目标函数的非凸性以及解空间的离散性。近几十年来,研究者们为提高算法的匹配性能和计算效率进行了坚持不懈的努力,取得了可观的进展。本文将对近期非精确图匹配问题的主要动向进行简要的分析和梳理,并展望未来工作。
一. 引言
图结构是计算机领域最常用的复杂模式表示方法之一,许多模式识别领域的应用问题都可以形式化表示为图匹配问题。给定两个图,图匹配涉及建立它们的顶点集之间的对应关系,并同时考虑边集之间的一致性。
基于图结构的模式匹配不是一个孤立问题,而是相关问题的一个集合。其范围涵盖了从图同构判别问题(在该问题中匹配严格遵从于图结构),到在数以百万计的以属性图表示的复杂模式中寻找非精确匹配。大部分具有重要实践意义的图匹配问题都具有很高的复杂性。子图同构问题已被证明为NP完全问题[1],图同构问题既没有被证明为NP完全问题,也没有人提出一个多项式算法能够解决此问题[2]。
在许多实际应用中,特别是在机器学习和模式识别领域,外部噪声的存在使得来自于表示同一类模式的不同图之间可能存在不同程度的差异。因此,相对于精确图匹配问题,考虑图之间的结构和标签差异的非精确图匹配问题引起了更多研究者的兴趣。本文主要对非精确图匹配问题的研究现状进行分析和梳理,并展望未来工作。
二. 问题描述
一个带有n个节点的图可以表示为一个二元组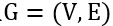
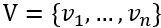
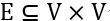
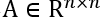
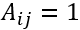
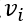
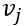
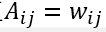
给定两个图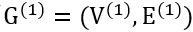
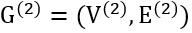
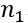
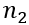
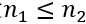
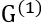
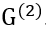
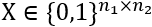
其中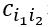
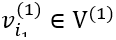
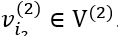
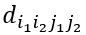
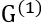
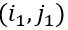
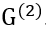
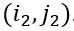
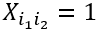
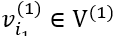
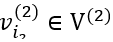
其中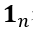
若用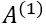
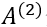
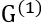
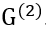
其中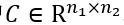
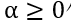
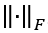
由于赋权图中每条边只关联一个标量属性,上述的赋权图匹配模型在实践中有很大限制。在近期的研究中,一个更加通用的图匹配模型表示为
其中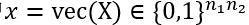
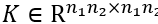
其中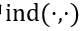
三. 非精确图匹配方法研究现状
图匹配是计算机科学中的一个经典问题,其研究历史已经超过四十年,但依然没有得到很好的解决。该问题的难点在于目标函数的非凸性和解空间的离散性,使得人们无法在有效的时间内寻找到一个全局最优解。鉴于此,目前的研究主要集中在如何在有效的时间内寻找一个可接受的近似解或者局部最优解。
3.1基于函数松弛的方法
图嵌入方法:
图嵌入方法主要是通过利用一些嵌入方法(流形嵌入、谱嵌入)等技术将图的顶点映射到特征空间,然后利用特征空间的点集匹配方法,如半正定规划、聚类等,实现特征空间中的顶点的匹配,来近似地完成图顶点的匹配。
作为一个早期的代表性工作,Umeyama[3]提出了正交约束下的图匹配问题的一种松弛表示形式,并通过利用邻接矩阵的谱得到该松弛问题的全局最优解。该解法的非负性往往不能保证,因此需要进一步利用离散化过程得到最终的匹配解。另外,该方法只能够处理相同大小的图匹配问题。Luo等[4]提出基于最大期望算法(EM)和奇异值分解理论(SVD)的结构图匹配方法。该方法能够实现不同大小的图的匹配,且具有较强的优化理论支撑。Caelli等[5]提出一种基于图的邻接矩阵谱嵌入方法的匹配算法。该方法首先将图的顶点嵌入到由其邻接矩阵的谱空间,然后利用聚类算法实现谱空间中的顶点的匹配,进而间接实现了一种图的顶点匹配过程。Bai等[6]首先利用流形学习的方法把待匹配的结构图的顶点嵌入到低维欧式空间,然后利用半正定规划优化方法实现在低维欧式空间中点集之间的匹配。该方法从优化角度上不能保证匹配解的优化性,但操作简单,在实际应用中具有很强的实用性。Tang等[7]提出一种图顶点的嵌入与匹配的协同表示框架,通过协同考虑图的顶点嵌入与匹配过程,提出了更加一般的基于联合嵌入模型的图匹配方法。考虑到图谱多议性对图匹配精度的影响,Feng等[8]提出采用一个多议矩阵对图谱多议性进行建模,随后通过对多议矩阵和置换矩阵的交替优化来解决图匹配问题。
除了上述基于谱嵌入的方法,等距嵌入[9,10]、子模式嵌入[11-13]、原型嵌入[14-16]等方法皆可用于将图节点嵌入到高维特征空间,进而将图匹配问题转换为特征空间中的点集匹配问题。
二部图匹配:
不同于一般的图匹配,二部图匹配(BGM)方法仅考虑优化过程中的局部边缘结构[17],而不需要获取图之间的全局一致性。这种方法的主要思想是通过将局部边缘结构编码为单个节点,将图形编辑距离的难题转换为线性分配问题。在这种方法中允许插入,删除和替换节点和边缘,但是这些编辑操作以相互独立的方式处理。随后,Serratosa[18]提出了快速二部图匹配算法,它获得了与[17]完全相同的距离值和节点之间的匹配结果,而运行效率显著提高。但是,该快速算法在一些特定的代价矩阵存在不收敛的问题。鉴于此,该作者随后提出一个新的快速算法[19],通过定义新的代价矩阵来解决原算法可能不收敛的问题。另一方面,Riesen等[20]通过融合不同的搜索策略来提高二部图匹配方法的精度。团图匹配方法[21,22]可以看作是二部图匹配方法的变体,它将各个节点的局部邻接结构编码成团,然后采用二部图匹配方法完成团之间的匹配。方法[22]于[21]的主要区别在于采用稀疏子空间聚类方法来发现邻居节点并构造团。考虑到二部图匹配方法仅获得精确图形编辑距离的近似解,Riesen和Ferrer提出了一项有趣的工作,来预测训练分类器对各个节点分配的正确性[23],预期预测结果将被结合到匹配过程或后处理过程中以便改进匹配结果。
二部图匹配算法通过对节点局部结构信息进行编码,将图编辑距离转换为线性分配问题来获得高计算效率,但是全局结构的缺失通常会损害其匹配精度。
3.2基于约束松弛的方法
连续优化:
由于图匹配本质上是离散优化问题,因此一类典型的策略是将其松弛到连续域,如此很多成熟的优化方法可以用于获得一个连续域上的最优解,然后重新将其投影到离散域中。
一个显著的工作是Leordeanu等[24]提出的基于谱松弛的方法。该方法建立一个新的分配关系图,其节点表示潜在的匹配关系,其边的权重表示潜在匹配关系之间的成对一致性。通过计算分配关系图的亲和力矩阵(affinitymatrix)的主特征向量获得该松弛模型的全局最优解。但该方法的在匹配过程中忽略了一对一匹配约束性,因而解的性能通常较差。随后,Cour等[25] 在两个方面扩展了这项工作:其一是是将一对一或一对多映射约束(表示为仿射约束)编码到频谱分解,另一是在亲和力矩阵上应用双原型归一化,以显着减少匹配误差并提高整体匹配性能。Cho等[26]提出与[24]中类似的分配关系图,将给定两个图之间的匹配关系作为关联图中的节点排序和选择问题进行搜索,并引入一种保持亲和力的随机游走算法,以基于其准静态分布来驱动节点排序。对于整数二次规划(IQP)公式,该算法与[24]中的算法等效。Jiang等[27]提出了一种拉格朗日松弛匹配方法,首先通过拉格朗日松弛的方式将匹配问题的双随机约束嵌入到优化的匹配目标函数中,然后利用多元乘子优化的方法实现对松弛模型的求解。
除了上述基于矩阵优化的方法之外,概率论方法也常常被用来解决图匹配问题。Christmas等[28]提出了一种概率松弛下的图匹配模型与算法。Zass等[29]提出了超图匹配的概率框架,通过引入超边权重矩阵与所需的节点到节点概率匹配之间的代数关系,形式化了问题输入和输出的软匹配标准。在该框架下,通过迭代连续投影算法获得匹配标准的全局最优。Caelli等[30,31]从概率图模型角度对图匹配模型进行重新表示,并研究利用概率推理算法实现对图匹配问题的求解。随后,Zhang等[32]同样将图匹配问题的求解转化为图模型中的推理问题,并提出了一种新的推理算法实现图匹配问题的求解。.Cho等[33]在贝叶斯概率框架下提出了一种渐进图匹配方法,通过概率投票的方式实现对匹配关系的渐进扩展,从而最终获得更加准确的图匹配结果。Egozi等[34]将谱松弛和概率框架合并在一起,其中谱匹配方案[24]被解释为赋值概率在两个假设下的最大似然估计。作者通过进一步放宽这些假设,提出一种新的概率匹配算法。
上述这些基于连续域优化的算法在优化过程中放弃了的图匹配问题的离散约束,因此需要后投影步骤来将连续域的解离散化。它们所采用的离散化通常独立于匹配的目标函数,因此可能导致弱优化的解决方案。
渐进投影:
鉴于上述连续优化算法的后投影过程存在的与目标函数无关的问题,许多重要的算法对约束松弛和离散化策略进行重新设计,将优化求解和后投影步骤纳入统一框架。
Gold等[35]采用渐进匹配技术,使用泰勒展开迭代求解成本函数的一系列线性近似,从而得到最终问题的解。随后,Tian等[36]进一步分析了该渐进匹配方法的收敛性,并基于此提出了一种新的渐进匹配方法。Leordeanu等[37]提出了一种整数定点投影算法来优化整数域中的目标函数,该算法可采用任何连续或离散解决方案作为输入。随后,Lu等[38]通过利用双随机投影方法开发出更有效的定点投影算法。
近几年一项突出的工作是称为“路径流”的图匹配算法。Zaslavskiy等[38]将图匹配重新描述为凸凹松弛过程(CCRP)问题,然后通过在两个更简单的松弛函数(凸松弛和凹松弛)之间进行插值来求解。该算法从初始凸松弛函数的最优解出发,通过逐步提高插值目标函数的非凸性从而渐进地将初始解投影到离散空间获得最终解。随后,Liu等[39]将该路径流算法从无向图扩展到有向图。遵循类似的策略,Zhou等[40,41]将亲和矩阵分解为较小矩阵的Kronecker积,分解矩阵分别对图的节点亲和度以及边亲和度进行编码,并提供基于分解矩阵的特定凸、凹松弛函数。之后,Liu和Qiao[42]提出了渐进式非凸凹过程(GNCCP),并证明它等效地实现了部分置换矩阵的CCRP。 GNCCP为CCRP提供了一种更简单的实现方法,无需明确地涉及特定的凸、凹松弛函数。
最近,Wang等[43]针对“路径流”这一类图匹配算法共同存在的计算复杂度较高的问题,提出了基于自适应路径估计的路径流算法。该算法通过动态估计每次迭代的初始解并自适应地调整迭代步长,能显著地提高路径流算法的计算效率。另一方面,针对路径流算法中存在的奇点问题,Wang等[44]提出分支路径流算法。该算法通过对初始路径进行奇点检测,并在奇点处搜索不同的路径分支以寻找更好的解,以提高图匹配问题最终解的性能。随后,Wang等[45]对前述两个算法进行有机结合,提出了自适应分支路径流算法,在计算效率和解性能两个维度对原有路径流算法进行了提升。
稀疏模型:
图匹配问题的最优解是离散的、二元的,因此本质上是稀疏的。稀疏约束匹配方法旨在通过放弃离散约束而增加稀疏约束来获得匹配问题的一个稀疏优化解。稀疏可以看作是离散的一种近似,因此稀疏解可以看作是一种近似离散解。
最近的研究开发了一些图匹配选择问题的稀疏优化模型。这些稀疏匹配模型的主要思想是尝试在L1范数下优化特征匹配(匹配选择)目标约束并且可以为问题生成稀疏解决方案,从而通过使用解决方案的非零条目自然地进行匹配选择。例如,从游戏理论的角度来看,Albarelli等[46,47]提出了匹配具有单纯形(非负L1范数)约束的模型。该模型通常用于许多匹配任务[48],但该方法的稳定性较差。Jiang等[49]提出了一种基于Lp范数稀疏约束的图匹配模型。相比于L1范数,Lp范数往往能够获得更加稳定的匹配效果。随后,Jiang等[50]进一步研究了一种基于L12范数的局部稀疏约束的匹配模型。相比于之前的稀疏匹配模型,L12局部稀疏模型更多地考虑到匹配问题的匹配约束性。Rodol`a等人[51]从回归分析的角度对图匹配这一QAP问题进行了解释,提供了现有稀疏约束方法与完善的正则化技术之间的自然联系。该方法通过在两个有效组合上引入加权参数来控制准确性/稀疏性之间的权衡,进而从变量选择的角度给出了一组新约束,通过引入弹性网约束(L1和L2范数的线性组合)代替L1范数约束,并进一步提供了弹性网络匹配模型。
然而,通过这些算法获得的解决方案的稀疏性通常是不可控制的,因此通常还需要后离散化步骤来保证获得最终的离散解决方案。
3.3基于离散搜索的方法
除了上述基于目标函数松弛或约束松弛的近似求解策略,最近,研究者提出了一些纯粹的离散方法来直接在离散空间中搜索解。这些方法可以生成遵循离散仿射映射约束的解决方案,因此不需要任何后优化步骤。
Lee等[52]提出数据驱动的马尔可夫链蒙特卡罗(DDMCMC)框架,通过利用图亲和矩阵的谱特性来解决一般图匹配问题。该方法采用MCMC框架和数据驱动的状态转换建议,有效地探索了图匹配的解空间。Suh等人[53]提出一种基于序列蒙特卡罗(SMC)框架的鲁棒图匹配算法,设计了一系列人工目标分布,其提供从初始分布到最终目标分布的平滑过渡作为图匹配目标。该算法通过精巧设计的重要性分布和重采样方案,在一对一匹配约束下有效地探索解空间。Yan等人[54]提出了超图匹配的离散方法。该方法采用迭代过程将高阶指派问题近似为一阶线性指派问题。在每次迭代中,采用梯度分配方法(例如匈牙利方法)进行离散优化,以在整数域中找到最优分配矩阵。这种“离散”求解器相对于“软匹配”方法省去了启发式后舍入步骤,在实验中展现了其计算性能上的优势。随后,Yan等人在[55]中理论上证明了该方法的收敛性,设计了一种自适应松弛机制,确保提出的离散方法在适当的条件下收敛于一个固定解。Adamczewski等人[56]将图匹配问题转化为相应关联图的等效加权最大团问题,提出了软鼓励的惩罚关联图框架,直接在离散解空间中搜索满足一对一约束的解。其于上述框架,采用禁忌搜索作为优化技术,利用搜索历史在寻找最优解的同时做出更多战略决策,从而在一定程度上避免陷入局部最优解。
基于离散搜索的方法绕过了上面提到的解空间松弛问题,但是它们的搜索通常是有限而低效的,因为一对一的匹配约束显著地限制了这些方法中可能的移动。因而,离散搜索方法的最优性通常是难以保证的,很大程度上取决于算法的初始化。
四. 未来研究展望
正如前所述,图匹配问题的难点主要在于目标函数的非凸性以及解空间的离散性。尽管有关图匹配方法的研究已经持续了几十年,并且取得了实质性的成果,但依然有很多问题有待进一步研究。
在图匹配问题中,语义和结构哪个更重要?如何融合语义相似性和结构相似性以产生一致的匹配?例如,如果图G1和G2在结构上相似,但具有不同的属性值,而G1和G3具有相似的属性值,但在结构上有所不同,G2和G3中哪一个更适合G1?
现有图匹配算法的结果都严重依赖于图中节点和边的属性选择以及相似性(或距离)度量的定义。这些属性和度量的选择通常适用于特定的约束或有限的应用。因此,研究学习更加适合匹配任务的属性、度量以及亲密矩阵对实现高效的匹配具有十分重要的作用。最近,Zanfir等[57]提出基于深度学习的图匹配方法,为这方面的研究提供了一个新的思路。
由于图匹配问题的复杂性,目前研究者提出了许多近似算法,但是这些算法大都具有较高的计算复杂性,所适用的图的规模依然十分有限。而在社交网络、脑网络、智能网格等领域,图的节点数达到数以万计甚至百万计,研究开发更加快速的图匹配算法具有更加实际的应用价值.
在许多应用问题中,如多源传感器数据分析,类似的对象不是单独或成对出现,而是频繁地以集合形式出现。给定一组具有相同或相关结构的图,多图匹配问题涉及在所有图中找到一组一致的匹配。相对于两图匹配,多图匹配问题的研究远不成熟,有待进一步地深入研究。
参考文献
[1]. M. Garey, D. Johnson,Computers and intractability - A guide to the theory of NP-completeness.Freeman and Company, 1979.
[2]. J. Kobler, U.Schoning, J. Toran, The graph isomorphism problem: Its structural complexity.Boston: Birkhauser, 1993.
[3]. S. Umeyama. An eigendecomposition approach to weighted graph matching problems. IEEE Trans. PatternAnal. Mach. Intell., 1988, 10(5):695—703.
[4]. B. Luo,E. R. Hancock. Structural graph matching using the EMalgorithm and singular value decomposition. IEEE Trans. Pattern Anal. Mach.Intell., 2001, 23(10):1120-1136.
[5]. T. Caelli,S. Kosinov. An eigenspace projection clustering methodfor inexact graph matching. IEEE Trans. Pattern Anal. Mach. Intell., 2004, 26(4):515-519.
[6]. X. Bai,E. R. Hancock,R. C. Wilson. A generative model for graph matching and embedding.Computer Vision and Image Understanding, 2009, 113(7):777—789.
[7]. J. Tang, B. Jiang, A.Zheng, B. Luo. Graph matching based on spectral embedding with missing value.Pattern Recognition, 2012, 45(10): 3768-3779.
[8]. W. Feng, Z. Liu, L.Wan, C. Pun and J. Jiang. A spectral-multiplicity-tolerant approach to robustgraph matching. Pattern Recognition 2013, 46(10): 2819-2829.
[9]. E. Bonabeau. Graphmultidimensional scaling with self-organizing maps. Inf. Sci. 2002, 143(1-4):159-180.
[10]. S. Jouili, S.Tabbone. Graph Embedding Using Constant Shift Embedding. In ICPR, 2010, pp.83-92.
[11]. M. M. Luqman, J.Ramel, J. Lladós and T. Brouard. Fuzzy multilevel graph embedding. PatternRecognition, 2013, 46(2): 551-565.
[12]. J. Gibert, E. Valvenyand H. Bunke. Dimensionality Reduction for Graph of Words Embedding. In GbRPR,2011, pp. 22-31.
[13]. J. Richiardi, D. V.De Ville, K. Riesen and H. Bunke. Vector Space Embedding of Undirected Graphswith Fixed-cardinality Vertex Sequences for Classification. ICPR, 2010, pp.902-905.
[14]. K. Riesen, M. Neuhausand Horst Bunke. Graph Embedding in Vector Spaces by Means of PrototypeSelection. In GbRPR, 2007, pp. 383-393.
[15]. K. Riesen and H.Bunke. Graph Classification by Means of Lipschitz Embedding. IEEE Trans.Systems, Man, and Cybernetics, Part B, 2009, 39(6): 1472-1483.
[16]. E. Z. Borzeshi, M.Piccardi, K. Riesen and H. Bunke. Discriminative prototype selection methodsfor graph embedding. Pattern Recognition, 2013, 46(6): 1648-1657.
[17]. K. Riesen and H.Bunke. Approximate graph edit distance computation by means of bipartite graphmatching. Image Vision Computation, 2009, 27(7): 950–959.
[18]. F. Serratosa. Fastcomputation of bipartite graph matching. Pattern Recognition Letters, 2014,45:244–250.
[19]. Francesc Serratosa.Speeding up Fast Bipartite Graph Matching Through a New Cost Matrix. IJPRAI,2015, 29(2).
[20]. K. Riesen, H. Bunke:Improving bipartite graph edit distance approximation using various searchstrategies. Pattern Recognition, 2015, 48(4): 1349-1363.
[21]. V. Carletti, B.Gaüzère, L. Brun, M. Vento. Approximate Graph Edit Distance ComputationCombining Bipartite Matching and Exact Neighborhood Substructure Distance. InGbRPR, 2015, pp. 188-197.
[22]. W. Nie, A. Liu, Z.Gao, and Y. Su. Clique-graph matching by preserving global & localstructure. In CVPR, 2015, pp. 4503–4510.
[23]. K. Riesen and M.Ferrer. Predicting the correctness of node assignments in bipartite graphmatching. Pattern Recognition Letters, 2016, 69:8–14.
[24]. M. Leordeanu and M.Hebert. A spectral technique for correspondence problems using pairwiseconstraints. In ICCV, 2005, pp. 1482–1489.
[25]. T. Cour, P.Srinivasan, and J. Shi. Balanced graph matching. In NIPS, 2006, pp. 313–320.
[26]. M. Cho, J. Lee, andK. M. Lee. Reweighted random walks for graph matching. In ECCV, 2010, pp.492–505.
[27]. B. Jian,T. Tang,X. Cao and B. Luo.Lagrangian relaxation graph matching. Pattern Recognition,2017,61: 255—265.
[28]. W. J. Christmas, J.Kittler and M. Petrou. Structural Matching in Computer Vision Using ProbabilisticRelaxation. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17(8): 749-764.
[29]. R. Zass and A.Shashua. Probabilistic graph and hypergraph matching. In CVPR, 2008.
[30]. Terry Caelli, TibérioS. Caetano. Graphical models for graph matching: Approximate models and optimalalgorithms. Pattern Recognition Letters, 2005, 26(3): 339-346.
[31]. Tibério S. Caetano,Terry Caelli, Dale Schuurmans, Dante Augusto Couto Barone. Graphical Models andPoint Pattern Matching. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28(10):1646-1663.
[32]. Z. Zhang, Q. Shi, J.J. McAuley, W. Wei, Y. Zhang and A. van den Hengel. Pairwise Matching throughMax-Weight Bipartite Belief Propagation. In CVPR, 2016, pp. 1202-1210.
[33]. M. Cho, K. M. Lee.Progressive graph matching: Making a move of graphs via probabilistic voting.CVPR, 2012, pp. 398-405.
[34]. A. Egozi, Y. Keller,and H. Guterman. A probabilistic approach to spectral graph matching. IEEETrans. Pattern Anal. Mach. Intell., 2013, 35(1):18–27.
[35]. S. Gold and A. Rangarajan. A graduated assignmentalgorithm for graph matching. IEEE Trans. Pattern Anal. Mach. Intell., 1996,18(4):377–388.
[36]. M.Leordeanu, M. Hebert, and R. Sukthankar. An integer projected fixed pointmethod for graph matching and MAP inference. In NIPS, 2009, pp. 1114–1122.
[37]. Y. Lu,K. Huang, and C. Liu. A fast projected fixed-point algorithm for large graphmatching. Pattern Recognition, 2016, 60:971–982.
[38]. M.Zaslavskiy, F. R. Bach, and J. Vert. A path following algorithm for the graphmatching problem. IEEE Trans. Pattern Anal. Mach. Intell., 2009, 31(12):2227–2242.
[39]. Z. Liu,H. Qiao and L. Xu: An Extended Path Following Algorithm for Graph-MatchingProblem. IEEE Trans. Pattern Anal. Mach. Intell., 2012, 34(7): 1451-1456.
[40]. F. Zhouand F. D. la Torre. Factorized graph matching. In CVPR, 2012, pp. 127–134.
[41]. F. Zhouand F. D. la Torre. Factorized graph matching. IEEE Trans. Pattern Anal. Mach.Intell., 2016, 38(9):1774–1789.
[42]. Z. Liuand H. Qiao. GNCCP - graduated nonconvexityand concavity procedure. IEEE Trans.Pattern Anal. Mach. Intell., 2014, 36(6):1258–1267.
[43]. T. Wangand H. Ling. Path following with adaptive path estimation for graph matching.In AAAI, 2016, pp. 3625–3631.
[44]. T. Wang,H. Ling, C. Lang, and J. Wu. Branching path following for graph matching. InECCV, 2016, pp. 508–523.
[45]. T. Wang,H. Ling, C. Lang, and S. Feng. Graph Matching with Adaptive and Branching PathFollowing. IEEE Trans. Pattern Anal. Mach. Intell., 2018.
[46]. A.Albarelli, S. R. Bulò, A. Torsello, and M. Pelillo. Matching as anon-cooperative game. In ICCV, 2009, pp. 1319–1326.
[47]. A.Albarelli, E. Rodola, and A. Torsello. Imposing semi-local geometricconstraints for accurate correspondences selection in structure from motion: agame-theoretic perspective. International Journal of Computer Vision, 2012,97(1): 36–53.
[48]. E. Rodolà,A. M. Bronstein, A. Albarelli, F. Bergamasco, and A. Torsello. A game-theoreticapproach to deformable shape matching. In CVPR, 2012, pp. 182–189.
[49]. B.Jiang, J. Tang, B. Luo, and L. Lin. Robust feature point matching with sparsemodel. IEEE Trans Image Process, 2014, 23(12): 5175–5186.
[50]. B.Jiang, J. Tang, C. Ding, B. Luo. A Local Sparse Model for Matching Problem. InAAAI, 2015, pp. 3790-3796.
[51]. E.Rodol`a, A. Torsello, T. Harada, Y. Kuniyoshi, and D. Cremers. Elastic netconstraints for shape matching. In ICCV, 2013, pp. 1169–1176.
[52]. J. Lee,M. Cho, and K. M. Lee. A graph matching algorithm using data-driven markovchain monte carlo sampling. In ICPR, 2010, pp. 2816-2819.
[53]. Y. Suh,M. Cho, and K. M. Lee. Graph matching via sequential monte carlo. In ECCV,2012, pp. 624-637.
[54]. J. Yan,C. Zhang, H. Zha, W. Liu, X. Yang, and S. M. Chu. Discrete hyper-graphmatching. In CVPR, 2015, pp. 1520–1528.
[55]. J. Yan,C. Li, Y. Li, and G. Cao. Adaptive Discrete Hypergraph Matching. IEEE Trans.Cybernetics, 2018, 48(2): 765-779.
[56]. K.Adamczewski, Y. Suh, and K. M. Lee. Discrete tabu search for graph matching. InICCV, 2015, pp. 109–117.
[57]. A.Zanfir and C. Sminchisescu. Deep learning of graph matching. In CVPR, 2018, pp.1-8.
@ CAA-PRMI专委会通讯
版权声明
本文版权归《CAA-PRMI专委会通讯》,转载请自行联系。
历史文章推荐: