图神经网络还能这样学，看新加坡小哥圈圈画画搞掂GNN（免费赠书）

选自medium

作者：Rishabh Anand

机器之心编译

参与：Panda

在社交网络分析等一些应用中，图神经网络已经得到了广泛的应用。新加坡科技研究局（A*STAR）的研究者 Rishabh Anand 近日通过图解的方式介绍了图与图神经网络的基本概念，或许能帮助初学者更直观地理解图神经网络的内涵和价值。此外，为了满足读者们对图神经网络的学习需求，机器之心联合极验团队向读者们赠送 20 本《深入浅出图神经网络：GNN 原理解析》，欢迎大家积极留言获得赠书。

图深度学习（Graph Deep Learning，GDL）是一个很有发展前景的研究领域，基于图数据来学习和分析非常有用。 本文将介绍简单图神经网络（GNN）的基础知识及其内在工作原理背后的直观知识 。不过，大家不用担心，为了能够更直观地看懂究竟发生了什么，作者在文中使用了大量彩图给出图解信息。

图（Graph）是什么？

图是一种由连接在一起的节点（顶点）和边构成的数据结构，可用于表示没有明确起点或终点的信息。所有节点都可占据空间中的任意位置，当用二维或多维空间绘制图的结构时，具有相似特征的节点通常会聚集到一起。

这就是一个图，由一群分别表示实体的互连节点构成。

边上面的黑色尖头表示节点之间的关系类型，其可表明一个关系是双向的还是单向的。 图有两种主要类型：有向图和无向图 。在有向图中，节点之间的连接存在方向；而无向图的连接顺序并不重要。有向图既可以是单向的，也可以是双向的。

图可以表示很多事物——社交网络、分子等等。节点可以表示用户/产品/原子，而边表示它们之间的连接 ，比如关注/通常与相连接的产品同时购买/键。社交网络图可能看起来像是这样，其中节点是用户，边则是连接：

节点表示用户，边则表示两个实体之间的连接/关系。真实的社交网络图往往更加庞大和复杂！

接下来作者会介绍一些概念，如循环单元、嵌入向量表征和前馈神经网络。知道一些有关图论的知识（比如什么是图以及图的形态）也很不错。

有些术语你可能并不熟悉。不用担心！对于那些让人疑惑的术语，作者都尽力链接了他可以找到的最靠谱的解释，能让你理解所涉概念的基本含义。基于此，你还能进一步了解这些概念，同时还能理解它们在图神经网络中所发挥的作用。

了解图神经网络

每个节点都有一组定义它的特征 。在社交网络图的案例中，这些特征可以是年龄、性别、居住国家、政治倾向等。每条边连接的节点都可能具有相似的特征。这体现了这些节点之间的某种相关性或关系。

假设我们有一个图 G，其具有以下顶点和边：

这个图与上图是一样的。

为了简单起见，我们假设其特征向量是当前节点的索引的 one-hot 编码。类似地，其标签（或类别）可设为节点的颜色（绿、红、黄）。那么这个图看起来会是这样：

节点的顺序其实并不重要。

注：在实际运用中，尽量不要使用 one-hot 编码，因为节点的顺序可能会非常混乱。相反，应该使用可明显区分节点的特征，比如对社交网络而言，可选择年龄、性别、政治倾向等特征；对分子研究而言可选择可量化的化学性质。

现在，我们有节点的 one-hot 编码（或嵌入）了，接下来我们将神经网络引入这一混合信息中来实现对图的修改。所有的节点都可转化为循环单元（或其它任何神经网络架构，只是我这里使用的是循环单元）；所有的边都包含简单的前馈神经网络。那么看起来会是这样：

其中的信封符号只是每个节点的 one-hot 编码的向量（嵌入）。

消息传递

一旦节点和边的转化完成，图就可在节点之间执行消息传递 。这个过程也被称为「近邻聚合（Neighbourhood Aggregation）」，因为其涉及到围绕给定节点，通过有向边从周围节点推送消息（即嵌入）。

注：有时候你可为不同类型的边使用不同的神经网络，比如为单向边使用一种神经网络，为双向边使用另一种神经网络。这样你仍然可以获取节点之间的空间关系。

就 GNN 而言，对于单个参考节点，近邻节点会通过边神经网络向参考节点上的循环单元传递它们的消息（嵌入）。参考循环单位的新嵌入更新，基于在循环嵌入和近邻节点嵌入的边神经网络输出的和上使用循环函数。我们把上面的红色节点放大看看，并对这一过程进行可视化：

紫色方块是一个应用于来自近邻节点的嵌入（白色信封）上的简单前馈神经网络；红色三角形是应用于当前嵌入（白色信封）和边神经网络输出（黑色信封）之和上的循环函数，以得到新的嵌入（最上面的白色信封）。

这个过程是在网络中的所有节点上并行执行的，因为 L+1 层的嵌入取决于 L 层的嵌入。因此，在实践中，我们并不需要从一个节点「移动」到另一节点就能执行消息传递。

注：边神经网络输出（黑色信封）之和与输出的顺序无关。

最后的向量表征有什么用？

执行了几次近邻聚合/消息传递流程之后，每个节点的循环单元都会获得一组全新的嵌入。此外，经过多个时间步骤/多轮消息传递之后，节点对自己和近邻节点的信息（特征）也会有更好的了解。这会为整个图创建出更加准确的表征。

要进一步在该流程的更高层面上进行处理或者只是简单地表征该图，你可以将所有嵌入加到一起得到向量 H 来表示整个图。

使用 H 比使用邻接矩阵更好，因为不管怎样对图进行扭转变形，这些矩阵都并不表征图的特征或独特性质——只是节点之间的边连接（这在某些情形下并不是很重要）。

总结一下，我们将所有节点循环单元的最终向量表征加到一起（当然，与顺序无关），然后使用所得到的向量作为其它工作过程的输入或简单地将其用于表征该图。这个步骤看起来如下图所示：

这是经过 n 次重复消息传递之后带有已完全更新的嵌入向量的最终图。你可以将所有节点的表。征加到一起得到 H。

四步骤助你实现图神经网络

GNN 用起来相当简单。事实上，实现它们涉及到以下四个步骤：

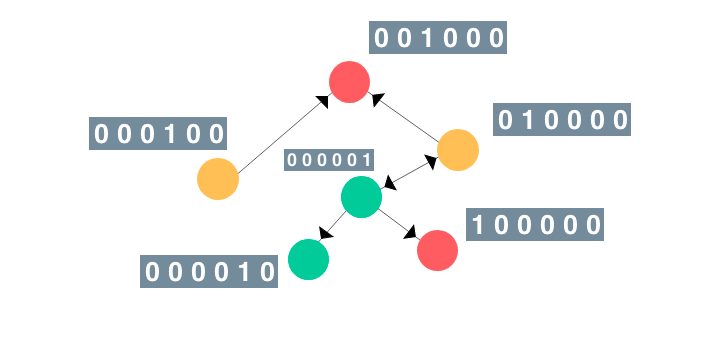
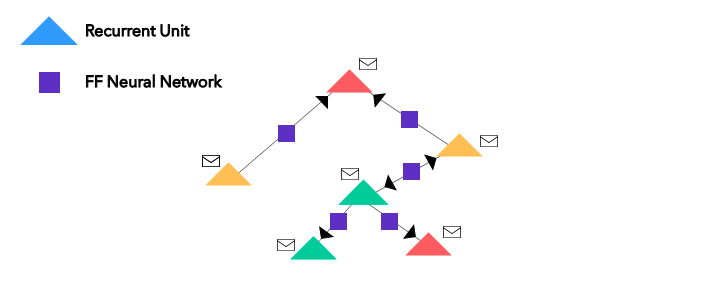
1. 给定一个图，首先将节点转换为循环单元，将边转换为前馈神经网络；

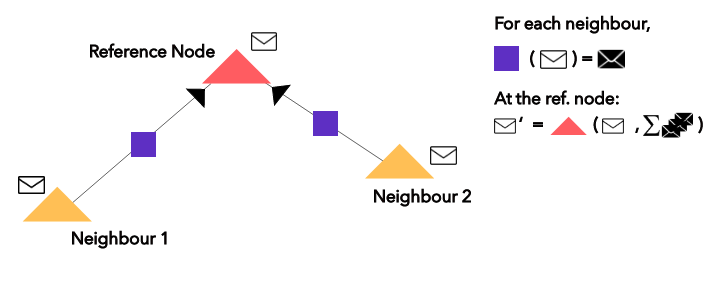
2. 接着为所有节点执行 n 次近邻聚合（也就是消息传递）；

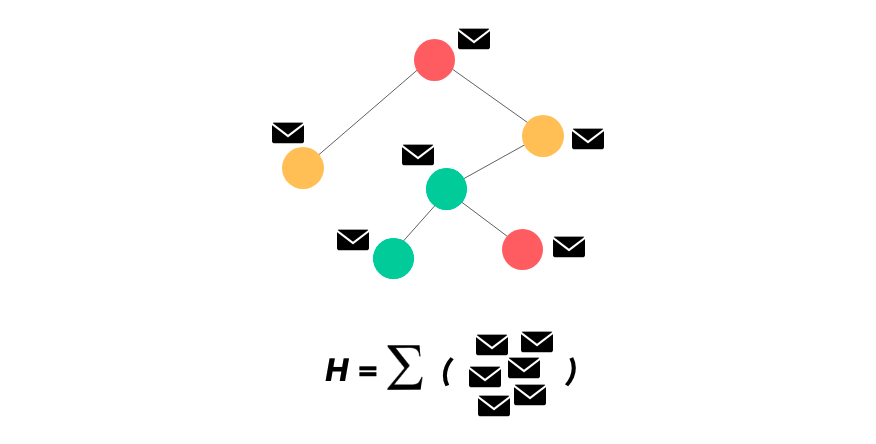
3. 然后再在所有节点的嵌入向量上求和以得到图表征 H；

4. 最后可以完全跳过 H 直接向更高层级进发或者也可使用 H 来表征该图的独有性质。

小结

现在我们清楚地了解图神经网络的运行方式了。得益于 GNN 在图节点之间依赖关系进行建模的强大性能，它在社交网络、知识图谱和推荐系统方面都有广泛的应用。以社交网络图为例，GNN 在内容推荐方面表现很好。举个例子，当一个用户关注另一个政治倾向相似的用户时，GNN 可用于节点分类，以预测是否可将网站上的特定内容发送到上述用户的新闻流；当 GNN 用于「推荐关注」时，系统可以考虑用户所在的行业，再提供潜在的连接——边分类。

图深度学习其实非常有趣。本文的亮点在于使用一些可视化图介绍了图神经网络的基础概念，但如果想要透彻地了解 GNN，大家最好自己写代码实现看看。

赠书《深入浅出图神经网络：GNN 原理解析》

想要更系统地学习图神经网络？机器之心联合极验团队向读者们赠送 20 本《深入浅出图神经网络：GNN 原理解析》。本书为极验 AI&图项目团队倾力之作！从原理、算法、实现、应用 4 个维度详细讲解图神经网络，理论与实践相结合。白翔、俞栋等学术界和企业界领军人物强烈推荐。

赠书方式：读者们可留言评论对图神经网络的理解，获得点赞量最高的 20 名读者可获得赠书 。

点击阅读原文，查看购买链接。