拥有悠久历史的聚合——《统计学七支柱》

“统计学是什么?”
统计学的七个基本思想——聚合、信息、似然、相互比较、回归、设计、残差
下文节选自《统计学七支柱》, 已获人邮图灵许可, [遇见数学] 特此表示感谢!
古代的聚合
1.2
统计概括与书写一样拥有悠久的历史。图1-6是一块大约公元前3000年(与书写的起源时间很接近)的苏美尔人的泥板文书复原品,由芝加哥大学东方研究所的同事克里斯·伍兹向我展示。
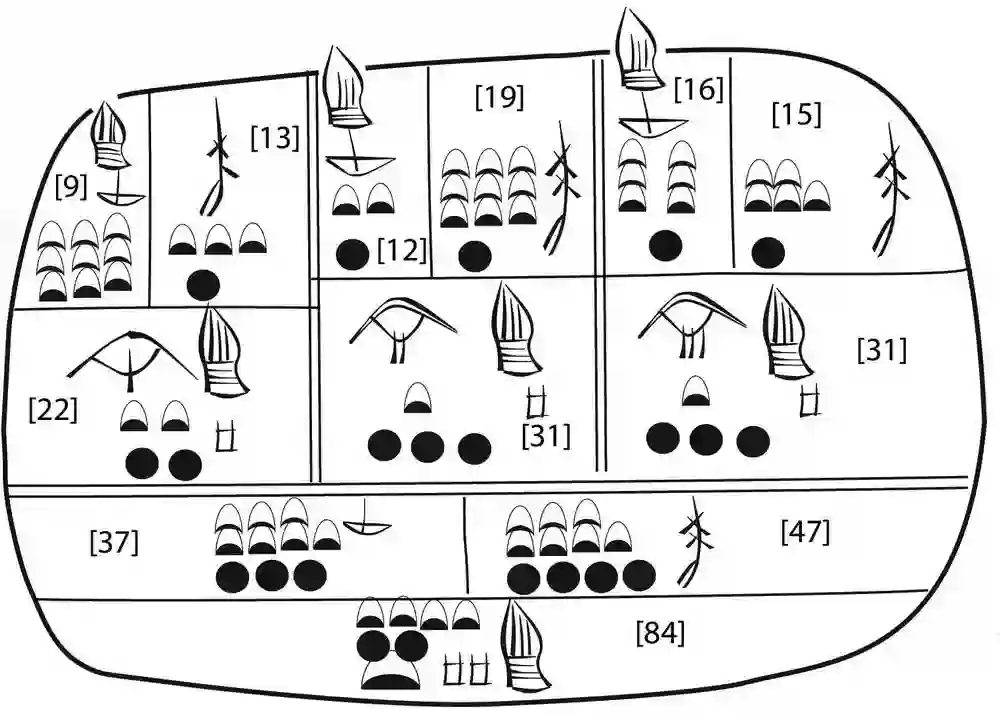
图1-6 一块大约公元前3000年的苏美尔人泥板文书重现,添加了现代的数字(由罗伯特·英格伦复原,参见Englund 1998, 第63页)
这块泥板代表的内容相当于一个2 × 3的列联表,显示了两种类型的商品计数,可能是两种作物3年内的产量(加上了现代的数字)。顶上一行显示了6个单元格,商品符号显示在相应的计数之上。第二行是年份或者列的总计,第三行是两种作物行的总计,底部是全体的合计值。今天我们会以不同方式重列这些数字,如表1-1所示。
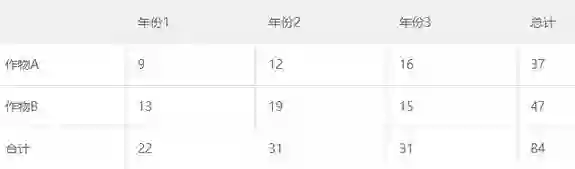
表1-1 苏美尔人泥板文书数字记录的列联表形式
统计分析没有保存下来,但可以确定其中不包括卡方检验。我们能说的是,这块泥板展现了那个时代的高水平统计智慧,但它没有离个别数据值走得太远:不仅表格主体展现了每年所有作物的计数,泥板背面还给出了这些计数依赖的原始数据、个体生产者的个数。甚至5000年前就有人认为公开原始数据是有用的!
数据统计的科学分析始于何时呢?算术平均值的使用是什么时候变为统计分析的一个正式组成部分的?真的没有在17世纪以前很久吗?为什么更早的时代没有用均值对天文、调查和经济进行组合观测?古代的均值数学是众所周知的。毕达哥拉斯学派在公元前280年已经了解均值的3种类型:算术平均值、几何平均值和调和平均值。公元1000年时,哲学家波伊修斯将均值数量提高到了至少10种,包括毕达哥拉斯的3种在内。不可否认,这些均值是在哲学意义下展开的,主要用于讨论线段的比例,以及音乐,而非用于数据总结。
我们当然可以期待,古希腊人、古罗马人或者古埃及人早在2000多年前日复一日的生活中,就已经摸索出对数据取均值。又或者他们并没有这样做,但可以肯定的是,早在1000年前的阿拉伯科学的杰出天文研究中,就可以找到均值。但是,哪怕只是想在这些来源中找到一个证据充分的例子,费尽心血广泛搜索之后,也总是免不了落空。
针对早期使用均值的历史,最坚定的搜索者是不屈不挠的研究者邱吉尔·艾森哈特,他在国家标准局度过了大部分职业生涯。数十年间,艾森哈特一直追踪均值的历史应用,并在1971年美国统计学会的主席演讲中总结了自己的研究。他热情洋溢地演讲了近2小时,但他发现的对于所有均值的相关使用工作、有证据表明使用均值的最早工作等,就是我前面提到过的由D. B. 和盖里布兰德做出的。艾森哈特发现,希帕克(大约公元前150年)以及托勒密(大约公元150年)对自己的统计方法默不作声,而阿尔-比鲁尼(大约公元1000年)则使用通过二分最小值和最大值之差产生的数——并不接近均值。均值很早就出现在印度的应用几何中,婆罗摩及多在公元628年写的一本关于测量的小册子中有这样的建议:处理挖掘问题时,要使用与挖掘平均规模相一致的长方体当作不规则挖掘量的近似值。
所有这些年代的历史证据表明,人们收集了许多类型的数据。某些情况下,不可避免需要概括。如果不使用平均值,人们需要做什么以进行总结呢?选定单个数字进行报告吗?我们先看几个例子,其中运用了类似于均值的概念,看完之后也许会更好地理解前统计时代人们是怎样看这些问题的。
修昔底德讲过一个关于攻城梯的故事,发生在公元前428年:
“一方为了达到敌人城墙的高度,需要制造一批梯子。因为城墙面向他们的一面粉刷不仔细,所以可以根据测量砖的层数计算城墙的高度。许多人同时数砖的层数,尽管有些人可能会数错,但大多数人会数对,尤其是多次计数之后。并且他们距离城墙也不远,完全可以看清楚。计算砖块的厚度后,就可以进一步推算梯子要求的长度了。”
修昔底德描述了所谓“众数”(mode,最频繁报告的值)的使用。因为计数过程缺失独立性的预期,众数并不非常精确。但如果报告非常接近,那它就和任何其他概括一样好。修昔底德并没有给出数据。
另一个很晚的例子来自16世纪早期,由雅各布·科贝尔在一本关于测量的图文并茂的书中提到。科贝尔说,那个时代土地测量的基本单位用一根16英尺长的木棒来确定。而且,当时的1英尺(foot)真的表示一只脚长,但是谁的脚呢?肯定不是国王的脚,也不是每次上台都会要求重新商定土地合约的新君主的脚。科贝尔说到的解决方案简单而优雅:在教堂礼拜之后留下16位市民代表(那时都是男性),他们鞋头对着鞋跟,站成一条线,这条线的长度就是那根16英尺木棒的长度。科贝尔的图片由他自己蚀刻,是一幅解释艺术的杰作(如图1-7所示)。

图1-7 科贝尔关于确定一根合法木棒的描述(Kobel 1522)
这真是一根“社区的”木棒!而且,这根木棒确定以后,又细分为16个相等的部分,每个部分都表示这根公共木棒中单只脚(即1英尺)的度量。从功能角度讲,这就是16个人的脚长的算术平均值,但“均值”这个术语在任何地方都未提及。
这两个例子相隔大约2000年,但它们都涉及一个共同问题:如何概括一组相似但不完全相同的测量。每种情况中,解决问题的方式反映了组合涉及的智力困难,这种困难到今天依然存在。在古代和中世纪,每当需要概括不同数据时,人们便选择个别的例子。修昔底德的故事中,被选中的个别例子是最主流的情形——众数。而在其他示例中,也可以选择那个最突出的例子;对数值数据而言,甚至可以选择最大的那个记录值。每个社会都希望宣扬它们最好的部分以代表整体社会,或者选择的情形也可以是基于不明确的理由而选择的“最佳”个体或值。天文学中,“最佳”值的选择可能反映了观测者的个人知识或观测的天文条件。但无论做了什么,这意味着要保持至少一个数据值的个别特征。科贝尔的记述中,重点是16只个体的脚,甚至可以在图片中认出那时的人们。无论如何,“由个体共同决定木棒长度”,这种思想是一个强有力的观点,因为这没有抛弃它们的个性。这是木棒合法性的关键,甚至也决定了单独的英尺标志是真正意义的平均。
非常感谢您的关注和支持!



