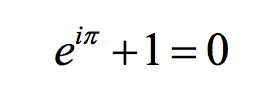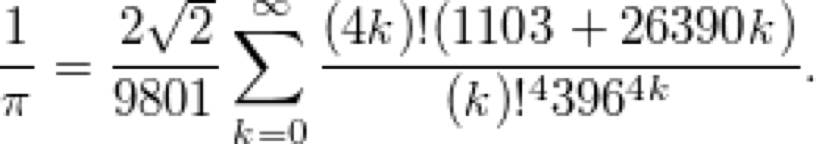为什么人类的大脑认为数学“美”？ | Front.Hum. Neurosci 论文推荐

2017 年 8 月 8 日 科研圈

作者 Josefina Alvarez

编译雷鸣

审校阿金

至真、至美的数学

“数学不仅至真，而且至美。”这是数学家、哲学家、诺贝尔文学奖获得者伯特兰·罗素（Bertrand Russell）在其《数学研究》里面的一段论述。在至真层面，数学作为物理世界的通用语言可以说当之无愧，它的功用和影响力几乎触及所有学科。但在美学层面，数学之美却是一个非常模糊的概念，相比“至真”的客观与精准，“至美”则掺杂更多主观因素，而且难以定性。不过可以肯定的是，无论数学之美到底如何，数学家已经从它的抽象能力及其在各领域建立的广泛联系发现数学所拥有的巨大审美价值。

图片来源：Image Jgmoxness, CC BY-SA 3.0.

上图展示的是248维对称体李群E8，此类可视化数学对象无疑是美的。然而数学本身是美的吗？数学之美与艺术之美到底有什么异同呢？不少人士把数学看作艺术，比如数学家 Armand Borel，他在《数学通讯》（The Mathematical Intelligencer）上发表文章表达了这种观点：“数学与艺术、实验科学、理论科学这三门学科拥有如此之多共性，所以理应同属于这三门学科，但同时也应与三者都有所不同。”

至于如何在数学与艺术之间建立合理的联系，答案是模糊不清的。数学之美，似乎是自然界有意给高冷的数学保留的一块世俗的领地。不过与此同时，或许有些不为人知的事情正在另外一些地方悄然发生。

大脑革命

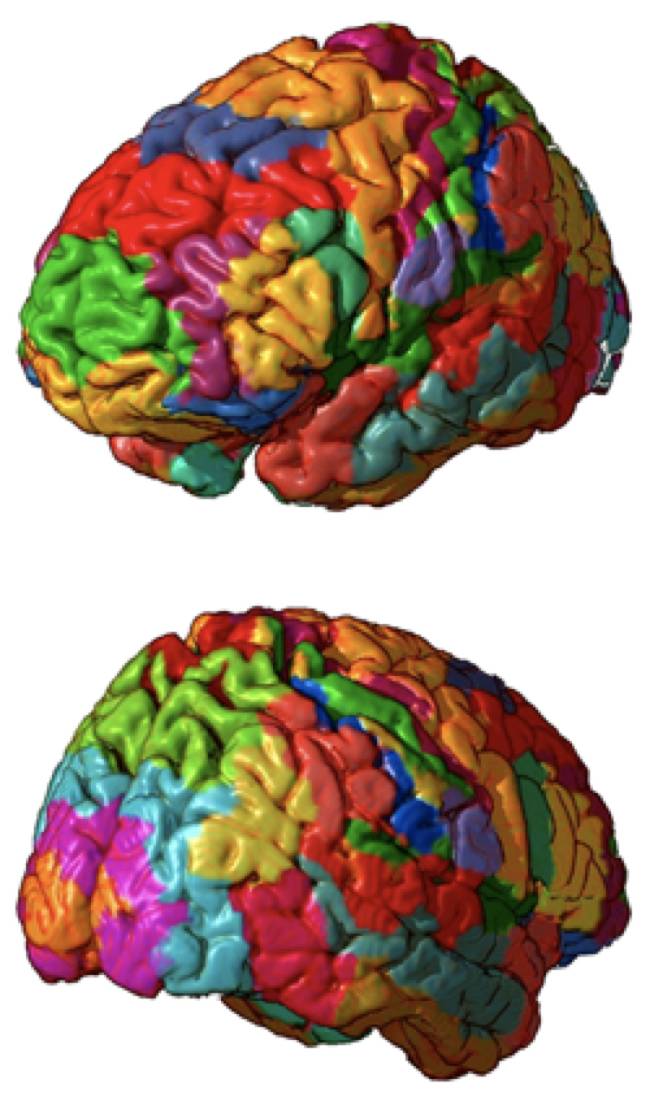
1909年，解剖学家科比尼安·布罗德曼（Korbinian Brodmann）根据细胞组织结构把大脑皮层划分为47个区域，现在称之为布罗德曼分区。后人发现，特定的细胞功能区与某些布罗德曼分区有着密切的关联。今天我们对细胞功能的广泛认识显示出大脑惊人的复杂性。例如，大约有三千多彼此连接的神经元控制我们的呼吸系统，相关神经元种类达65种之多。

在我们所谓的物理功能之外，研究人员正在深入研究大脑的智力功能。2011年一篇发表于 Neuro Image 期刊的文章发现了大脑的数字与计算功能区，同年 PLoS ONE 期刊为基于大脑的美学理论提供了论据。研究表明，视觉、听觉和道德体验感受到的美与所谓“大脑情感区”的活动有一定的关联。

图片来源：plus.maths.org

基于上述发现，神经生物学家 Semir Zeki 和 John Paul Romaya、物理学家 Dionigi M. T. Benincasa、数学家MichaelF. Atiyah，此四人专家组推测，感受数学之美所激发的大脑区域活动应与艺术之美的相同。2014年他们在Frontiers of human neuroscience期刊发表的一篇文章似乎验证了这一推测。在参与者面前呈现六十个数学公式，请他们把公式分成三个等级：丑陋、普通、美丽。结果欧拉方程被数学专业的参与者评选为最美的表达式，如下所示：

欧拉方程式把自然界最重要的五个常数，e、i 、pi、1，0 整合为一体，极简、极美。

与此同时，数学家斯里尼瓦瑟·拉马努金（SrinivasaRamanujan）以无穷级数表达的 1/pi，复杂得令人费解，被评为最丑的公式：

拉马努金的同事 Godfrey Hardy 说，这个公式必须是正确的，因为没有人能够杜撰如此复杂的东西。

数学专业人士做出上述选择，似乎是把朴素简单看作数学之美的重要属性。

“数学之美”与“数学之意”

虽然从神经生物学的角度来讲，数学之美与一般的美学具有相同特性，然而差别仍然存在。发现音乐之美，我们不需要理解其中复杂的乐理；同样，我们只需在本能层面感受绘画或者雕塑所呈现的美，而无需明白作品所运用的专业技巧。

然而，我们很难把“感受数学之美”与“理解数学之意”两种体验分别开来。前述研究的参与者有16位来自数学专业，另有12位来自非数学专业。在数学专业的参与者当中，“感受数学之美”与“理解数学之意”二者之间有很强的关联，但并非完全相关，有些公式即便他们已经充分理解，仍然被评为丑陋。同时，非数学专业的参与者也会把某些公式评为美丽，尽管他们并不能真正理解这些公式的奥妙。或许那些非数学专业的参与者喜欢那些公式所具有某些特质，比如对称性。因此，“感受数学之美”与“理解数学之意”二者之间到底有怎样的关联，仍然是未来需要我们深入研究的课题。

上述研究所运用的工具是一种磁共振成像设备（fMRI），美国化学家 Paul Lauterbur 和英国物理学家 Peter Mansfield 因为在 MRI 上面的贡献共同摘取2003年诺贝尔生物学奖章。总而言之，数学神奇的力量能够让我们更好地观察我们的精神世界，反过来也有助于我们理解数学的本质。

论文基本信息

题目

Theexperience of mathematical beauty and its neural correlates

作者

SemirZeki, John Paul Romaya, Dionigi M. T. Benincasa and Michael F. Atiyah

期刊 Front.Hum. Neurosci

日期 13February 2014

DOI 10.3389/fnhum.2014.00068

摘要

Manyhave written of the experience of mathematical beauty as being comparable tothat derived from the greatest art. This makes it interesting to learn whetherthe experience of beauty derived from such a highly intellectual and abstractsource as mathematics correlates with activity in the same part of theemotional brain as that derived from more sensory, perceptually based, sources.To determine this, we used functional magnetic resonance imaging (fMRI) toimage the activity in the brains of 15 mathematicians when they viewedmathematical formulae which they had individually rated as beautiful,indifferent or ugly. Results showed that the experience of mathematical beautycorrelates parametrically with activity in the same part of the emotional brain,namely field A1 of the medial orbito-frontal cortex (mOFC), as the experienceof beauty derived from other sources.

地址

http://journal.frontiersin.org/article/10.3389/fnhum.2014.00068/full

阅读更多

▽ 故事

· 颠覆认知！糖尿病可能像疯牛病一样传播？！

· “我不想拿一千块工资、住多人宿舍，还被海归碾压”

· 美国首次成功编辑人类胚胎，“定制人类”或将不再是科幻情节

· 清北生物博士给学弟学妹的万字建言：生物这行这么难，我们应该怎么办？

· 音乐的历史，即人类的历史 | Frontiers in Sociology 论文推荐

· 华人学者发现：恐龙灭绝时，蛙类大爆发 | PNAS 论文推荐

· Science：打破百年设计瓶颈光存储性能有望提高 40 倍 | 专访论文共同一作、南昌大学沈林放研究员

▽ 论文导读