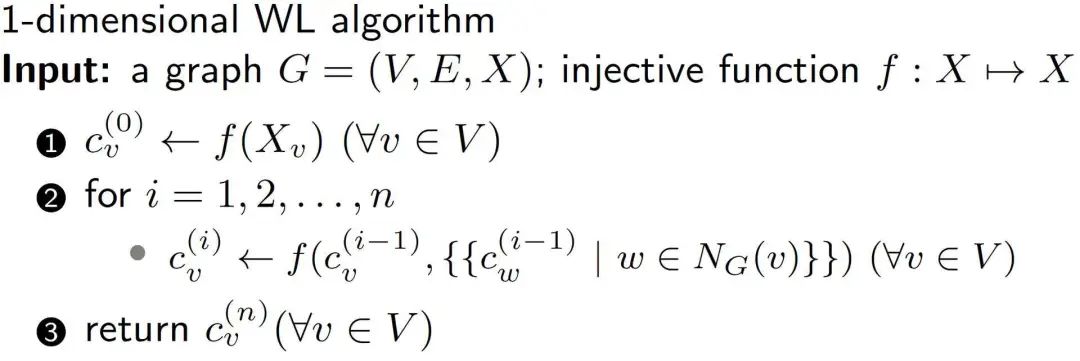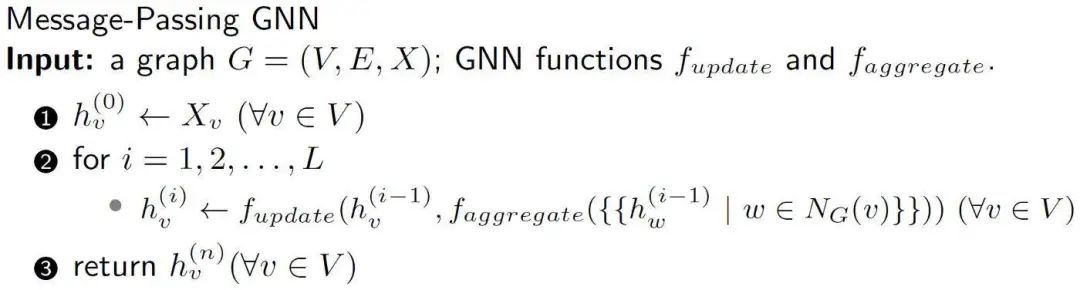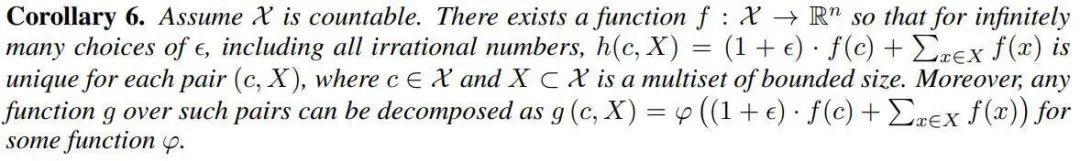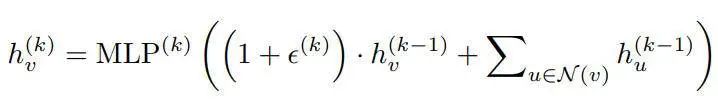浅谈图神经网络的局限性

作者 | Sergei Ivanov

译者 | Sambodhi

策划 | 赵钰莹

本文经原作者授权，由 InfoQ 中文站翻译并发布，未经许可禁止任何形式的转载。

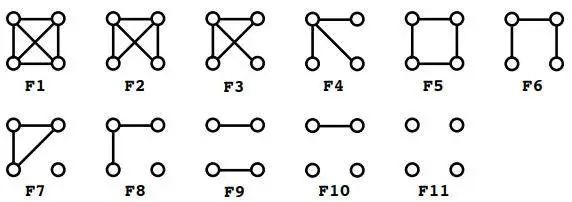
图表示有两种范式：图核（graph kernel）和图神经网络（graph neural network）。图核通常以无监督的方式基于分解创建图嵌入。例如，我们可以计算一个图中每种类型的三角形数量，或者更一般的三元组的数量，然后用这些计数来获得嵌入。这是众所周知的 Graphlet 核的实例。

所有大小为 4 的 Graphlet。计算一个图所有四元组中每个 Graphlet 的数量，将得到 Graphlet 核。来源：《用于大图比较的高效 Graphlet 核》（Efficient graphlet kernels for large graph comparison）

该范式的主要研究动机是，创建一种能够保持图之间同构的嵌入，即当且仅当两个图的对应嵌入相同时，两个图才是同构的。如果我们有这样的嵌入，就能解决图同构问题。这是目前已知的比 P 问题更难的问题。然而，还有一些嵌入，比如 Anonymous Walk Embeddings （匿名步行嵌入），它就保留了同构，当然，这是以运行时间计算为代价的。尽管如此，本文的主要信息是，图核是用来解决图同构问题的, 嵌入能区分的图越多，嵌入就越好。

译注：P 问题：如果一个问题可以找到能在多项式的时间里解决它的算法，那么这个问题就属于 P 问题。P 是英文单词多项式的第一个字母。具体请参见维基百科的词条 P/NP 问题。

随着图神经网络的出现，这一原则发生了改变。我们可以尝试解决任何给定的问题，例如寻找最短路径或检测循环，而不是解决一类问题，即图同构。这是很有前途的，因为它使我们用它能解决的问题来指导我们的网络设计。这听起来像是魔法：你只需训练你的网络，它就能为你找到解决方案，而不是使用一些成熟的组合算法。但它也有令人存疑之处：神经网络通过 SGD 算法搜索解决方案，并涉及到许多其他技术细节，如果你陷入了糟糕的局部最优，那该怎么办呢？它如何才能解决任何问题呢？事实上，图神经网络存在一些局限性。

图神经网络强大的条件

我将从《图神经网络有多强大》（ How Powerful are Graph Neural Networks）这篇论文开始，它引发了有关图神经网络理论解释的大量研究。特别是，将图神经网络与研究成熟的图同构算法——Weisfelier-Lehman（WL）算法进行了比较。

关于 WL 算法

这个算法很容易描述，可以从图开始。其中，每个节点都有对应的颜色（如果没有颜色的，就放置一个度数）。在每次迭代中，每个节点都会获得其邻居的一组颜色，并以特定方式更新其颜色。具体地说，存在一个单射函数（Injective function），根据节点的前一个颜色 C 和邻域的颜色 X 的有序列表，创建节点的新颜色 C’，该算法在 n 次迭代之后停止，并对图进行更新着色。

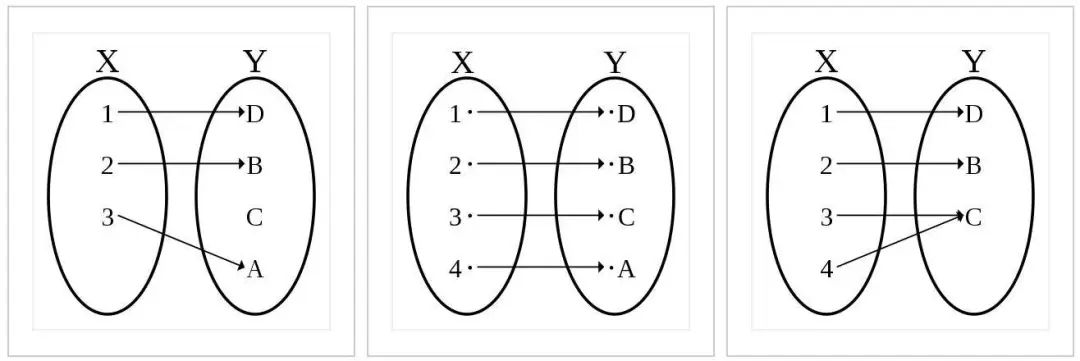
注意，WL 算法使用单射函数很重要，因为它保证了不同的输入将会得到不同的输出。WL 使用的一个特殊的单射函数 是为每个输入参数创建了之前未遇到过的新颜色。因为它在分类（可数）域（颜色）中运行，因此始终可以创建这样的映射。

从左到右依次为单射、双射、满射、映射（来源：https://en.wikipedia.org/）

该算法的主要用途是测试两个图之间的同构性。如果最终的着色不同，则说明两个图不是同构的。如果两个图具有相同的最终着色，那么 WL 算法输出它们可能是同构的，这意味着它们仍然不是同构的可能性非常小。

这个算法是 20 世纪 70 年代在苏联的秘密实验室设计的，当时计算机还在使用穿孔卡片。但从那时起，世界各地的研究者都在研究它的属性，特别是当 WL 算法失败时，我们由此知道了存在不同的图族。例如，对于任何具有 n 个顶点的 2- 正则图（regular graphs），最终的颜色将是相同的。尽管如此，这是对同构非常有力的检验，并且有定理指出，当 n 趋于无穷时，WL 失败的可能性变为 0。因此，这是一个相当强大的算法。

回到图神经网络

如果你研究过图神经网络，你会注意到图神经网络的更新节点特征的方式与 WL 算法更新节点颜色之间有许多相似之处。具体地说，图神经网络使用消息传递机制更新特征。

不同图神经网络之间的区别在于所使用的聚合函数和读出函数。但是很容易理解的是，如果聚合函数是单射的，那么如果 WL 将图映射到不同的颜色，则图神经网络也会将这些图映射到不同的嵌入。定理 3 是表达这种说法的一种正式方式。

也就是说，图神经网络有参数化函数 φ和 f，如果它们是单射的，则可以保证图神经网络的强幂。这并不奇怪，因为 WL 算法也要求它的函数是单射的，而且在其他方面，这两个过程是等价的。

注意，这里有一种更新节点嵌入的特殊方式。我们得到先前嵌入 h_v^(k-1)，以及邻居先前嵌入的多重集，这是两个不同的参数，这一点很重要。

因此，你可以使用图神经网络来确定图是否同构，这将等同于使用 WL 算法。

图神经网络突然变成众所周知的算法，它的局限性又在哪里呢？

关于图神经网络的局限性

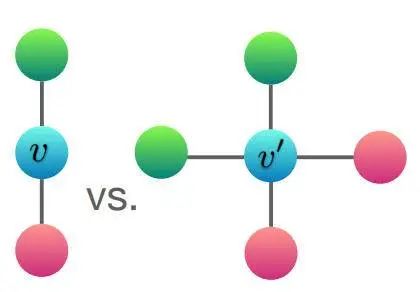
前文提到的主要限制是，需要有单射函数 φ 和 f 。这些是将嵌入的多重集映射到新嵌入的函数。例如，你可以使用均值函数。这个函数将获取嵌入的平均值，并将其分配为新的嵌入。但是，很容易看出，对于某些不同的图，它们会给出相同的嵌入，所以，均值函数并不是单射的。

即使图不同，节点 v 和 v’ 的平均嵌入聚合（此处嵌入对应于不同的颜色）将给出相同的嵌入。来源：《图神经网络有多强大》（How Powerful are Graph Neural Networks）

但是，如果你以一种特定的方式进行求和并变换嵌入，那么就有可能得到单射。这是引理 5：

这里真正重要的是，你可以先用某个函数 f(x) 将每个嵌入映射到一个新的嵌入，然后进行求和，得到一个单射函数。在证明中，它们实际上显式地声明了这个函数 f，这需要两个额外条件，即 X 是可数的，且任何多重集都是有界的。我认为这两个假设都不强，因为无论如何，我们将图神经网络应用于有限图，其中，特征和邻域的基数都是有限的。但至少我们现在知道，如果我们使用变换 f，然后进行加法运算，我们就可以得到一个单射映射。

但是，根据上面的定理 3（条件 a），应该存在一个特定的聚合方案，该方案除了对邻居进行聚合外，还对当前节点 h_v^(k-1) 使用先前的嵌入。要包含它，我们需要另一个声明：

注意，这里的函数 h 如前所述，取变换后的邻居特征之和，但除此之外，加上 (1+eps)f(c)，这个 eps 是任意无理数。这样函数 h 是单射的。

到这一步，我们知道聚合函数 φ 和 f 应该是单射的，而且，我们有一个函数 h 是单射的。如果目标是构建强大的嵌入，那么已经完成了目标。但是，我们要尝试的不只是构建嵌入，还要尝试以有监督的方式来解决下游任务，如节点分类。并且函数 h 并没有可学习的参数来对数据进行拟合（也许 eps 除外）。

GIN 架构提出的替代方案是用 MLP 替换函数 φ 和 f，并且由于通用近似定理（universal approximation theorem），我们知道，MLP 可以近似任何函数，包括单射函数。因此，具体地说，GIN 的嵌入更新具有以下形式：

注意，MLP 内部的东西并不能保证是单射的，而且 MLP 本身也不能保证是单射的。事实上，对于第一层，如果输入特征是独热编码（one-hot encode），那么 MLP 内部的和将是单射的，原则上，MLP 可以学习单射函数。但是在第二层及后面的层，节点嵌入变得不合理，很容易举出一个例子，其中嵌入的和将不再是单射的（例如，有一个嵌入等于 2 的邻居，或有两个嵌入等于 1 的邻居）。

因此，当 MLP 和嵌入和都是单射函数时，GIN 算法的性能与 WL 算法相当。

但事实上，在训练中并没有任何东西可以保证这种单射性，而且可能还会有一些图是 GIN 无法区分的，但 WL 可以。所以这是对 GIN 的一个很强的假设，如果违反了这一假设，那么 GIN 的性能将受到限制。

这种局限性，后来在《判别结构图分类》（ Discriminative structural graph classification）论文中进行了讨论，论文表明，为了使 MLP 单射，输出嵌入的大小应与输入特征的大小成指数关系，尽管分析是无界邻域进行的（即无限图）。找到具有单射聚合并且能够充分表达下游任务的架构是一个有待解决的问题，尽管有几种架构将 GIN 推广到更高维的 WL 算法以及其他问题；然而，还不能保证所学到的图神经网络架构能够解决所有输入图的特定任务。论文《图神经网络表达能力研究综述》（ A Survey on The Expressive Power of Graph Neural Networks ），很好地解释了近年来在图神经网络表达能力的理论解释方面取得的进展。

结语

图神经网络属性的研究现在是一个活跃的研究领域（你可以查看最近的趋势），有许多悬而未决的问题需要解决。本文的主要目的是向读者说明，目前，图神经网络并不能保证能够收敛到像 WL 算法一样强大的状态，尽管一般情况下，当图神经网络变得同样强大时，通常会有一组参数。图神经网络可以解决图形上的不同问题，但到目前为止，研究的重点主要集中在它们能够解决或不能解决的问题上，这将是下一篇研究论文的重点。

作者介绍：

Sergei Ivanov，机器学习研究科学家，专注于图机器学习和建议。

扩展链接：

https://towardsdatascience.com/limitations-of-graph-neural-networks-2412fffe677

点个在看少个 bug 👇