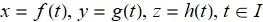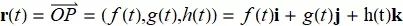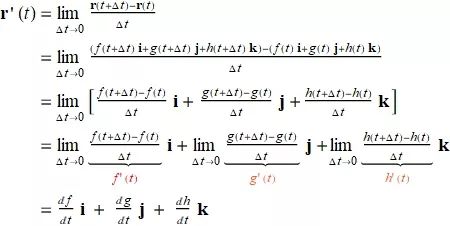【向量值函数和空间曲线】图解高等数学-下 06
10.5 向量值函数和空间曲线
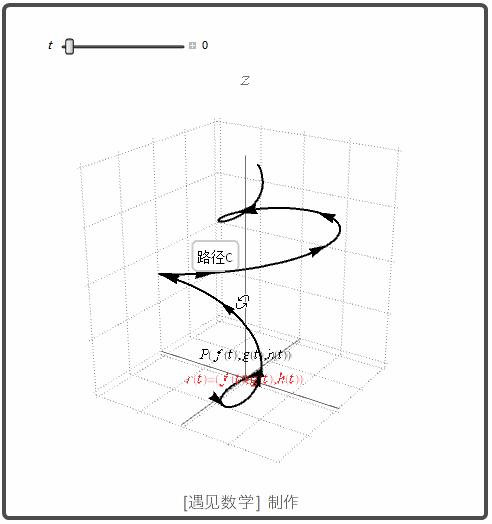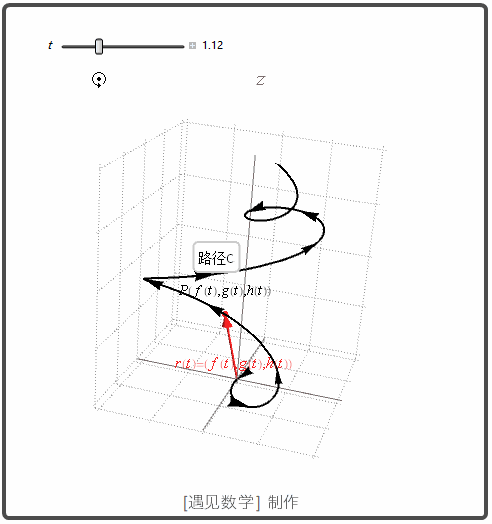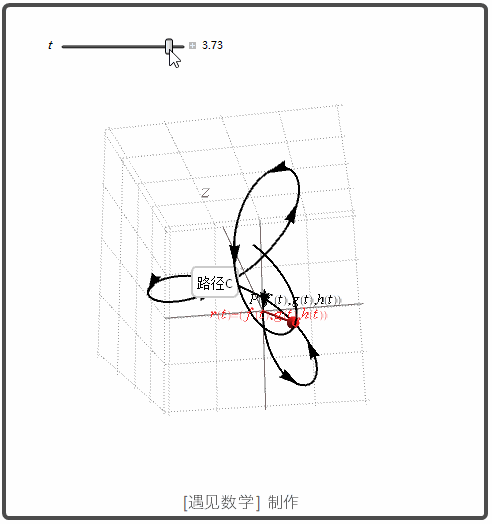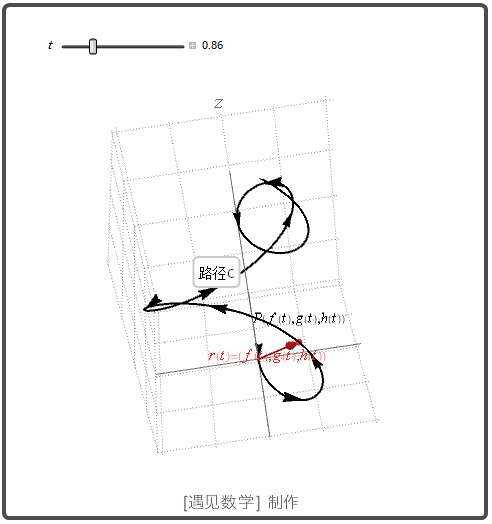
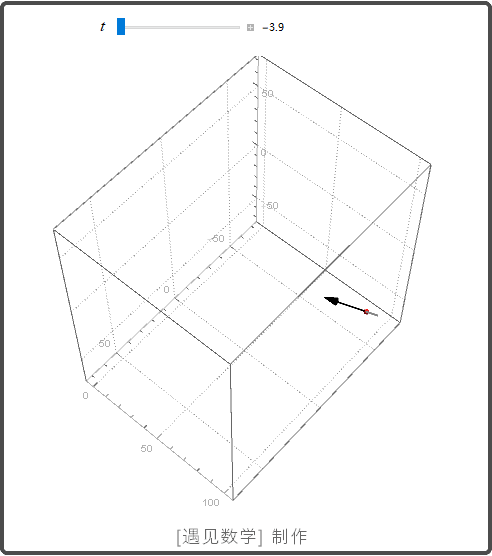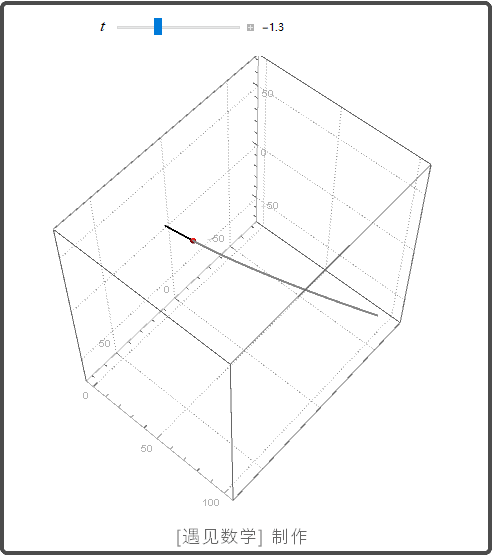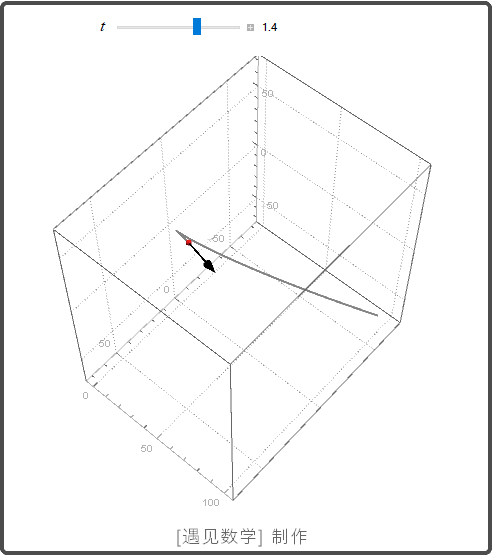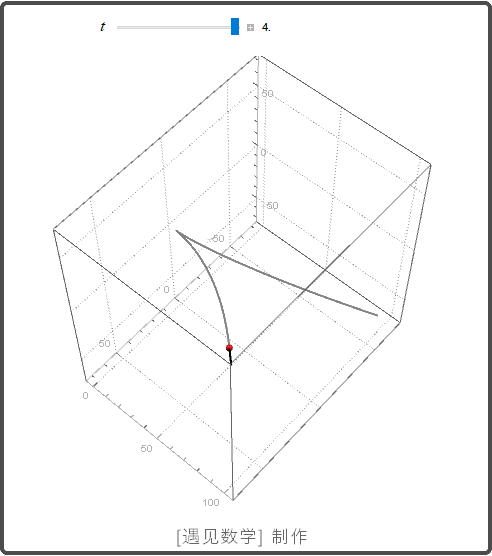
空间曲线
极限和连续
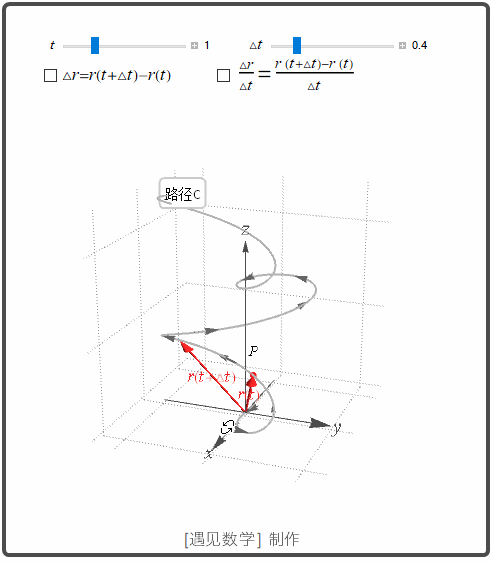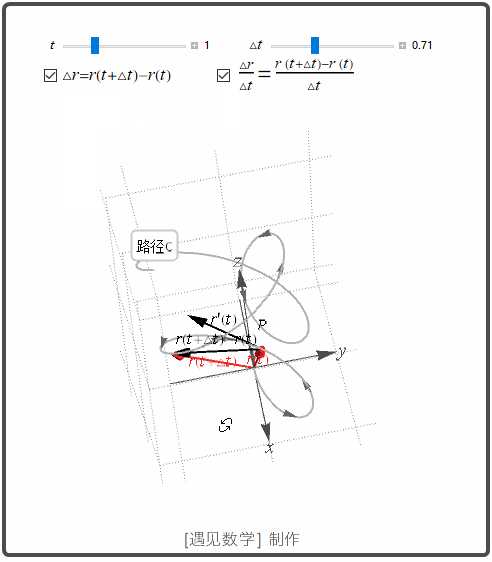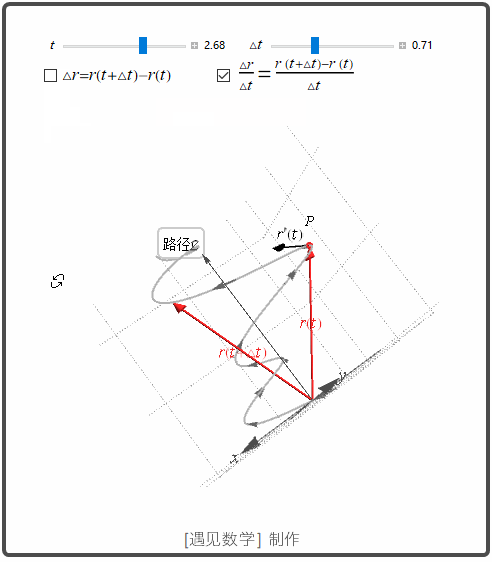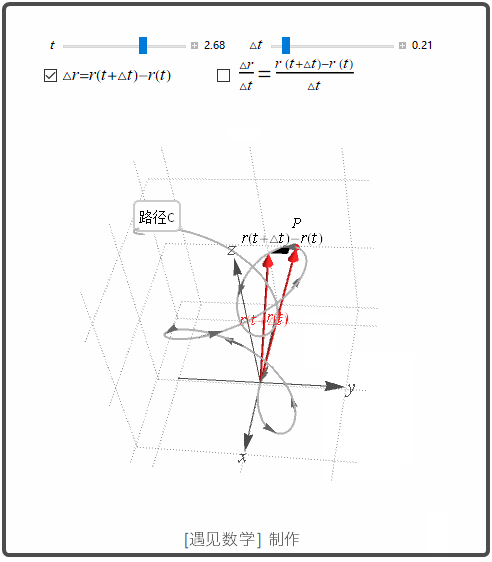
导数和运动
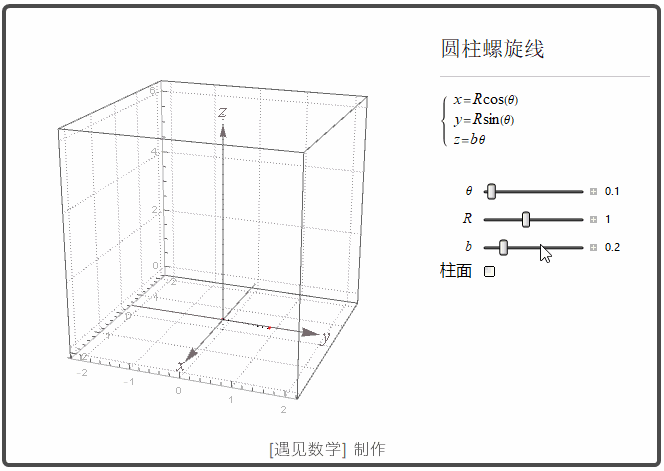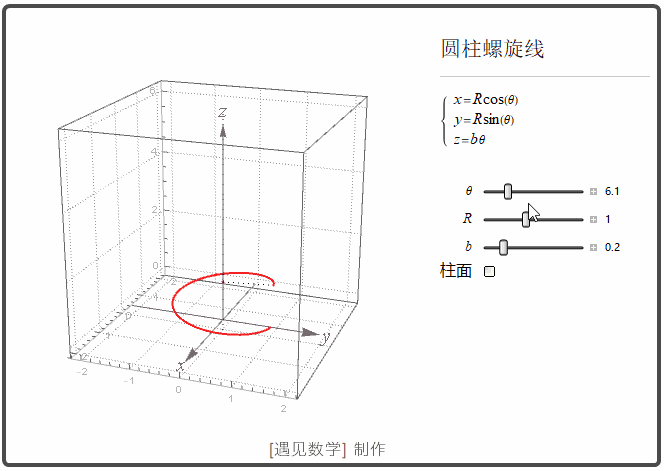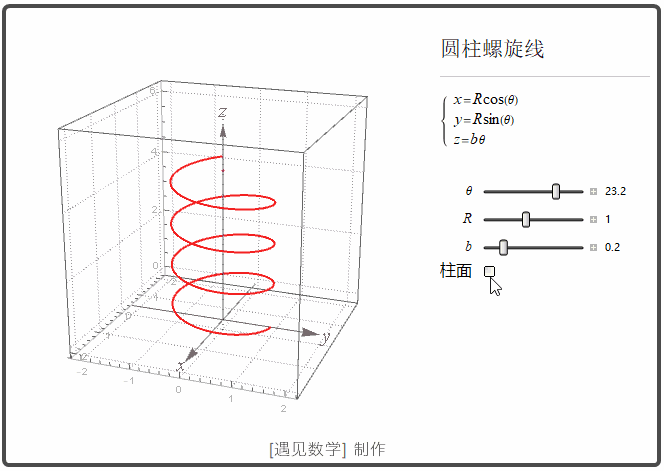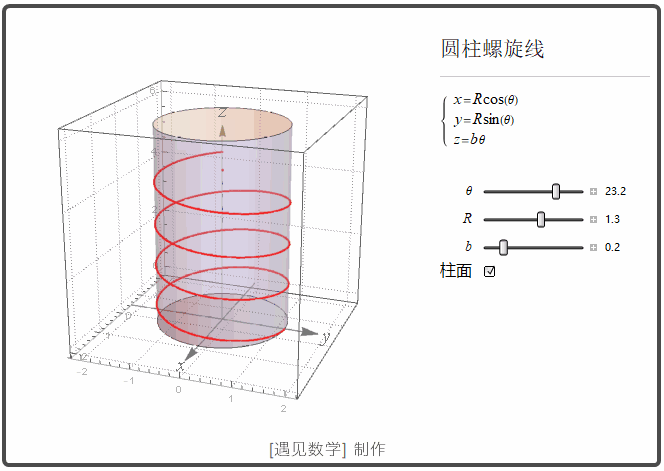
圆柱螺线
速度, 加速度, 运动方向
微分法则
登录查看更多
相关内容
专知会员服务
54+阅读 · 2020年3月5日
专知会员服务
16+阅读 · 2019年11月30日
Arxiv
3+阅读 · 2018年4月20日
Arxiv
8+阅读 · 2018年3月29日
Arxiv
10+阅读 · 2018年2月27日
Arxiv
15+阅读 · 2018年1月5日