卷积神经网络（CNN）详解及资料整理

2018 年 9 月 17 日 AI研习社

本文为 AI 研习社编译的技术博客，原标题Convolutional Neural Network (CNN)。

翻译 | 老赵校对 | 江舟整理 | 志豪

原文链接：

https://skymind.ai/wiki/convolutional-network#intro

内容

深度神经网络介绍

图像是4维张量吗？

卷积神经网络定义

深度神经网络如何工作？

池化/下采样

展示代码

更多卷积神经网络资料

深度神经网络介绍

卷积神经网络是深度人工神经网络，主要用于图像分类（比如，对你看到的进行命名），通过相似度聚类（图像搜索），并在场景中执行对象识别。它们是可以识别面部，个体，街道标志，肿瘤，鸭嘴兽和视觉数据的许多其他方面的算法。

卷积网络使用光学字符识别（OCR）进行数字化文本，并使模拟和手写文档上的自然语言处理成为可能，其中图像是要转录的符号。当声音被可视化为频谱图时，CNN也可以应用于声音。最近，卷积网络已经直接应用于文本分析以及具有图像卷积网络的图像数据。

卷积网络（ConvNets或CNN）在图像识别中的效果是世界广泛使用深度学习功能的主要原因之一。它们推动了计算机视觉（CV）的重大进步，它在自动驾驶汽车，机器人，无人机，安全，医疗诊断以及视障人士的治疗方面具有明显的应用。

图像是4维张量吗？

卷积神经网络使用张量输入和处理图像，张量是具有附加维度的数字矩阵。

它们很难被可视化，所以让我们通过类比来理解它们。标量只是一个数字，例如7; 向量是一个数字列表（例如，[7,8,9]）；矩阵是一个矩形的数字网格，占用多个行和列，就像电子表格一样。几何上，如果标量是零维的点，则矢量是一维的线，矩阵是二维平面，一堆矩阵排列在一起则是三维立方体，当这些矩阵的每个元素都有一堆映射到它的特征时，你就得到了第四个维度。作为参考，这是一个2 x 2矩阵：

[ 1, 2 ] [ 5, 8 ]

张量包含超出该二维平面的尺寸。你可以将数字排列在一个立方体中，就会轻松地画出一个三维张量。这是一个以平坦方式呈现的2 x 3 x 2张量（它画出了每个沿z轴延伸的2元数组的底部元素，直观地理解为什么它被称为三维数组）：

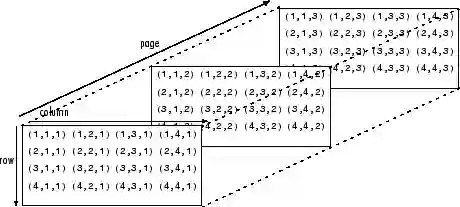
在代码中，上面的张量会被写成这样：[ [ [2,3], [3,5], [4,7] ], [ [3,4], [4,6], [5,8] ] ]。可视化为：

换句话说，张量是由嵌套在数组中的数组形成的，并且可以进行无限嵌套，任意数量的维数远远大于我们在空间上可以看到的维数。四维张量可以用嵌套一层更深的数组来简单替换这些标量中的每一个。卷积网络处理4维张量，如下所示（注意嵌套数组）。

ND4J 和 Deeplearning4j 使用：

NDArray

它与张量或多维数组具有相同意思。张量的维数：

（1,2,3...n）

称为张量的阶数；即五阶张量将具有五个维度。

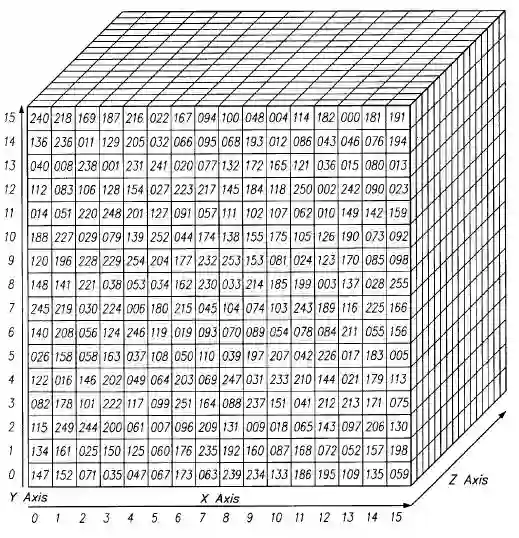
图像的宽度和高度很容易理解。由于颜色的编码方式，深度是必要的。例如，红绿蓝（RGB）编码产生三层深的图像。每一层都被称为“通道”，通过卷积，它产生一堆特征映射（下面将解释），它存在于第四维，就在时间本身的维度上。（特征只是图像的细节，如直线或曲线，卷积网络为其创建映射）。

因此，在卷积网中，图像不被视为二维区域，而被视为四维物体。下面将更全面地探讨这些想法。

卷积定义

从拉丁语convolvere来看，“to convolve”意味着一起滚动。出于数学目的，卷积是测量两个函数重叠程度的积分。将卷积视为通过将两个函数相乘来混合两个函数的方法。

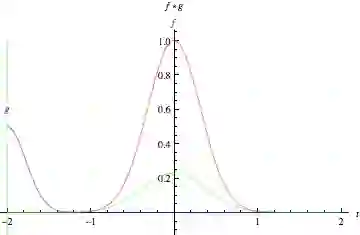
图片来源：Mathworld。 “绿色曲线是作为 t 的函数，表示蓝色和红色曲线的卷积，垂直绿线对应相应的x值。灰色区域表示 g(tau)f(t-tau) 的积，它是 t 的函数，因此其作为t的函数的面积恰好是卷积。

看看站在图表中间的高而窄的钟形曲线。积分是该曲线下的面积。靠近它的是第二条钟形曲线，它更短更宽，从图的左侧慢慢向右漂移。这两个函数在沿x轴的每个点处重叠的乘积是它们的卷积。所以从某种意义上说，这两个函数正在“融合在一起”。

通过图像分析，静态的基础函数（相当于静止的钟形曲线）是被分析的输入图像，第二个移动函数被称为滤波器，因为它拾取图像中的信号或特征。这两个函数通过乘法相关联。要将卷积可视化为矩阵而不是钟形曲线，请参阅Andrej Karpathy在“Convolution Demo”中出色的动画。

关于卷积网络的下一个要点是它们在单个图像上通过了许多滤波器，每个滤波器都会拾取不同的信号。在相当早期的一层，你可以将它们想象为通过水平线滤波器，垂直线滤波器和对角线滤波器来创建图像中关于边缘的图。

卷积网络采用这些滤波器，图像特征空间的切片，并逐个映射它们; 也就是说，他们会创建一张地图，显示每个特征出现的地方。通过学习特征空间的不同部分，卷积网络允许轻松扩展和健壮的特征工程特性。

（请注意，卷积网以不同于RBMs的方式分析图像。虽然RBMs学习重建和识别每个图像的整体特征，但卷积网学习我们称之为特征图的图像片段）

因此卷积网络执行某种搜索。想象一下，一个小放大镜从左向右滑过一个较大的图像，一旦到达一个通道的末尾就会在左边重新开始（就像打字机一样）。那个移动的窗口只能识别一件东西，比如一条短的垂直线。三个暗像素堆叠在一起。它在图像的实际像素上移动垂直线识别过滤器，寻找匹配。

每次找到匹配时，它都会被映射到该视觉元素特有的特征空间上。在那个空间中，每个垂直线匹配的位置都会被记录下来，有点像观鸟者在地图上留下大头针来标记他们最后一次看到一只巨大的蓝鹭的位置。卷积网络在单个图像上运行许多次搜索 ——水平线，对角线，与要搜索的视觉元素一样多。

卷积网络对输入执行的操作比卷积本身要多。

在卷积层之后，输入通过非线性变换（例如tanh或relu函数），将输入值压缩到介于-1和1之间的范围内。

卷积神经网络是如何工作的？

关于卷积网络，首先要知道的是，它们不像人类那样感知图像。因此，你必须以不同的方式思考图像被馈送到卷积网络并由卷积网络处理时的含义。

卷积网络将图像视为很多层卷; 比如三维物体，而不是仅通过宽度和高度来测量的平面画布。这是因为数字彩色图像具有红 - 蓝 - 绿（RGB）编码，混合这三种颜色以产生人类感知的色谱。卷积网络将这些图像输入为三个独立的颜色通道，一个层叠在另一个之上。

因此，卷积网络接收一个普通彩色图像，就像一个矩形盒子，其宽度和高度由沿着这些维度的像素数量来测量，深度为三层，RGB中每个字母对应一层。这些深度层被称为通道。

当图像通过卷积网络时，我们将根据输入卷和输出卷来描述它们，在数学上将它们表示为这种形式的多维矩阵：30x30x3。从一层到另一层，它们的尺寸会发生变化，原因将在下面解释。

你需要密切关注图像卷层每个维度的精确度量，因为它们是用于处理图像的线性代数运算的基础。

现在，对于图像的每个像素，R，G和B的强度将由数字表示，该数字将是三个堆叠二维矩阵中的一个矩阵中的一个元素，这三个矩阵一起形成图像卷层。

这些数字是输入卷积网络的初始、原始、感官特征，ConvNets的目的是找出这些数字中的哪一个是有助于更准确分类图像的重要信号。（就像我们讨论过的其他前馈网络一样）。

卷积网不是一次只关注一个像素，而是采用方形的像素块并将它们传递给滤波器。该滤波器也是比图像本身小的正方形矩阵，大小与patch 相同。它也被称为内核，对于那些熟悉支持向量机的人来说，这将敲响警钟，过滤器的工作是在像素中找到模式。

这部优秀动画的功劳归于Andrej Karpathy。

想象两个矩阵。一个是30x30，另一个是3x3。也就是说，滤波器覆盖一个图像通道表面区域的百分之一。

我们将使用此图像通道像素块和滤波器的点积。如果两个矩阵在相同位置具有高的灰度值，则输出的点积值也是高的。否则，输出就会产生很低的点积。通过这种方式，单个值（输出的点积）可以告诉我们底层图像中的像素图案是否与滤波器表示的像素图案匹配。

让我们假设滤波器表示一条水平线，第二行有高值，第一和第三行有低值。现在想象我们从底层图像的左上角开始，然后我们一步一步地将滤波器移过图像，直到它到达右上角。步长的大小称为步幅。你可以一次将滤波器移动一列，也可以选择更大的步幅。

在每个步骤中，你取另一个点积，并将该点积的结果放在第三个被称为激活图矩阵中。激活图的宽度或列数等于滤波器遍历底层图像所用的步数。由于更大的步幅导致更少的步骤，因此大步幅将产生更小的激活图。这一点很重要，因为卷积网络在每一层处理和产生的矩阵的大小与它们的计算成本以及它们需要多长时间训练成正比。更大的步幅意味着更少的时间和计算量。

滤波器最先叠加在前三行上并滑过它们，然后再次从同一图像的第4 - 6行开始。如果它步幅为3，那么它将产生一个10x10的点积矩阵。表示水平线的相同滤波器可以应用于底层图像R，G和B的所有三个通道。并且可以将三个10x10激活图添加到一起，以便在所有三个通道上的水平线的聚合激活图也是10x10。

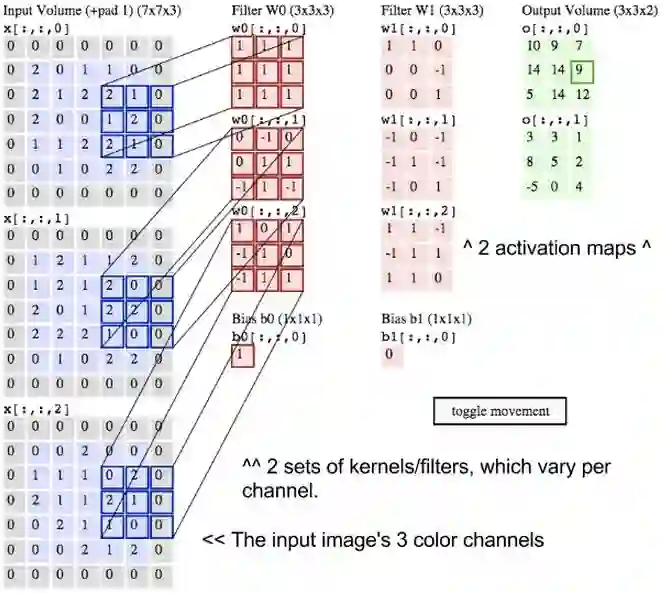
现在，因为图像在许多方向上都有线条，并且包含许多不同类型的形状和像素模式，所以你需要在底层图像上滑动其他滤波器以搜索这些模式。例如，你可以在像素中查找96种不同的模式。这96个模式将创建96个激活映射形成的堆栈，从而产生一个10x10x96的新卷。在下图中，我们重新标记了输入图像，内核和输出激活图。

我们刚刚描述的是卷积。你可以将卷积视为信号处理中使用的一种奇特的乘法。考虑创建两个矩阵的点积的另一种方法是当做两个函数。图像是底层函数，滤波器是你在底层函数上滚动的函数。

图像的主要问题之一是它们是高维的，这意味着它们需要花费大量的时间和计算能力来处理。卷积网络旨在以各种方式降低图像的维度。滤波器步幅是降低维度的一种方法。另一种方式是通过下采样。

CNNs进行最大池化/下采样

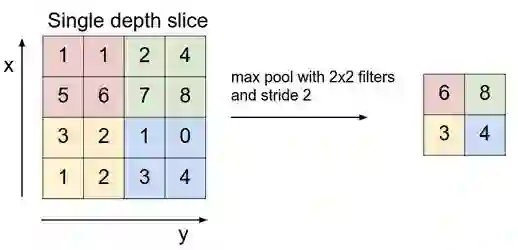
卷积网络中的下一层有三个名称：最大池化，下采样和子采样。激活图被馈送到下采样层，并且像卷积一样，该方法一次应用一个像素块。在这种情况下，最大池化只从图像的一个像素块中获取最大值，将其放置在与其他像素块的最大值相邻的新矩阵中，并丢弃激活映射中包含的其余信息。

图片来源 Andrej Karpathy.

只有图像上显示与每个特征相关性最强的位置(最大值)被保留下来，这些最大值组合在一起形成了一个低维空间。

在这一步中，许多关于较小价值的信息丢失了，这刺激了对替代方法的研究。但是，下采样具有优势，正是因为信息丢失，减少了所需的存储量和处理量。

交替层

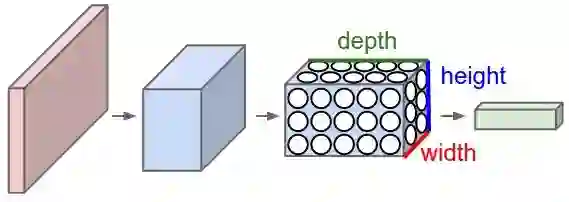
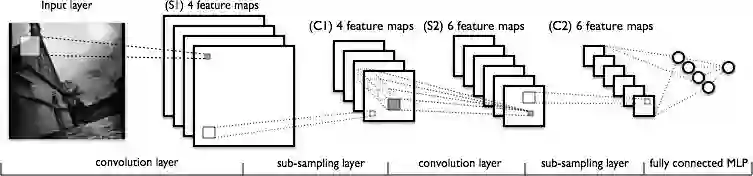
下图是展示典型卷积网络中涉及的变换序列的另一次尝试。

从左到右，你会看到：

1. 扫描实际输入图像得到特征。浅色矩形是经过它的滤波器。

2. 激活图堆叠在一起，每个激活图使用一个过滤器。较大的矩形是一个要下采样的块。

3. 通过下采样压缩的激活图。

4. 通过在第一个下采样堆上传递滤波器创建的一组新的激活映射图。

5. 第二次下采样，压缩第二组激活映射图。

6. 一个全连接层，对每个节点带有一个标签的输出进行分类。

随着越来越多的信息丢失，卷积网络处理的模式变得更加抽象，并且变得离我们人类识别的视觉模式越来越远。所以如果卷积网络在他们变得更深入时不能提供简单的直觉感受，请原谅你自己和我们。

D4LJ代码示例

以下是如何使用Deeplearning4j配置ConvNet的一个示例：

Create an iterator using the batch size for one iteration
     */
    log.info("Load data....");
    DataSetIterator mnistTrain = new MnistDataSetIterator(batchSize,true,12345);
    DataSetIterator mnistTest = new MnistDataSetIterator(batchSize,false,12345);
    /*
        Construct the neural network
     */
    log.info("Build model....");
    // learning rate schedule in the form of <Iteration #, Learning Rate>
    Map<Integer, Double> lrSchedule = new HashMap<>();
    lrSchedule.put(0, 0.01);
    lrSchedule.put(1000, 0.005);
    lrSchedule.put(3000, 0.001);
    MultiLayerConfiguration conf = new NeuralNetConfiguration.Builder()
            .seed(seed)
            .l2(0.0005)
            .weightInit(WeightInit.XAVIER)
            .updater(new Nesterovs(0.01, 0.9))
            .list()
            .layer(0, new ConvolutionLayer.Builder(5, 5)
                    //nIn and nOut specify depth. nIn here is the nChannels and nOut is the number of filters to be applied
                    .nIn(nChannels)
                    .stride(1, 1)
                    .nOut(20)
                    .activation(Activation.IDENTITY)
                    .build())
            .layer(1, new SubsamplingLayer.Builder(PoolingType.MAX)
                    .kernelSize(2,2)
                    .stride(2,2)
                    .build())
            .layer(2, new ConvolutionLayer.Builder(5, 5)
                    //Note that nIn need not be specified in later layers
                    .stride(1, 1)
                    .nOut(50)
                    .activation(Activation.IDENTITY)
                    .build())
            .layer(3, new SubsamplingLayer.Builder(PoolingType.MAX)
                    .kernelSize(2,2)
                    .stride(2,2)
                    .build())
            .layer(4, new DenseLayer.Builder().activation(Activation.RELU)
                    .nOut(500).build())
            .layer(5, new OutputLayer.Builder(LossFunctions.LossFunction.NEGATIVELOGLIKELIHOOD)
                    .nOut(outputNum)
                    .activation(Activation.SOFTMAX)
                    .build())
            .setInputType(InputType.convolutionalFlat(28,28,1)) //See note below
            .backprop(true).pretrain(false).build();
    /*
    Regarding the .setInputType(InputType.convolutionalFlat(28,28,1)) line: This does a few things.
    (a) It adds preprocessors, which handle things like the transition between the convolutional/subsampling layers
        and the dense layer
    (b) Does some additional configuration validation
    (c) Where necessary, sets the nIn (number of input neurons, or input depth in the case of CNNs) values for each
        layer based on the size of the previous layer (but it won't override values manually set by the user)
    InputTypes can be used with other layer types too (RNNs, MLPs etc) not just CNNs.
    For normal images (when using ImageRecordReader) use InputType.convolutional(height,width,depth).
    MNIST record reader is a special case, that outputs 28x28 pixel grayscale (nChannels=1) images, in a "flattened"
    row vector format (i.e., 1x784 vectors), hence the "convolutionalFlat" input type used here.
    */
    MultiLayerNetwork model = new MultiLayerNetwork(conf);
    model.init();
    log.info("Train model....");
    model.setListeners(new ScoreIterationListener(10)); //Print score every 10 iterations
    for( int i=0; i<nEpochs; i++ ) {
        model.fit(mnistTrain);
        log.info("*** Completed epoch {} ***", i);
        log.info("Evaluate model....");
        Evaluation eval = model.evaluate(mnistTest);
        log.info(eval.stats());
        mnistTest.reset();
    }
    log.info("****************Example finished********************");
}