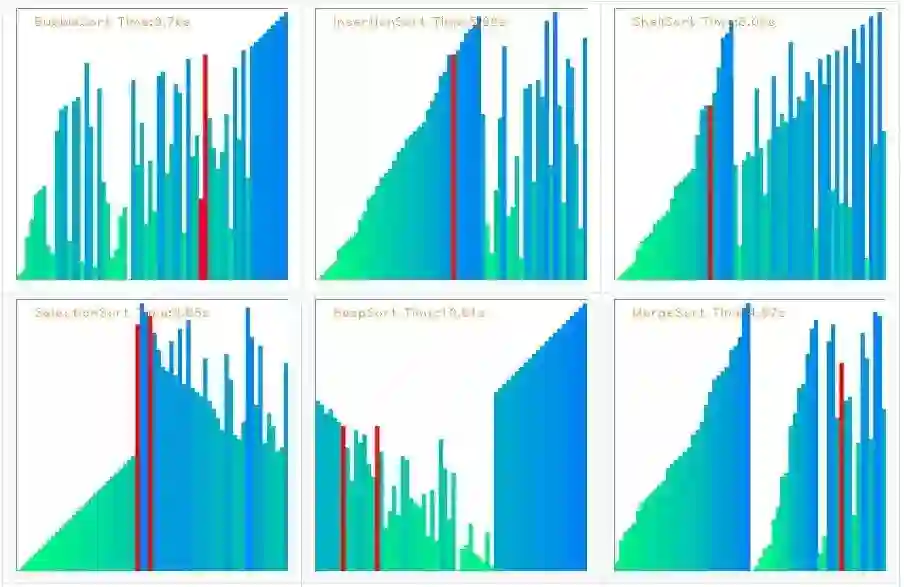
3分钟快速实现：9种经典排序算法的可视化

会员服务 ·

3分钟快速实现：9种经典排序算法的可视化

2019 年 5 月 15 日 AI100

作者 | 爱笑的眼睛

来源 | 恋习Python（ID:sldata2017）

最近在某网站上看到一个视频，是关于排序算法的可视化的，看着挺有意思的，也特别喜感。

▼

6分钟演示15种排序算法

不知道作者是怎么做的，但是突然很想自己实现一遍，而且用python实现特别快，花了一天的时间，完成了这个项目。主要包括希尔排序（Shell Sort）、选择排序（Selection Sort）、快速排序（Quick Sort）、归并排序（Merge Sort）等九种排序。

附上源码链接：

https://github.com/ZQPei/Sorting_Visualization

（觉得不错，记得帮忙点个star哦）

下面具体讲解以下实现的思路，大概需要解决的问题如下：

如何表示数组
如何得到随机采样数组，数组有无重复数据
如何实现排序算法
如何把数组可视化出来

一、如何表示数组

Python提供了list类型，很方便可以表示C++中的数组。标准安装的Python中用列表(list)保存一组值，可以用来当作数组使用，不过由于列表的元素可以是任何对象，因此列表中所保存的是对象的指针。这样为了保存一个简单的[1,2,3]，需要有3个指针和三个整数对象。对于数值运算来说这种结构显然比较浪费内存和CPU计算时间，再次就不详细论述。

二、如何得到随机采样数组，数组有无重复数据

假设我希望数组长度是100，而且我希望数组的大小也是在[0,100)内，那么如何得到100个随机的整数呢？可以用random库。

示例代码：

import randomdata = list(range(100))data = random.choices(data, k=100)print(data)[52, 33, 45, 33, 48, 25, 68, 28, 78, 23, 78, 35, 24, 44, 69, 88, 66, 29, 82, 77, 84, 12, 19, 10, 27, 24, 57, 42, 71, 75, 25, 1, 77, 94, 44, 81, 86, 62, 25, 69, 97, 86, 56, 47, 31, 51, 40, 21, 41, 21, 17, 56, 88, 41, 92, 46, 56, 80, 23, 70, 49, 96, 83, 54, 16, 36, 82, 24, 68, 60, 16, 98, 16, 81, 10, 13, 11, 24, 68, 35, 56, 39, 23, 44, 6, 30, 3, 60, 56, 66, 38, 28, 47, 47, 25, 90, 89, 38, 68, 21]

但是以上代码有个问题，random.choices是对一个序列进行重复采样，得到的数组存在重复数据，那如果不希望存在重复数据，而是希望进行无重复采样，怎么办？

可以用random.sample函数，示例代码：

data = random.sample(data, k=100)print(data)[49, 28, 56, 28, 44, 62, 81, 25, 48, 33, 54, 38, 30, 16, 13, 19, 23, 56, 60, 66, 41, 24, 68, 68, 77, 92, 78, 24, 66, 3, 80, 94, 78, 41, 84, 88, 21, 56, 25, 25, 75, 24, 38, 82, 31, 52, 23, 10, 71, 40, 27, 46, 33, 35, 56, 51, 1, 23, 12, 25, 89, 16, 21, 21, 11, 42, 47, 44, 81, 35, 86, 88, 29, 36, 77, 16, 39, 6, 57, 69, 96, 68, 24, 86, 97, 90, 69, 10, 68, 98, 56, 44, 83, 47, 70, 17, 47, 82, 60, 45]

这样就可以得到无重复采样数据了。

三、如何实现排序算法

算法种类较多，就不一一举例；再次就以希尔排序(Shell Sort)为例讲讲：

尔排序的原理：希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

基础的插入法排序是两重循环，希尔排序是三重循环，最外面一重循环，控制增量gap，并逐步减少gap的值。二重循环从下标为gap的元素开始比较，依次逐个跨组处理。最后一重循环是对组内的元素进行插入法排序。这样进行排序的优点在于每次循环，整个序列的元素都将小元素的值逐步向前移动，数值比较大的值向后移动。

示例代码：

from data import DataSeq
def ShellSort(ds):    assert isinstance(ds, DataSeq), "Type Error"
    Length = ds.length    D = Length//2    while D>0:        i=0        while i<Length:            tmp = ds.data[i]
            j=i            while j>=1 and ds.data[j-D]>tmp:                ds.SetVal(j, ds.data[j-D])                j-=D            ds.SetVal(j, tmp)
            i+=D        D//=2
if __name__ == "__main__":    ds=DataSeq(64)    ds.Visualize()    ds.StartTimer()    ShellSort(ds)    ds.StopTimer()    ds.SetTimeInterval(0)    ds.Visualize()

四、如何把数组可视化出来

有了随机数组初始化方法，再实现好排序函数，我们还差一步，就是把排序函数中每次移动数组后将数组可视化并输出。

对数组进行可视化，很容易想到Python的可视化工具matplotlib！但是在项目中我并没有用matplotlib，而是用了numpy+opencv。

为什么不用matplotlib？

因为在排序过程中，每次修改数组，都希望能够实时修改图片并输出，matplotlib确实很方便，但是matplotlib的效率实在是不高，而且每次修改数组前后的两幅图片其实是差不多的。如果用matplotlib，每次都是要重新绘制图片，非常耗时！！！

所以考虑自己生成图片，在每次修改数组后，只将图片中改动的那两列进行修改即可！这样就比用matplotlib每次重新绘制图片效率高得多！

数组中主要有两种操作，一种是对某个idx赋值，一种是交换某两个idx的值。

示例代码：

class DataSeq:    WHITE = (255,255,255)    RED = (0,0,255)    BLACK = (0,0,0)    YELLOW = (0,127,255)    def __init__(self, Length, time_interval=1, sort_title="Figure", repeatition=False):        pass    def Getfigure(self):        _bar_width = 5        figure = np.full((self.length*_bar_width,self.length*_bar_width,3), 255,dtype=np.uint8)        for i in range(self.length):            val = self.data[i]            figure[-1-val*_bar_width:, i*_bar_width:i*_bar_width+_bar_width] = self.GetColor(val, self.length)        self._bar_width = _bar_width        self.figure = figure    def _set_figure(self, idx, val):        min_col = idx*self._bar_width        max_col = min_col+self._bar_width        min_row = -1-val*self._bar_width        self.figure[ : , min_col:max_col] = self.WHITE        self.figure[ min_row: , min_col:max_col] = self.GetColor(val, self.length)    def SetVal(self, idx, val):        self.data[idx] = val        self._set_figure(idx, val)
        self.Visualize((idx,))
    def Swap(self, idx1, idx2):        self.data[idx1], self.data[idx2] = self.data[idx2], self.data[idx1]        self._set_figure(idx1, self.data[idx1])        self._set_figure(idx2, self.data[idx2])
        self.Visualize((idx1, idx2))