图神经常微分方程综述

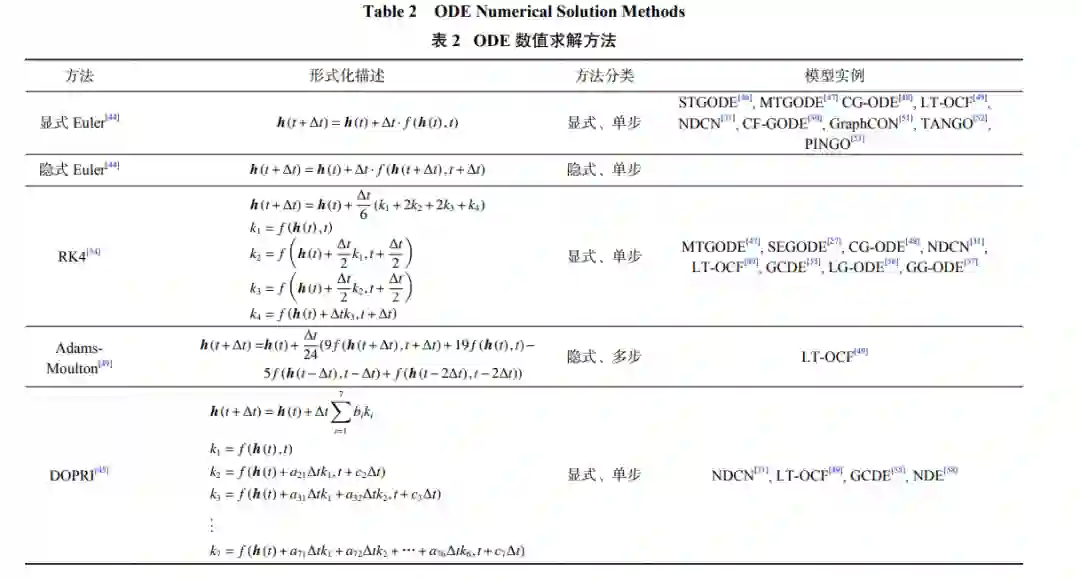
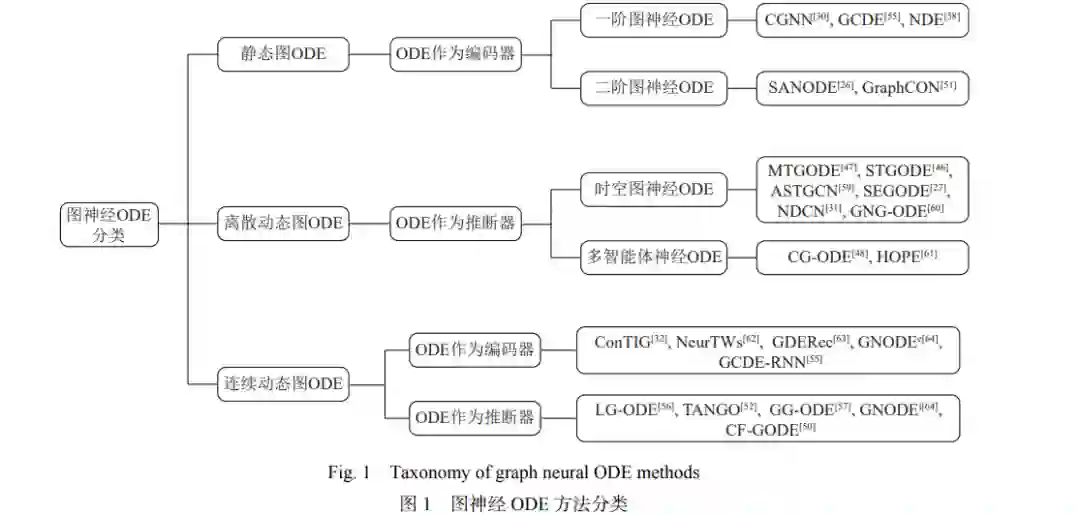
图神经网络（graph neural network，GNN）是处理图结构数据的强大工具，能够捕捉节点间的复杂关系和特征. 但GNN的离散架构导致其在表示图结构、建模图演化、适应不规则数据和计算开销等方面面临诸多挑战. 面对这些挑战，神经常微分方程（ordinary differential equation，ODE）由于能够模拟系统状态的连续变化，具备“连续深度”的编码和推断能力，被作为解决GNN面临挑战的全新方法而引入. 然而，神经ODE是为欧式结构数据设计的，无法直接捕捉图结构特性. 因此，提出了图神经ODE，一种将神经ODE与GNN结合的新架构，可以更好地适应图结构数据并充分利用其特性. 近年来，图神经ODE相关研究已经深入到图机器学习的各个方向中，引发了新的研究热潮. 在此背景下，适时地对图神经ODE研究前沿进行了系统性综述. 首先，回顾了GNN的关键优势和面临的诸多挑战，阐述了引入神经ODE并与GNN结合的理论基础和实践意义. 随后，详细介绍了图神经ODE的背景和基本概念，并提出了一种新颖的分类方法，在此基础上对当前的相关方法进行了全面描述. 然后，介绍了相关研究常用的验证方法，包括下游任务及数据集. 进一步，深入探讨了图神经ODE在多个实用领域上的应用. 最后，对图神经ODE面临的挑战和未来发展趋势进行了总结和展望.