【UCLA博士论文】利用语言模型推进数学推理：多模态和知识密集型视角，208页pdf

https://escholarship.org/uc/item/678864d8

数学推理是人类智能的关键组成部分，对于推动教育和科学发展至关重要。本论文深入研究了能够进行稳健数学推理的语言模型系统的发展，标志着实现通用人工智能的重要一步。我们引入了多模态和知识密集型基准来评估大型语言模型（LLMs）和视觉语言模型（VLMs）在真实世界中的推理能力，包括视觉信息、表格数据和科学领域。本论文通过提出新的预训练VLMs推动了该领域的发展。例如，PatchTrm引入了一种基于patch的跨模态Transformer模型用于抽象图表推理。我们还提出了创新的检索和工具增强算法，以提升LLMs的能力。值得注意的是，Inter-GPS是一个用于几何的神经符号求解器，展示了人类水平的性能，这是该领域的首次突破。此外，PromptPG开创了使用强化学习进行动态上下文示例选择，显著提高了LLMs的稳定性和准确性。另一个突破性贡献是Chameleon，这一模型将LLMs与外部工具集成，大大增加了其在现实应用中的灵活性和有效性。论文最后分析了在视觉上下文中的最新数学推理进展，并强调了当前的挑战和未来前景。

数学推理是人类智能的基本方面，使我们能够理解和基于数据信息和语言做出决策。它适用于包括科学、工程、金融和日常生活在内的各个领域，涵盖了从基本技能如模式识别和数值运算到更高级技能如问题解决、逻辑推理和抽象思维的一系列能力。开发能够解决数学问题和证明定理的人工智能（AI）系统一直是机器学习和自然语言处理（NLP）研究的重点，追溯到20世纪60年代 [Fei63, Bob64]。 随着深度学习不断革新NLP任务，如问答和机器翻译 [SVL14, KT19]，它在数学推理方面也取得了显著进展 [WLS17, YD19, GGB20, WWS22b]。最近，大型语言模型（LLMs）如GPT-4 [Ope23a]和LLaMA 3 [TLI23]展示了令人印象深刻的数学推理能力，在GSM8K [CKB21]等基准上达到了接近人类水平的表现。 然而，目前的研究面临几个挑战。首先，研究主要集中在纯文本领域 [CKB21, HBK21]，而现实世界中的数学和科学问题通常涉及多模态上下文，如图像、图表和表格。其次，LLMs在某些文本基准上的表现趋于饱和，改进空间有限 [Ant24, ZWL23]。第三，在需要检索和应用领域知识、进行多步骤推理和使用特定领域工具的更复杂的现实挑战上，仍存在显著的性能差距 [LBX24]。

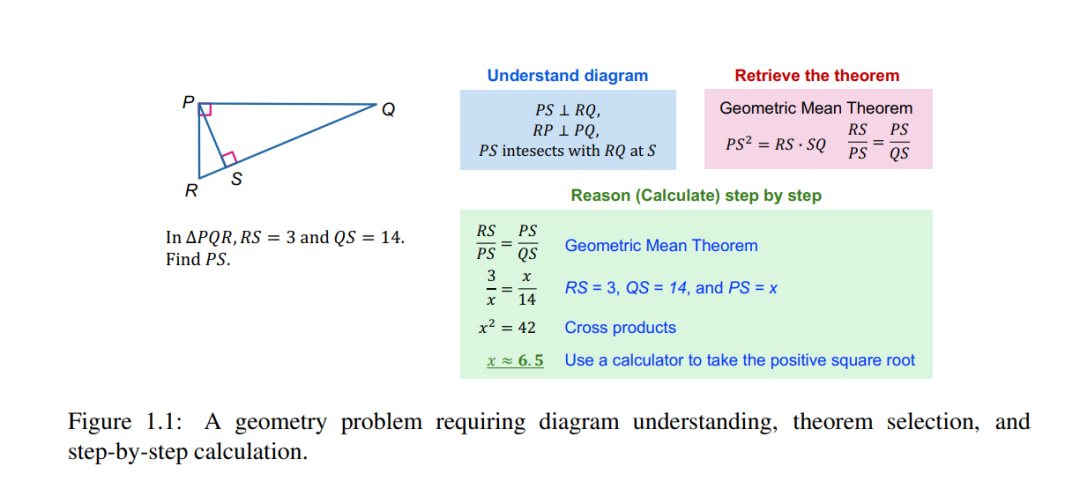
数学推理是人类智能的基本方面，使我们能够理解和基于数据信息和语言做出决策。它适用于包括科学、工程、金融和日常生活在内的各个领域，涵盖了从基本技能如模式识别和数值运算到更高级技能如问题解决、逻辑推理和抽象思维的一系列能力。开发能够解决数学问题和证明定理的人工智能（AI）系统一直是机器学习和自然语言处理（NLP）研究的重点，追溯到20世纪60年代 [Fei63, Bob64]。 随着深度学习不断革新NLP任务，如问答和机器翻译 [SVL14, KT19]，它在数学推理方面也取得了显著进展 [WLS17, YD19, GGB20, WWS22b]。最近，大型语言模型（LLMs）如GPT-4 [Ope23a]和LLaMA 3 [TLI23]展示了令人印象深刻的数学推理能力，在GSM8K [CKB21]等基准上达到了接近人类水平的表现。 然而，目前的研究面临几个挑战。首先，研究主要集中在纯文本领域 [CKB21, HBK21]，而现实世界中的数学和科学问题通常涉及多模态上下文，如图像、图表和表格。其次，LLMs在某些文本基准上的表现趋于饱和，改进空间有限 [Ant24, ZWL23]。第三，在需要检索和应用领域知识、进行多步骤推理和使用特定领域工具的更复杂的现实挑战上，仍存在显著的性能差距 [LBX24]。 为了说明当前大型语言模型（LLMs）面临的挑战，我们考虑三个涉及几何图、科学场景和表格上下文的示例问题。解决图1.1中的几何问题需要理解图表、解释符号和属性，并应用适当的定理，如几何平均定理。虽然乍看之下可能会应用毕达哥拉斯定理，但这会导致一个复杂的方程系统。相反，几何平均定理通过建立一个简单的方程并逐步计算，可以更直接地解决问题。 图1.2提出了一个科学问题，需要理解婴儿打开柜门的多模态情境，回忆相关背景知识，并基于情境和知识提供逐步推理以得出正确答案。图1.3展示了两个在表格上下文中的数学文字题。第一个问题要求计算一组数的中位数，需要回忆如何计算中位数，并可能利用Python解释器以获得精确结果。第二个问题涉及更大的表格，可以通过使用行查找工具来定位相关信息，从而简化问题。 解决这些问题需要超越仅处理文本的能力，例如理解视觉信息、检索相关知识和进行严格的逻辑推理，可能还需要外部工具的帮助。当前的LLMs虽然强大，但并不适合处理这些需要复杂推理的多模态、知识密集型问题。

为了解决这些挑战，本论文首先提出了多模态、知识密集型基准来评估LLMs在真实世界数学和科学问题上的能力。这些基准旨在： （1）多模态，包含不仅是文本，还有自然图像、几何图、抽象场景和科学图表；（2）知识密集型，需要检索和应用领域知识、在线资源、教科书、定理和规则；（3）需要严格的多步骤推理，通常需要神经符号推理、工具增强和验证以确保预测的精确性。 本论文随后探索了预训练的视觉语言模型（VLMs），通过预训练和分层图像解析布局来增强数学推理能力。此外，还提出了工具增强和检索增强算法，显著提升了LLMs在实际场景中的数学推理能力。关键见解包括：（1）整合形式语言和符号求解器可以加强LLMs在几何等复杂推理方面的能力；（2）LLMs可以学习动态选择相关示例，以提高上下文学习性能；（3）LLMs可以有效利用外部工具和资源。 最终目标是开发LLMs及其视觉变种VLMs，使其能够更加稳健和灵活地应用数学推理，通过多模态理解、检索和应用相关知识、组合必要的工具，并通过可解释的多步骤推理生成正确的解决方案，以解决各个领域的实际问题。本论文通过新的基准、模型和算法向这一目标迈出了重要步伐，同时揭示了该领域的关键挑战和未来机遇。