武器-目标分配问题是组合优化中的一个经典任务分配问题,其目标是将一定数量的工人(武器)分配给一定数量的任务(目标)。解决这一问题的经典方法通常使用集中式规划器,这会导致单点故障,而且往往无法在条件发生变化时进行实时重新规划。本文介绍了一种由武器执行分布式自主任务规划的新方法,其中每个武器负责对决策变量的不同子集进行优化。本文介绍了相关成本函数和约束条件的连续凸松弛,并开发了一种分布式基元-二元优化算法,该算法即使在异步计算和通信的情况下也能保证收敛速度。这种方法在实践中具有若干优势,因为它对异步具有鲁棒性,对时变场景具有弹性,这些优势在使用模拟和物理商用现成地面机器人作为武器代理的实验中得到了展示,实验表明,这些机器人能在通信间歇和武器意外损耗(丢失)的情况下成功计算其任务。
自 1958 年首次提出[1]以来,武器-目标分配(WTA)问题一直是组合优化和更广泛的运筹学领域中研究得很透彻的问题[2-5]。给定一组已知概率有效性的武器和一组已知价值的目标,WTA 问题寻求以最小化所有幸存目标交战后期望值的方式将每种武器分配给一个目标。这个问题显然适用于军事规划人员,但也被用于许多其他资源分配问题,如应急管理 [6] 和广告 [7](与之相似)。自 1986 年以来,WTA 问题一直被认为是 NP-完全问题[8],因此成为研究复杂度更低的启发式优化算法的沃土[9-11]。虽然 WTA 问题的一般结构可以有很多变化,如部分信息 WTA [12],包含目标、武器和反武器的多层问题 [13],包含目标识别、验证和交战的多任务实现 [14],或顺序交战 WTA [15,16],但本文将侧重于扩展经典问题的表述。关于 WTA 问题的精确方法和启发式方法的概述,读者可参阅 [17]。WTA 的最初形式是准静态的,即目标及其值在整个交战过程中不会改变,武器的属性也不会改变。最初的解决方案(以及之后的许多解决方案)也是集中式的,即由一个规划者计算所有武器分配。
虽然集中规划可能非常适合某些情况,例如非自主空对地弹药,但现代和未来的弹药有能力自主规划和行动,这意味着不需要集中规划。事实上,这可能无法充分发挥单个武器的决策能力。此外,集中式预规划在静态条件下可能会很有效,但如果出现意外变化,如武器损耗(飞行过程中丢失),通常需要重新规划,而重新规划可能会因计算负担而耗费大量时间。重新规划也很难进行集中协调,因为当武器已经部署完毕且分布较远时,很难与它们进行沟通和协调。有算法表明,在某些集中式和分布式方法都可行的情况下,分布式方法的性能明显更好[18]。虽然 WTA 问题很容易以集中的方式指定,但现代自主应用越来越多地发生在未知、非结构化和有争议的环境中,所有这些都表明,使用集中式规划器要么不可行,要么不可取,因为它会造成单点故障,无法对不断变化的条件做出快速反应。
特别是,所谓的 "开火即忘 "方法无法实现动态变化的武器分配,这就不允许武器在部署过程中改变方向,也不允许武器对其他武器实现目标的成败做出反应。鉴于 WTA 规划是概率性的,这种缺乏反应能力的情况可能会导致使用的武器数量超过需要。例如,假设在规划时为一个目标分配了几种武器,以达到预期的成功概率。前一、两种武器可能会在运行时摧毁目标,但由于缺乏重新规划,其他武器将按计划继续攻击已被摧毁的目标。同样,如果预计武器会损耗,那么可能会分配五种武器同时到达一个目标,而实际上只需要两种武器就能到达目标以实现任务目标。如果在运行初期没有武器损耗,那么重新分配多一种武器可能会有好处,但 "发射后即忘 "的方法不具备这种能力。无法即时重新规划还意味着,武器无法根据分配给其他优先级更高的目标的武器的损耗情况(如事故或敌方反制措施造成的损耗)来修改其任务分配,所有这些也都可能导致不良结果。避免这种低效率的方法之一是设计一种在线算法,通过重新分配武器对不断变化的条件做出反应,但标准的集中式方法在现实条件下无法做到这一点。
近年来,控制理论[19]、优化[20]和其他领域[21]对分布式决策系统产生了浓厚的兴趣。分布式系统的优势在于,它不需要一个集中的协调者来让每个智能体采取行动。相反,智能体利用点对点的互动进行决策。有多种方法将 WTA 问题纳入分散式框架,如进化算法 [22]、博弈论公式 [23]、并行模拟退火 [20]、蚁群算法 [24]、启发式方法 [25]、嵌套分区 [26]、混合整数线性规划 [27] 和拍卖算法 [28]。此外,分布式方法还用于自主武器系统的其他组成部分,如同时拦截目标[29]和避免碰撞[30],这表明分布式任务分配算法可纳入整体控制框架。虽然针对特定类别的问题 [38] 或有限的异步模型 [39] 开发了用于受限优化问题的分布式算法,但许多异步算法仅适用于无约束问题的表述 [40, 41]。因此,我们需要一种易于分发的 WTA 问题表述,以及一种能够容忍异步并解决更一般形式的受限优化问题的算法。
鉴于分布式方法的优势,本文为 WTA 问题开发了一种分布式求解器,该求解器消除了对中央协调器的任何依赖,并提供了根据武器损耗情况即时重新规划的能力。本文的贡献包括:a) 对经典 WTA 问题进行了连续凸松弛;b) 开发了一种分布式算法,可容忍任意大的有界延迟;c) 推导了明确的收敛率,约束了与松弛问题解的距离;d) 演示了模拟和硬件环境下的结果。具体来说,本文的优势在于明确考虑了智能体之间异步通信和计算所固有的实际挑战。首先,本文提出了经典 WTA 问题的连续凸松弛,从而可以使用凸优化技术来解决该问题。然后,针对松弛后的约束凸优化问题开发了一种分布式算法。该算法是一种一阶分布式的原始-对偶算法,所有原始通信和计算都允许异步进行,而对偶更新则需要偶尔进行一些协调。与所有智能体更新所有决策变量的基于平均法的现有方法[31-37]不同,该算法解决的是不等式约束的问题,并采用基于块的更新法[31, 42-44],其中每个原始变量和每个对偶变量只由一个智能体更新。据我们所知,该类方法中唯一允许异步的现有方法是两位作者的早期工作 [45, 46]。本文对这项工作进行了扩展,消除了收敛过程中的持续误差,并适应了目标函数不具有对角主导赫西矩阵的问题(如本文推导的问题)。收敛率的推导约束了该算法到松弛问题拉格朗日鞍点的距离,而该点提供了原始问题的解决方案。实验中使用了商用现成(COTS)地面机器人和模拟地面机器人作为武器代理。结果表明,无论是在静态条件下,还是在武器根据武器损耗情况通过更新损耗发生前计算出的最优或次优分配而进行实时重新规划的情况下,该算法都取得了成功。
本文结构如下。第二节是经典 WTA 问题表述的初步介绍。第三节是经典 WTA 问题表述的连续凸松弛推导。第四节介绍分布式算法并推导收敛率。最后,第六节是结论,并提出了未来研究的可能方向。
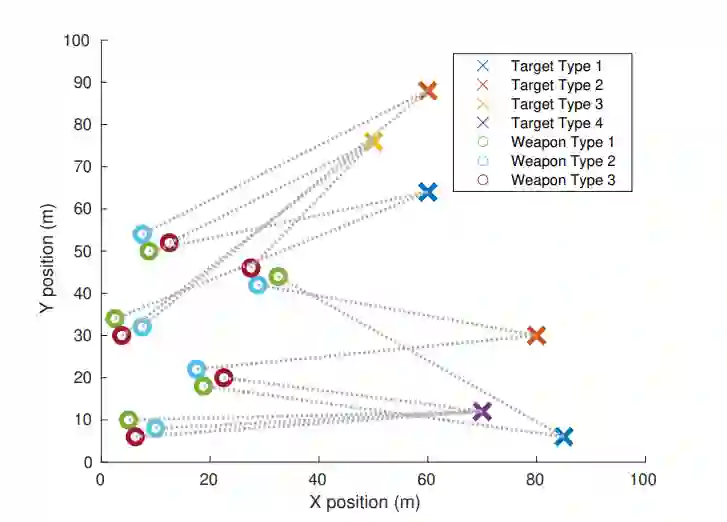
图 5 均质场景中武器和目标的初始位置。灰色虚线表示最终的武器-目标分配。