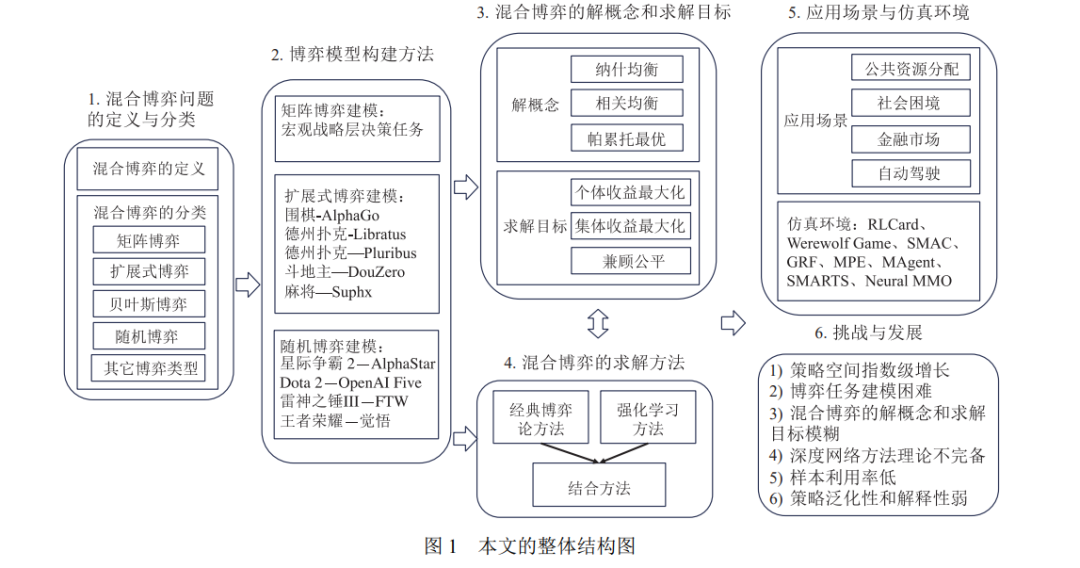
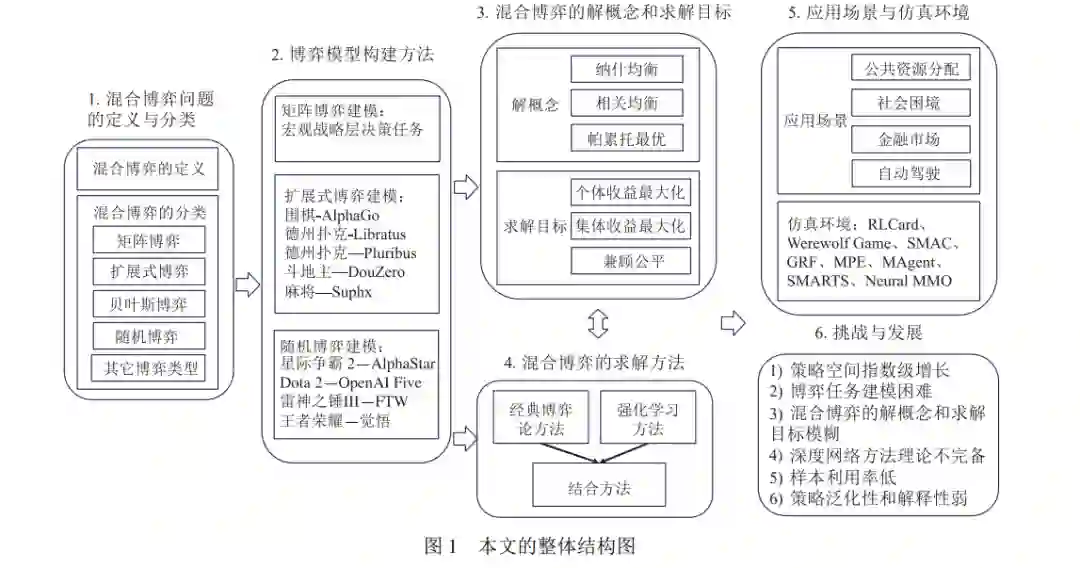
近年来, 随着人工智能技术在序贯决策和博弈对抗等问题的应用方面取得了飞速发展, 围棋、游戏、德扑 和麻将等领域取得了巨大的进步, 例如, AlphaGo、OpenAI Five、AlphaStar、DeepStack、Libratus、Pluribus 和 Suphx 等系统都在这些领域中达到或超过人类专家水平. 这些应用集中在双人、两队或者多人的零和博弈问题中, 而对于混合博弈问题的研究缺乏实质性的进展与突破. 区别于零和博弈, 混合博弈需要综合考虑个体收益、集体 收益和均衡收益等诸多目标, 被广泛应用于公共资源分配、任务调度和自动驾驶等现实场景. 因此, 对于混合博弈 问题的研究至关重要. 本文通过梳理当前混合博弈领域中的重要概念和相关工作, 深入分析国内外研究现状和未 来发展方向. 具体地, 本文首先介绍混合博弈问题的定义与分类; 其次详细阐述博弈解概念和求解目标, 包含纳什 均衡、相关均衡、帕累托最优等解概念, 最大化个体收益、最大化集体收益以及兼顾公平等求解目标; 接下来根 据不同的求解目标, 分别对博弈论方法、强化学习方法以及这两种方法的结合进行详细地探讨和分析; 最后介绍 相关的应用场景和实验仿真环境, 并对未来研究的方向进行总结与展望.
博弈论 (game theory) 最早在 17 世纪由数学家们构想出来解决赌博、象棋和双人纸牌游戏等零和博弈 (zerosum game) 问题. 20 世纪 50 年代, 博弈论由 Von Neumann 和 Morgenstern 正式提出, 出版了博弈论领域的著作 《博弈论与经济行为》(Theory of Games and Economic Behavior)[1] . 随着时间的推移, 博弈论逐渐扩展到非零和博 弈, 即多方参与并且可以共同获益的情况. John Nash 提出了纳什均衡的概念, 即在博弈中每个参与者都选择最优 策略时, 没有人可以通过改变自己的策略来获得更高的收益[2] . 随后, 随着博弈论专家的深入研究产生了许多重要 的概念, 如合作博弈[3]、子博弈[4]和重复博弈[5]等. 博弈论的应用领域非常广泛: 在经济学中, 博弈论被用于研究市 场竞争、拍卖和定价等问题; 在政治学中, 博弈论被用于分析选举、多方合作与地缘冲突等行为; 在生物学中, 博 弈论被用于研究物种进化中的合作与竞争策略. 此外, 博弈论还被应用于社会科学、计算机科学和工程学等领域. 总的来说, 博弈论的发展与应用历程丰富, 它为我们理解和解决多智能体系统 (multi-agent system, MAS) 决策问题 提供了重要的工具和思维方式. 近年来, 人工智能 (artificial intelligence, AI) 和博弈论技术已经被成功应用在各种任务中, 包括游戏场景、军 事作战和工业控制等. 在以上案例和应用中, 以围棋[6][7]、德扑[8][9][10]、麻将[11]、星际争霸[12]、Dota 2[13]、王者荣 耀[14]和军事作战等为代表的双人零和或两队 (多人) 零和博弈问题, 现有方法往往通过蒙特卡洛树搜索、深度强 化学习 (deep reinforcement learning, DRL) 和自博弈 (self-play) 等技术, 将人工智能和博弈论方法相结合, 最终使得 智能体在以上场景中的表现能够达到或超过人类专家水平. 其次, 在网络路由[15][16]、交通指挥[17][18]、机器人控 制[19] , 和包括先前介绍的星际争霸多智能体挑战[20]、谷歌足球研究[21]等多智能体游戏对抗中的某一方或一队, 这 类场景中往往是双人或多人的合作博弈 (cooperative game) 问题, 所有智能体会共享一个全局的奖赏函数, 需要通 过合作完成一个共同目标. 而在一般的混合博弈 (mixed-motive game) 场景下, 包括公共资源分配[22][23][24]、任务调度[25]和自动驾驶[26][27] 等应用, 不同于合作博弈问题, 此类问题中每个智能体都有独立的奖赏函数, 例如上述应用中的每个智能体分配调 度的资源、行驶时间等, 因此整个系统既要考虑智能体自身的收益, 也要考虑系统的总体收益, 还要兼顾公平, 最 终建立某种均衡准则和社会规范使系统维持稳定. 虽然混合博弈场景更加贴近于现实生活, 但现有的研究工作缺 乏系统性的认识和实质性的突破. 例如, 对于该博弈问题解的定义与性质分析仍然沿用传统博弈的解概念, 缺乏对 混合博弈特定问题的考虑; 以强化学习 (reinforcement learning, RL) 和博弈论为代表的方法对数学形式化的博弈模 型和求出的收敛解没有清晰的范围和界定. 因此, 混合博弈问题亟待开展广泛研究. 目前, 已有诸多对多智能体系统、多智能体强化学习 (multi-agent reinforcement learning, MARL) 和博弈论相 关的综述文章, 涉及内容也非常广泛. 首先, 关于多智能体系统的研究方向, 多智能体系统没有一个被普遍接受的 定义, 在这个问题上有很多正在进行的辩论和争议[28] . 目前只能给出一些较为宽泛的定义: 多智能体系统是由多 个相互作用的智能体追求某组目标或执行某组任务的系统, 这些智能体要么具有不同的信息, 要么具有不同的利 益, 或者两者兼而有之[28][29] . 其次, 一些文章认为多智能体系统是分布式人工智能 (distributed artificial intelligence, DAI) 的一个子领域, 包括对智能体的架构、通信、协同、决策和学习能力的研究[30][31] . 另外, 一些与人工智能和 机器学习结合的多智能体系统相关综述工作讨论了智能体同构或异构的结构, 以及智能体之间是否能够进行通 信[32] , 而另一个工作则提出了著名的五种 AI 算法议程 (agenda): 包括计算型、描述型、标准型、规定的合作型和 非合作型[33] . 第二, 关于多智能体强化学习的研究方向, 相关工作对多智能体强化学习的目标和算法分类进行了综述, 分别讨论了基于值和基于策略的方法在完全合作型、完全竞争型以及混合型任务上的应用[34] , 后续相关文 章又针对两种经典的扩展式博弈和随机博弈对多智能体强化学习的理论收敛性进行分析, 特别是之前工作很少涉 及的扩展式博弈中的学习, 带有网络连接的独立式学习, 平均场状态下的多智能体强化学习, 基于策略的学习方法 等的收敛性分析[35] . 在深度学习技术引入后, 又有许多综述文章对部分可观测环境[36]、环境非稳定性[37]、迁移学 习[36][38]、强化学习可解释性[39]和强化学习探索[40]等专题进行了细致的梳理和总结. 具体来说, 部分可观测的环境 表示与环境相关的完整状态信息在智能体与环境交互时是不知道的. 在这种情况下, 智能体只能观测到环境的部 分信息, 并且需要在每个时间步上做出最佳决策, 这类问题通常用部分可观测的马尔可夫决策过程建模[36] . 针对 环境非稳定性问题, 从复杂度不断增加的角度, 目前方法可以通过忽视、遗忘、回应对手、学习对手模型和递归 推理的心智理论等方式进行解决[37] . 强化学习中关于迁移学习问题的综述, 包含了对任务差异的假设、源任务的 选择、任务映射、迁移知识和允许的强化学习算法等五种维度的分类[38] . 强化学习可解释性的综述文章, 定义了 解释的含义、讨论影响可解释性的因素、划分解释的直观性, 然后根据强化学习的特性, 将解释的内容划分为环 境解释、任务解释和策略解释[39] . 最后, 为了解决强化学习中样本效率低下的问题, 强化学习探索的综述文章从 单智能体和多智能体强化学习的角度对当前探索方法划分为不确定性导向探索和内在动机导向探索两个方面进 行分析[40] . 近年来, 针对博弈论和多智能体强化学习技术相结合的综述文章也分析了两者的起源[41] , 并且在多智 能体系统中的行为涌现、智能体建模、学习合作和学习通信等方面总结目前多智能体强化学习的方法, 然后从延 时反馈奖赏、自博弈和组合维度灾难等方面的挑战分析强化学习、多智能体强化学习和多智能体学习 (multiagent learning, MAL) 之间的关系[42] . 最后一些综述文章总结了相关方法在零和博弈[43]、合作博弈[44]、混合博弈[45]、 势博弈[46]、平均场博弈[46]等不同博弈类型中的应用. 相关综述文章的分类与描述如表 1 所示. 但是, 以上综述文章缺乏对混合博弈特定解概念和求解目标的拓展, 缺乏对不同求解方法的侧重和针对任务 类型的描述, 缺乏对相关数学形式化博弈模型和收敛解联系与区别的讨论. 因此, 本文对混合博弈问题进行系统性 地梳理和分析, 以博弈基础理论为核心, 结合目前的研究现状和发展趋势, 重点介绍混合博弈问题的定义与分类, 研究从现有复杂环境到经典博弈问题的建模方法, 构建状态动作表征、奖赏函数和支付矩阵的定义方法等. 然后 深入分析混合博弈问题中的解的概念与性质、总结以经典博弈论、强化学习以及两者结合的求解方法和实际应 用, 最后对未来研究方向进行总结与展望.