【ICML2025】时序分布漂移下的自适应估计与学习

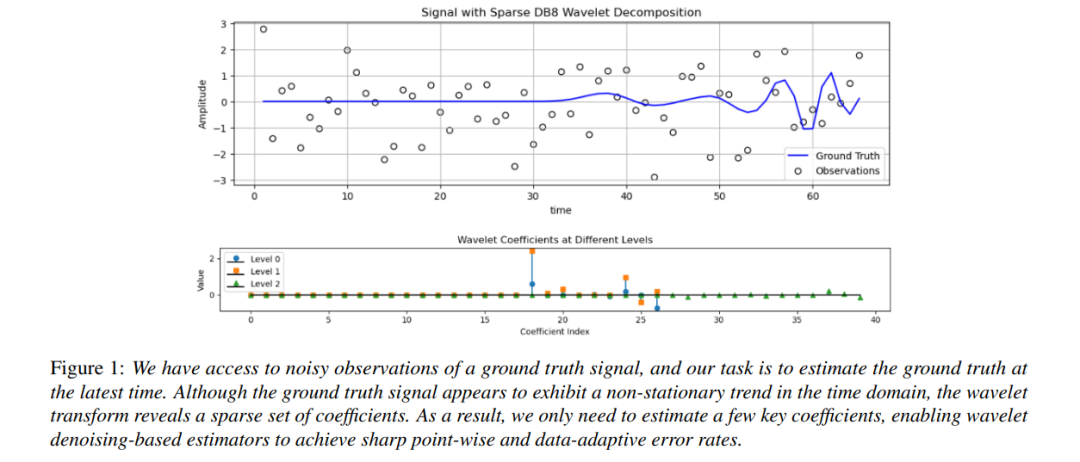
在本文中，我们研究了时序分布漂移（temporal distribution shift）下的估计与学习问题。考虑一个长度为 nnn 的观测序列，它是某个时变真实序列的带噪实现。我们的核心目标是估计该真实序列在最终时刻的值，同时提供具有严格精度保证的逐点估计误差界。

我们证明，即使在对时序漂移程度没有先验知识的情况下，小波软阈值估计器（wavelet soft-thresholding estimator）也能实现对真实值的最优误差界。我们提出的估计方法推广了 Mazzetto 和 Upfal（2023）的研究成果，通过建立序列的非平稳程度与其小波变换域中的稀疏性之间的联系，实现了理论上的突破。

我们的理论结果得到了数值实验的验证。此外，我们还将该估计器应用于分布漂移下的二分类问题，推导出具有稀疏性意识的超额风险界（sparsity-aware excess risk bounds），并设计了计算效率高的训练目标函数。作为最后的贡献，我们将所得结果与经典信号处理中的全变差去噪（total variation denoising）问题（Mammen 和 van de Geer, 1997；Tibshirani, 2014a）进行了类比，进而发现了适用于该任务的全新最优算法。