【MIT博士论文】分层概率多模态数据融合研究进展，289页pdf

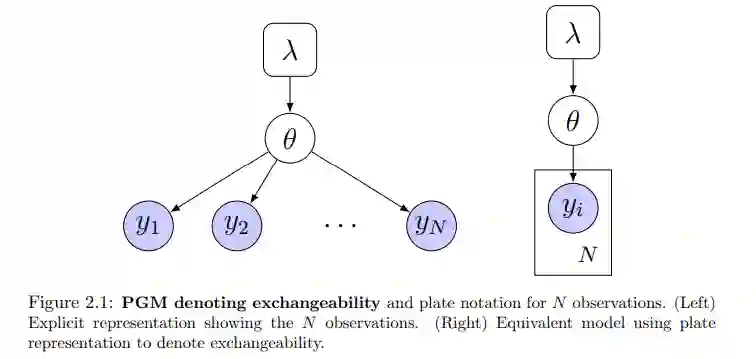
多模态数据融合是将不同的数据源集成到一个适用于复杂推理的共享表示的过程。因此，人们可以对潜在现象做出比单独使用每个数据源更精确的推论。在论文中，我们采用贝叶斯观点的多模态数据融合，它将推理定义为对潜在变量的后验推理。在贝叶斯设置中，我们提出了一种新的数据集成方法，我们称之为轻量级数据融合(LDF)。LDF解决了数据源子集的正向模型未知或特征不佳的情况。LDF利用剩余的数据源学习适合后验推断的逆模型，该模型结合了这两种类型的数据。此外，我们开发了分层Dirichlet过程(mmHDPs)的多模态扩展，其中，与LDF的设置相比，我们缺乏跨模态的观察级对应，数据来自隐式潜在变量模型。最后，我们为Dirichlet过程和HDP混合模型开发了一种新颖的表示，可以在推理过程中实现并行化，并扩展到更复杂的模型，包括mmHDPs。

我们解决数据融合的问题，即从多个数据源学习。我们考虑了几个具体的挑战:例如，某些数据源可能缺乏特征良好的正向模型，或者底层模型的复杂性可能未知。我们采用贝叶斯视角，将数据融合问题视为对潜在变量结构的后验推断，并允许进行各种分析，包括不确定性量化、优雅地处理缺失数据和模型检查。然而，贝叶斯推断也提出了自己的挑战。后验推断的常见方法不适应缺乏前向模型或难以适应大数据集的观察模式。

本论文的一个重要重点是开发能够实现高效和并行的后验推理的表示。我们特别关注多模态数据融合中的两个明显挑战。首先，当一个或多个观察模态缺乏特征良好的前向模型，并且我们也缺乏明确标记的训练数据，从而允许直接学习前向模型时，我们考虑学习。在这里，我们使用了来自不同模态的数据，它具有一个特征良好的正态模型，与未校准的数据一起出现。我们提出了一种方法，该方法使用具有良好校准数据的联合观测来学习一种模态的逆模型。其次，我们试图从多种测量模态中学习，其中跨模态的观察之间的直接对应是不可用的。我们利用不同模态的数据组之间的对应关系来揭示共同表示。在这里，我们开发了层次Dirichlet过程(HDP)混合模型的扩展，将不同的模态表示为子文档。本文解决了这两个问题，并开发了一种新的Dirichlet过程(DP)和HDP混合模型的表示，从而产生了一个并行推理过程。

在第三章中，我们提出了轻量级数据融合(LDF)。LDF是一种基于多源数据的贝叶斯推理新方法，其中一些源缺乏已知的正演模型。虽然与论文中的其他章节略有不同，但LDF确实解决了多模态数据融合中的一个常见挑战。LDF的一个核心组成部分是它将未校准的数据源简化为一组描述后验分布的信息统计数据。我们为一般的模型结构制定了LDF，并表明我们的构造导致了有效的推理和一个易于处理的学习过程，具有吸引人的信息理论属性。LDF使用具有已知可能性的数据类型来帮助学习如何对具有未知可能性的数据类型设置条件。

在第四章中，我们开发了一种新的DP和HDP混合模型的表示，这对设计高效的推理程序有重要的意义。在本章中，我们假设数据的正向模型是已知的，与第3章不同;我们将使用在第5章中开发的方法。特别地，我们引入了DP和HDP混合模型的聚合表示，它们既有被实例化的显式原子，也有被聚合成未实例化组件的隐式原子。未实例化组件是延迟实例化Gibbs采样器的核心，它允许并行执行许多采样操作。

我们在第5章中介绍了DP和HDP混合模型的扩展，它可以容纳多个数据源，并允许学习联合依赖。在第4章中，我们假设数据的正向模型是已知的。本章使用底层的泊松过程表示定义了多模态DP和HDPs，并将它们用作混合模型的基础。所得到的模型可以被视为所有模态的联合措施，也可以被视为适用于单个模态的边际随机措施。我们提供了这些模型的几种特征，指定了折叠推理过程，并使用第4章中的延迟实例化开发了一个并行推理过程。