NeurIPS 2022最新「贝叶斯优化」教程报告，230+页PPT阐述BO最新进展

作为目前全球最负盛名的人工智能盛会之一，NeurIPS (Conference on Neural Information Processing Systems) 在每年年末都是计算机科学领域瞩目的焦点。被 NeurIPS 接收的论文，代表着当今神经科学和人工智能研究的最高水平。今年的 NeurIPS 大会将于11月28日至12月9日举行，本届大会共收到10411篇有效投稿，其中2672篇获接收，最终接收率为25.6%。相比去年，投稿数量继续增加。大会涵盖了众多最近研究Tutorial报告，来自Jana Doppa等学者共同做了关于贝叶斯优化的进展报告，非常值得关注!

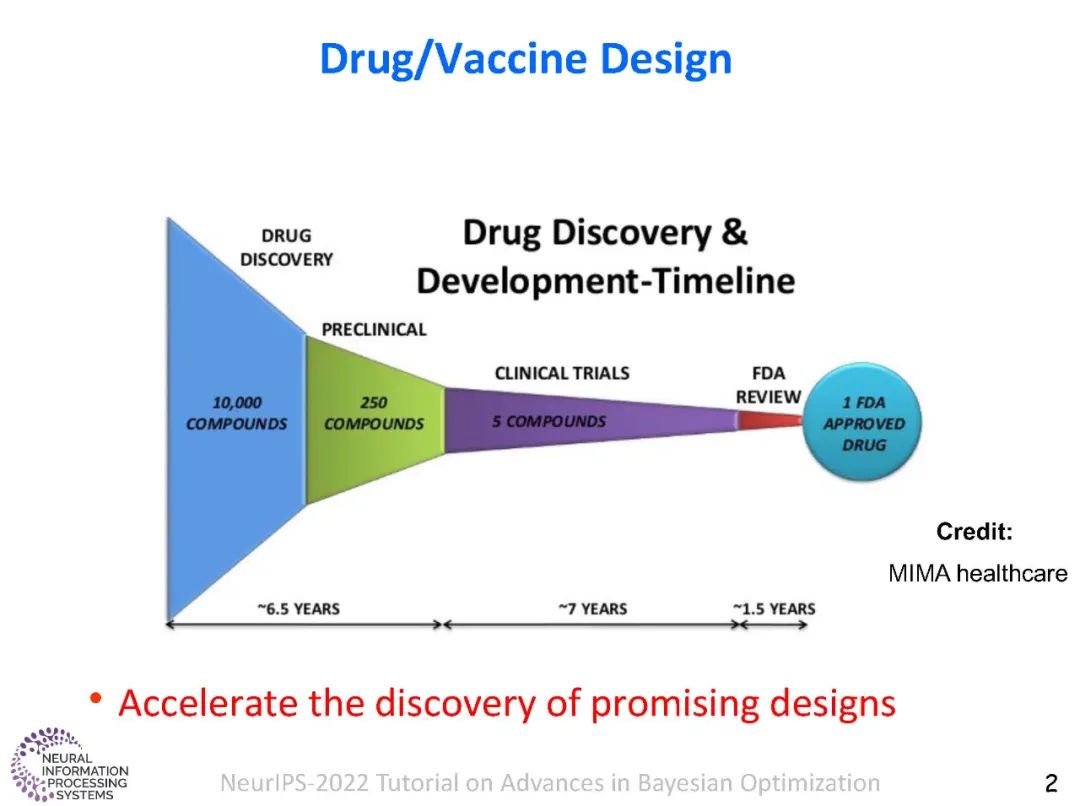
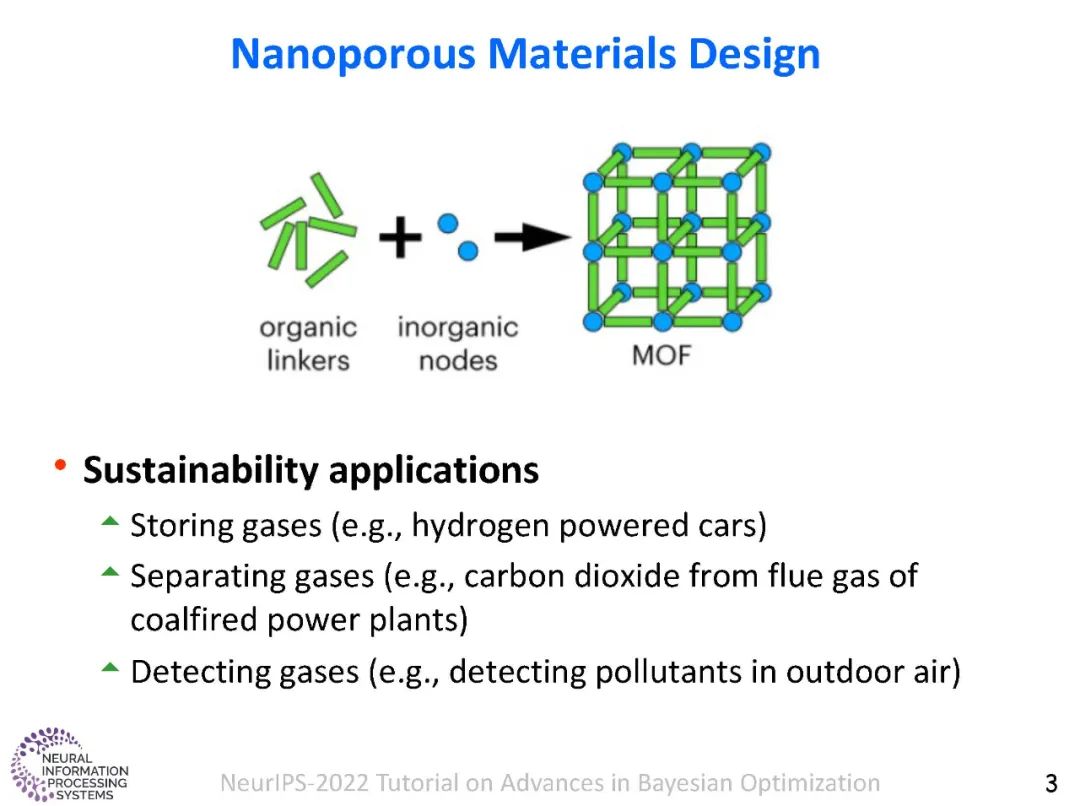
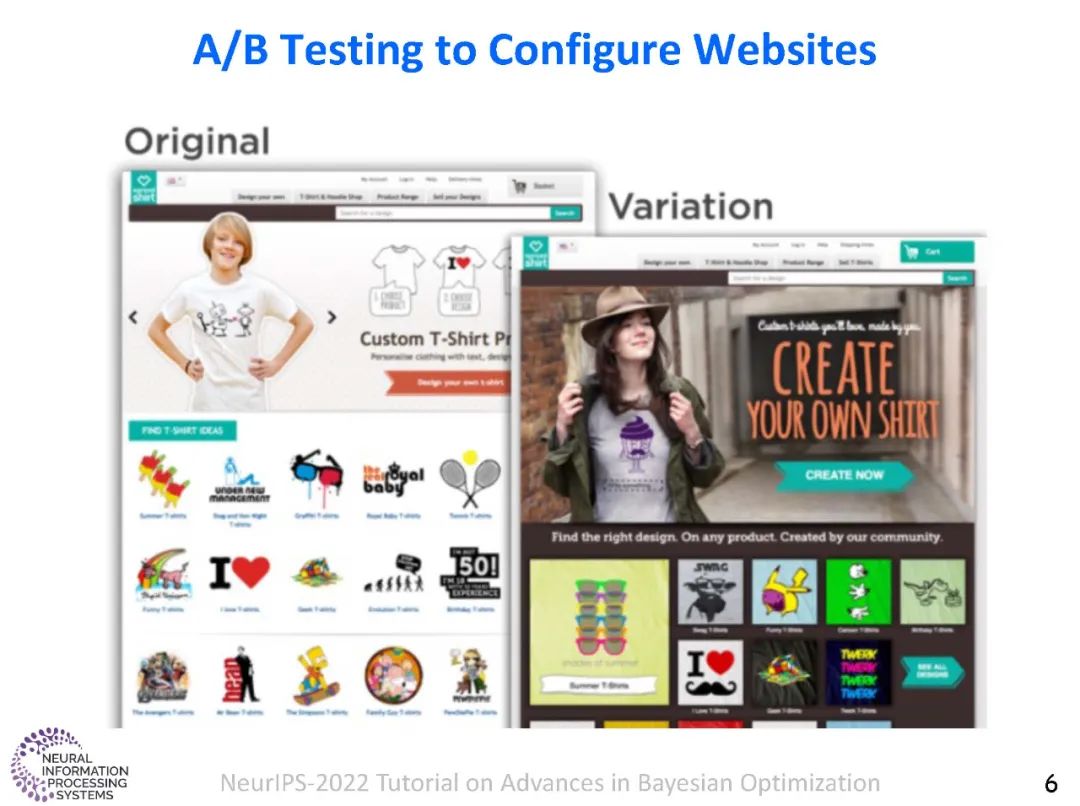
许多工程、科学和工业应用，包括自动机器学习(如超参数调优)，都涉及到设计选择，以优化一个或多个评估目标所需的成本。一些例子包括调整编译器的旋钮以优化一组软件程序的性能和效率;设计新材料以优化强度、弹性和耐久性;设计硬件以优化性能、功率和面积。贝叶斯优化(BO)是一种解决黑盒优化问题的有效框架。BO背后的关键思想是使用真实的实验数据建立一个廉价的代理模型(例如，高斯过程);并利用它智能地选择功能评估的序列，使用一个获取函数，例如，预期改善(EI)。

贝叶斯优化。BO是一种利用概率代理模型(通常是高斯过程(GP) Rasmussen(2003))进行样本高效黑盒优化的方法，它是一种利用代理找到最有希望的候选对象进行下一步评估的获取函数。BO是一种迭代进行的顺序优化算法。在每次迭代中，一个代理模型被训练从评估黑盒目标函数中收集的数据。根据代理模型的预测后验定义获取函数，然后最大化获取函数，选择一个或多个候选对象进行下一步评估，权衡探索和利用。

本教程的目标是通过关注BO的挑战、原则、算法思想和它们之间的联系，以及重要的现实世界应用，介绍BO的最新进展。具体来说，我们将介绍最近在获取函数、离散和混合空间的BO方法、高维输入空间的BO方法、因果BO和BoTorch工具箱中的关键创新以及实际演示方面的工作。

https://bayesopt-tutorial.github.io/

讲者：

目录内容：

Part I

BO框架和GPs的快速概述 Quick Overview of the BO Framework and GPs * GPs及采集功能进展综述 Summary of advances in GPs and Acquisition Functions * 离散/混合空间上的贝叶斯优化 Bayesian Optimization over Discrete/Hybrid Spaces

Part II

高维贝叶斯优化 High-Dimensional Bayesian Optimization * BoTorch Hands-on Demonstration

Part III

因果贝叶斯优化 Causal Bayesian Optimization * Summary and Outstanding Challenges in BO

参考文献：

General introduction and survey

Garnett, R. (2022). Bayesian Optimization. Cambridge University Press. Link * Shahriari, B., Swersky, K., Wang, Z., Adams, R. P., & De Freitas, N. (2015). Taking the human out of the loop: A review of Bayesian optimization. Proceedings of the IEEE, 104(1), 148-175. Link * Frazier, P. I. (2018). A tutorial on Bayesian optimization. arXiv preprint arXiv:1807.02811. Link * Greenhill, S., Rana, S., Gupta, S., Vellanki, P., & Venkatesh, S. (2020). Bayesian optimization for adaptive experimental design: A review. IEEE access, 8, 13937-13948. Link * Brochu, E., Cora, V. M., & De Freitas, N. (2010). A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning. arXiv preprint arXiv:1012.2599. Link

Gaussian Processes

Williams, C. K., & Rasmussen, C. E. (2006). Gaussian processes for machine learning (Vol. 2, No. 3, p. 4). Cambridge, MA: MIT press. Link * Leibfried, F., Dutordoir, V., John, S. T., & Durrande, N. (2020). A tutorial on sparse Gaussian processes and variational inference. arXiv preprint arXiv:2012.13962. Link

Acquisition functions and their optimization

Močkus, J. (1975). On Bayesian methods for seeking the extremum. In Optimization techniques IFIP technical conference (pp. 400-404). Springer, Berlin, Heidelberg. * Srinivas, N., Krause, A., Kakade, S. M., & Seeger, M. (2009). Gaussian process optimization in the bandit setting: No regret and experimental design. arXiv preprint arXiv:0912.3995. * Frazier, P., Powell, W., & Dayanik, S. (2009). The knowledge-gradient policy for correlated normal beliefs. INFORMS journal on Computing, 21(4), 599-613. * Hennig, P., & Schuler, C. J. Entropy search for information-efficient global optimization. Journal of Machine Learning Research (JMLR), 13, 1809–1837, 2012. * Hernandez-Lobato, J. M., Hoffman, M. W., & Ghahramani, Z. Predictive entropy search for efficient global optimization of black-box functions. Advances in Neural Information Processing Systems (NIPS), pp. 918–926, 2014.