【ICML2023】路径神经网络:具有表达能力的准确图神经网络

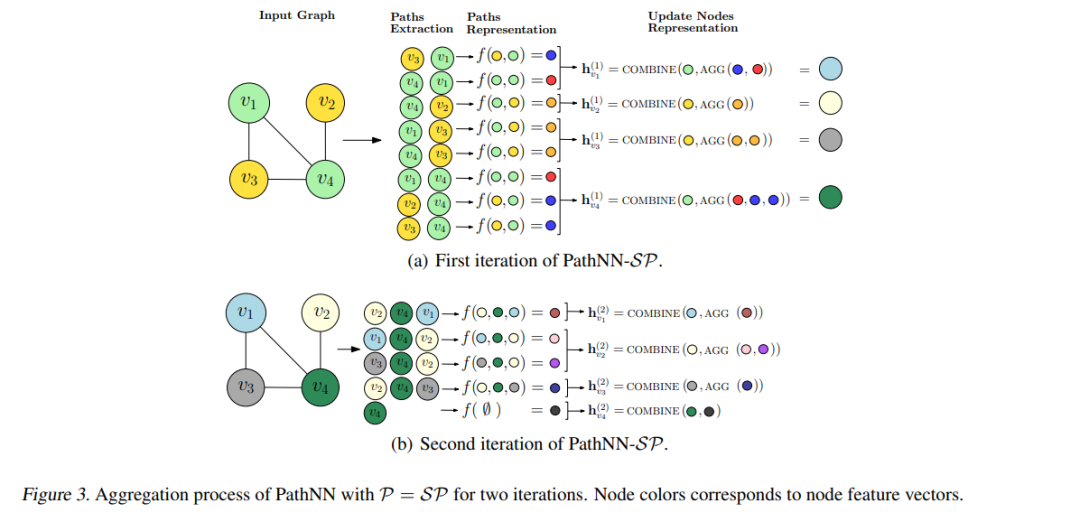
近期，图神经网络（GNNs）已成为处理图结构数据的标准方法。先前的研究揭示了它们的潜力，但也指出了它们的局限性。不幸的是，已经有研究表明标准的 GNNs 在表达能力上存在限制。这些模型在区分非同构图方面的能力并不超过一维 Weisfeiler-Leman（1-WL）算法。在本文中，我们提出了路径神经网络（PathNNs），这是一种通过聚合从节点发出的路径来更新节点表示的模型。我们推导出 PathNN 模型的三种不同变体，它们分别聚合单个最短路径、所有最短路径以及长度最多为 K 的所有简单路径。我们证明其中的两种变体在表达能力上严格超过了 1-WL 算法，并且我们通过实验验证了我们的理论结果。我们发现 PathNNs 能够区分那些 1-WL 无法区分的非同构图对，而我们最具表达能力的 PathNN 变体甚至可以区分 3-WL 无法区分的图。我们还在图分类和图回归数据集上评估了不同的 PathNN 变体，在大多数情况下，它们的性能优于基线方法。