「机器学习最优传输」最新进展, 巴黎萨克雷大学编著

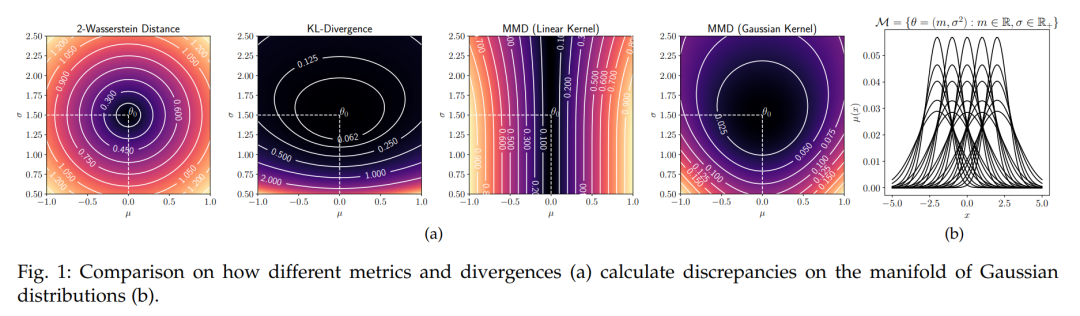
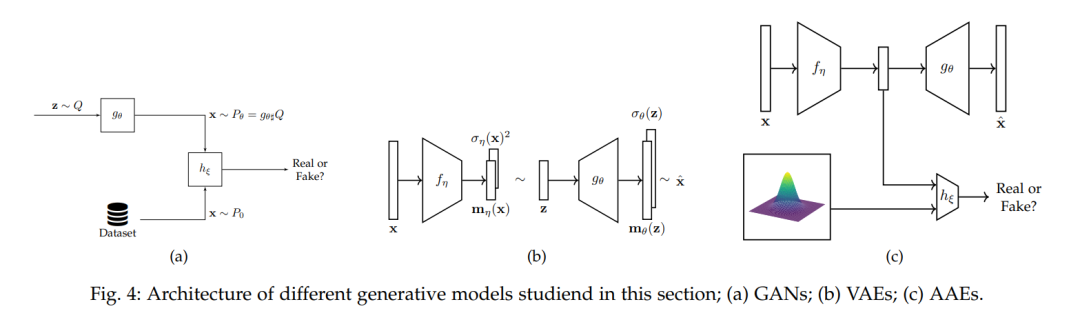
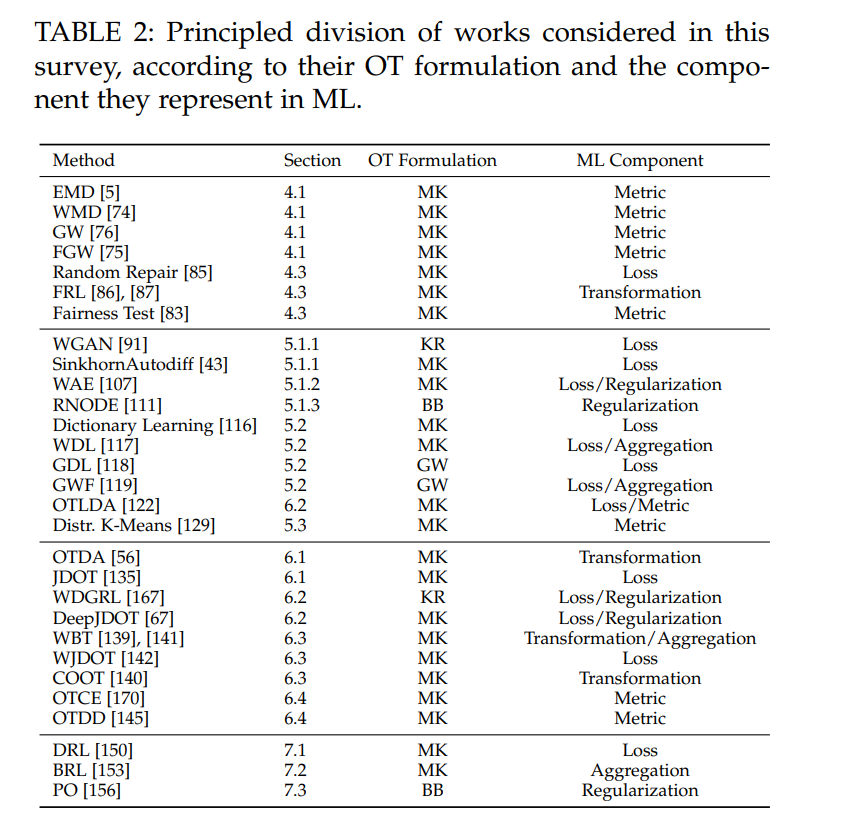
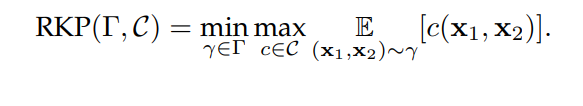最近，最优传输被提出作为机器学习中用于比较和操纵概率分布的概率框架。这植根于其丰富的历史和理论，并为机器学习中的不同问题提供了新的解决方案，如生成建模和迁移学习。在这篇综述中，我们探讨了2012年至2022年期间最优传输在机器学习方面的贡献，重点关注机器学习的四个子领域：监督学习，无监督学习，迁移学习和强化学习。我们进一步强调了计算最优传输的最近发展，以及它与机器学习实践之间的相互作用。

最优传输理论是一个由Gaspard Monge [1]和经济学家Leonid Kantorovich [2]的工作奠基的数学领域。自从它的诞生以来，这一理论在数学[3]，物理学[4]和计算机科学[5]方面做出了重大贡献。在这里，我们研究最优传输（OT）是如何为机器学习（ML）中的不同问题做出贡献的。机器学习的最优传输（OTML）是ML社区中一个不断发展的研究课题。实际上，OT至少从两个角度对ML有用：（i）作为损失函数，（ii）用于操纵概率分布。首先，OT定义了分布之间的度量，以不同的名字为人们所熟知，如Wasserstein距离，Dudley度量，Kantorovich度量或者Earth Mover Distance（EMD）。此度量属于积分概率度量（IPMs）的家族（参见2.1.1节）。在许多问题中（如生成建模），由于其拓扑和统计特性，Wasserstein距离比其他分布差异的概念（如Kullback-Leibler（KL）散度）更为可取。其次，OT本身就是一个工具包或框架，供ML从业者操纵概率分布。例如，研究人员可以使用OT通过Wasserstein重心和测地线聚合或插值概率分布。因此，OT是研究概率分布空间的一种原则性方法。本调查提供了近年来OTML的最新视角。尽管之前存在调查[6]-[11]，但该领域的快速发展证明了对OTML进行更仔细审查的必要性。本文的其余部分按以下方式组织。第2节讨论ML的不同领域的基础知识，以及OT的概述。第3节回顾了计算最优传输的最近发展。进一步的章节探讨OT在4个ML问题上的应用：监督学习（第4节），无监督学习（第5节），迁移学习（第6节）和强化学习（第7节）。第8节以总结和未来研究方向结束本文。

在介绍OT在ML方面的最新贡献之前，我们简要回顾了与相关主题有关的先前综述。关于OT作为数学领域，有大量的文献可供参考。例如，[12]和[13]从连续的角度介绍OT理论。该领域最完整的文本仍然是[3]，但它远非入门文本。正如我们在本调查中介绍的，OT为ML做出的贡献在本质上是计算性的。在这个意义上，从业者将专注于离散公式和如何实施OT的计算方面。这是[9]和[10]这两篇调查的情况。虽然[9]作为OT及其离散公式的介绍，[10]则提供了更广泛的视角，介绍了OT的计算方法以及它如何广泛应用于数据科学。在OT为ML方面，我们将我们的工作与[7]和[11]进行比较。前者介绍了OT的理论，并简要讨论了OT在信号处理和ML（如图像去噪）中的应用。后者提供了OT为ML贡献的广泛领域的概述，按数据的结构分类（即，直方图，经验分布，图表）。

由于我们工作的性质，先前的OTML调查中处理的主题与我们的主题之间存在一定程度的交集。每当出现这种情况时，我们提供有关主题的最新视角。我们强调一些新的主题。在第3节中，投影稳健、结构化、神经和小批量OT是计算OT的新方法。在8.1节中，我们进一步分析了从有限样本估算OT的统计挑战。在第4节，我们讨论了OT在结构化数据和公平性方面的最新进展。在第5节，我们讨论Wasserstein自编码器和归一化流。此外，OT用于字典学习的介绍以及其在图数据和自然语言处理的应用也是新的。在第6节，我们介绍领域适应，并讨论标准领域适应设置的泛化（即，当有多个来源可用时）和可转移性。最后，在第7节，我们讨论分布式和贝叶斯强化学习以及策略优化。据我们所知，在先前的相关评论中没有涉及强化学习（RL）。

目录内容：

2. 背景知识

3 计算最优传输计算最优传输（Computational OT）是一个活跃的研究领域，在过去十年里取得了显著的发展。这一趋势通过出版物 [9]，[39] 和 [10] 以及像 [40] 和 [41] 这样的软件得以体现。这些资源为最优传输在机器学习（ML）及相关领域的最近普及奠定了基础。在计算最优传输中，主要有三种策略；(i) 离散化环境空间；(ii) 通过样本近似分布P和Q；(iii) 为P或Q假设一个参数模型。前两种策略使用Dirac delta函数的混合来近似分布。

4 监督学习在接下来的部分，我们讨论监督学习中的最优传输（参见2.2.1节了解基本定义）。我们将讨论分为：(i) OT作为样本之间的度量；(ii) OT作为损失函数；(iii) OT作为公平性的度量或损失。在本节中，我们回顾了OT在监督学习中的应用（参见2.2.1节了解此设置的基本定义）。我们将应用分为两类，(i) 作为度量使用OT和(ii) 作为损失使用OT，这对应于以下两个部分。

5 无监督学习在本节中，我们讨论利用Wasserstein距离作为损失函数的无监督学习技术。我们考虑三种情况：生成建模（第5.1节），表示学习（第5.2节）和聚类（第5.3节）。

6 迁移学习如2.2.3节中讨论的，当数据遵循不同的概率分布时，迁移学习（TL）是机器学习的一个框架。分布偏移的最一般情况对应于 PS(X, Y) ≠ PT(X, Y)。由于 P(X, Y) = P(X)P(Y|X) = P(Y)P(X|Y)，可能会发生三种类型的偏移[131]：(i) 协变量偏移，即 PS(X) ≠ PT(X)，(ii) 概念偏移，即 PS(Y|X) ≠ PT(Y|X) 或 PS(X|Y) ≠ PT(X|Y)，以及 (iii) 目标偏移，即 PS(Y) ≠ PT(Y)。本节的结构如下。在6.1和6.2节中，我们介绍OT如何在浅层和深层领域适应（DA）中使用。为了对该主题有更广泛的了解，包括其他基于OT的方法，可以参考深度领域适应的调查，如 [132] 和 [29]。在6.3节中，我们介绍OT如何为更一般的DA设置（例如，多源和异构DA）做出贡献。最后，6.4节涵盖了预测TL方法成功的方法。 7 强化学习在本节中，我们回顾了OT在强化学习（RL）中的三个贡献，分别是：(i) 分布式强化学习（DRL）（第7.1节），(ii) 贝叶斯强化学习（BRL）（第7.2节），以及 (iii) 策略优化（PO）（第7.3节）。强化学习基础的简要回顾在2.2.4节中提供。

8 结论和未来方向8.1 计算最优传输 在最近的计算最优传输（OT）文献中出现了一些趋势。首先，OT作为损失函数的使用越来越广泛（例如，[43]，[65]，[67]，[91]）。其次，mini-max优化出现在看似不相关的策略中，如SRW [52]，结构化OT [57]和基于ICNN的技术[61]。前两种情况包括提出新问题的工作，它们考虑了相对于基本成本的最坏情况。[160]通过一组凸的基本成本矩阵C提出了一个相对通用的框架。

8.2 监督学习最优传输（OT）在三个方面对监督学习做出贡献。首先，它可以作为一种度量方式用于比较对象。这可以整合到最近邻分类器或内核方法中，它具有定义丰富度量的优势[74]。然而，由于OT的时间复杂度，这种方法无法随着样本大小的增加而扩展。其次，Wasserstein距离可以用于定义标签间的语义感知度量[78]，[80]，这对分类很有用。第三，OT为公平性做出贡献，它试图找到对受保护变量不敏感的分类器。因此，OT提出了三个贡献：(i) 定义数据的转换，以便在转换后的数据上训练的分类器满足公平性要求；(ii) 定义一个强制公平性的正则化项；(iii) 给定一个分类器，定义一个公平性测试。第一点在概念上接近OT对DA的贡献，因为两者都依赖于重心投影来生成新数据。

8.3 无监督学习生成建模。这个主题一直是最活跃的OTML主题之一。这得到了像[91]和[92]这样的影响性论文对于理解和训练GANs的作用的证明。然而，Wasserstein距离是有代价的：在原始形式中计算负担繁重，并且在其对偶形式中具有复杂的约束。这种计算负担导致OT的早期应用考虑采用对偶形式，留下了如何执行Lipschitz约束的问题。在这方面，[92]、[93]提出了正则化器，间接执行此约束。此外，最近的实验证明和理论讨论表明，WGANs并没有估算Wasserstein距离[94]-[96]。与GANs相反，OT对自动编码器的贡献围绕原始公式，替代了普通算法中的对数似然项。在实践中，使用Wc部分解决了VAEs中的模糊问题。此外，[107]的工作起到了在VAEs[26]和AAEs[106]之间架桥的作用。此外，动态OT通过BB公式有助于CNFs。在这种情况下，一系列论文[111]，[166]已经表明，OT强制执行流量规律，从而避免了相关ODEs中的刚性。因此，这些策略提高了培训时间。字典学习。OT通过定义直方图之间的有意义度量[116]以及如何在概率空间中计算平均值[117]来为这个主题做出贡献，例子包括[118]和[119]。未来的贡献可以分析字典原子在Wasserstein空间中的插值流形。聚类。OT通过将具有n个样本的经验分布近似为具有k个样本代表簇的另一个分布，为聚类提供了一个分布视图。此外，Wasserstein距离可用于在分布空间中执行K-均值。

8.4 迁移学习 在UDA中，OT（最优传输）已经在各种领域展示出了最先进的性能，例如图像分类[56]，情感分析[135]，故障诊断[30], [167]以及音频分类[141], [142]。此外，该领域的进步包括可以处理大规模数据集的方法和架构，例如 WDGRL [138] 和 DeepJDOT [67]。这有效地巩固了 OT 作为在不同领域之间传递知识的有效和有用的框架。此外，异构 DA（领域自适应）[140] 是一个新的、具有挑战性且相对未被探索的问题，OT 特别适合解决。此外，OT 为 DA 的理论发展做出了贡献。例如 [144] 以Wasserstein距离为基础，为不同的 |Rˆ PT (h) − Rˆ PS (h)| 提供了一个界限，类似于[22]。作者的结果强调了 OT 计划中类稀疏结构在 DA 成功中起着突出的作用。最后，OT 为分析异构数据集定义了丰富的工具箱，作为概率分布。例如，OTDD [145] 通过利用基本成本中的特征和标签定义了数据集之间的层次度量。这个领域的新兴主题包括在有很多来源的情况下的适应性（例如 [139], [142], [168]），以及当分布在不可比领域中受支持时（例如 [140]）。此外，DA 与其他机器学习问题相互关联，如生成建模（即，WGAN和WDGRL）和监督学习（即，[85]和[56]的工作）。

8.5 强化学习[150]的分布式RL（强化学习）框架重新引入了现代RL中的早期思想，比如以奖励的分布来制定一个智能体的目标。这被证明是成功的，因为作者的方法在各种游戏基准测试中超过了最先进的水平。此外，[169]进一步研究了这个框架是如何与基于多巴胺的RL相关的，这突显了这种制定的重要性。同样，[153]提出了一种用于传播价值函数不确定性的分布式方法。这里，值得强调的是，虽然[150]关注的是奖励函数的随机性，[153]研究的是价值函数的随机性。在这个意义上，作者提出了一种变体的Q学习，称为WQL，该方法利用Wasserstein质心来更新Q函数的分布。从实践的角度来看，WQL算法在理论上是有根据的，并且性能良好。进一步的研究可以关注[150]、[151]和[153]之间的共同点，通过建立一个共同的框架或者通过经验比较两种方法来实现。最后，[156]探讨了在分布空间中的梯度流作为策略优化。这种形式主义可以被理解为梯度下降的连续时间对应物。