逆向强化学习研究综述*

逆向强化学习 (inverse reinforcement learning, IRL) 也称为逆向最优控制 (inverse optimal control, IOC), 是 强化学习和模仿学习领域的一种重要研究方法, 该方法通过专家样本求解奖赏函数, 并根据所得奖赏函数求解最 优策略, 以达到模仿专家策略的目的. 近年来, 逆向强化学习在模仿学习领域取得了丰富的研究成果, 已广泛应用 于汽车导航、路径推荐和机器人最优控制等问题中. 首先介绍逆向强化学习理论基础, 然后从奖赏函数构建方式 出发, 讨论分析基于线性奖赏函数和非线性奖赏函数的逆向强化学习算法, 包括最大边际逆向强化学习算法、最 大熵逆向强化学习算法、最大熵深度逆向强化学习算法和生成对抗模仿学习等. 随后从逆向强化学习领域的前沿 研究方向进行综述, 比较和分析该领域代表性算法, 包括状态动作信息不完全逆向强化学习、多智能体逆向强化 学习、示范样本非最优逆向强化学习和指导逆向强化学习等. 最后总结分析当前存在的关键问题, 并从理论和应 用方面探讨未来的发展方向.

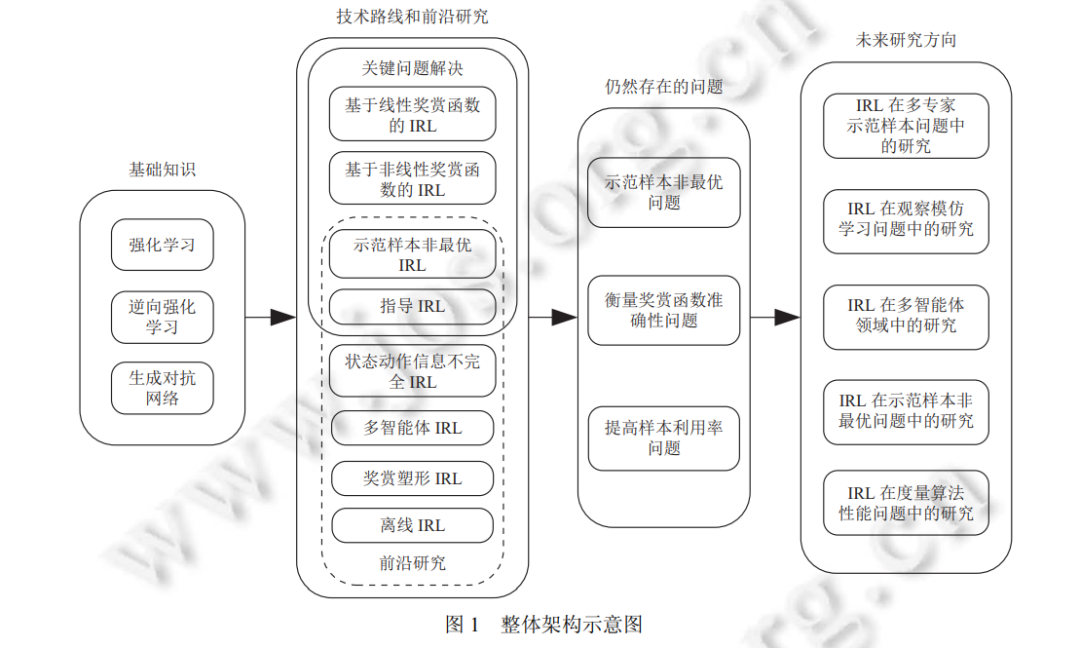
逆向强化学习 (inverse reinforcement learning, IRL) 作为一种学习专家策略的模仿学习算法, 已成功应用于汽 车导航[1]、路径规划[2,3]、行为预测[4−8]和机器最优控制[9−11]等领域. 近年来, 鉴于以上任务的复杂性和应用前景, 逆向强化学习已成为强化学习领域和模仿学习领域的研究热点. 本文旨在梳理逆向强化学习发展脉络, 介绍前沿 研究进展和分析关键问题. 逆向强化学习方法将模仿学习问题抽象为马尔可夫决策过程, 应用强化学习方法模仿专家策略. 与强化学习 依据奖赏函数求解最优策略不同, 逆向强化学习方法包含依据专家样本求解奖赏函数过程, 因其与强化学习方法 学习过程相反, 被称为逆向强化学习算法. 强化学习 (reinforcement learning, RL) 起源于最优控制领域, 是一种通过与环境交互求解最优策略的方法, 广 泛应用于工业制造[12]、机器人最优控制[13]、游戏博弈[14,15]、优化与调度[16−18]和仿真模拟[19]等领域. 强化学习方 法基于马尔可夫决策过程, 通过智能体与环境交互获得奖赏, 并根据累积奖赏更新策略以选取最优动作, 具有对环 境探索的自学能力. 算法在执行过程中持续探索环境和利用环境反馈信息, 使智能体的策略逐步迭代收敛至最优 策略.

此外, 强化学习方法中的奖赏函数由人工设定, 作为设计人员与智能体之间的沟通媒介, 奖赏函数中蕴含设 计人员所期望目标的全部信息, 而智能体通过与环境交互获得奖赏的方式“解码”奖赏函数, 完成期望任务. 模仿学习是一种通过专家样本模仿专家策略的方法[20,21] , 包括行为克隆方法 (behavioral cloning, BC) 和逆向 强化学习方法. 行为克隆[22,23]方法直接学习状态或标签到动作或路径的映射, 无需建立奖赏函数, 一般通过监督学习方法实 现. 对于小状态空间问题, 行为克隆是一种十分高效的方法. 但在连续状态-动作空间或大状态-动作空间问题中, 因为行为克隆方法只考虑在每个状态采取的动作与专家样本是否匹配, 不考虑未来收益, 所以若与环境交互路径 很长且专家样本不足, 则行为克隆方法会将细微误差在连续决策中逐步放大, 甚至环境发生一点变化, 都会极大影 响算法性能, 这被称为行为克隆方法中的复合误差问题[24,25] . 逆向强化学习也被称为逆向最优控制 (inverse optimal control, IOC)[26,27] , 最初由 Russell 于 1998 年提出[28] .

与强化学习方法相同, 逆向强化学习方法基于马尔可夫决策过程, 通过智能体与环境交互求解最优策略. 在一般强 化学习问题中, 奖赏函数由人工设定, 而在许多复杂问题中, 很难设计出精确的奖赏函数, 此时却很容易通过专家 策略采样专家样本, 例如汽车驾驶[29]和操纵机器打结等[30,31] . 针对这类问题, 逆向强化学习方法抛弃人工设定奖赏 函数过程, 直接通过专家样本重建奖赏函数, 并依据所得奖赏函数求解最优策略, 达到模仿专家策略的目的[32] . 相比行为克隆方法, 逆向强化学习方法具有更好的泛化性和鲁棒性[33,34] , 若环境改变或在专家样本状态-动作 空间之外, 仍可保证算法性能. 此外, 由于逆向强化学习方法通过最大化累积奖赏值求解最优策略, 所以逆向强化 学习方法方法不存在行为克隆方法中的复合误差问题. 逆向强化学习方法的奖赏函数最初为线性函数, 由 Ng 等人于 2000 年提出[35] , 此后基于学徒学习的逆向强化 学习算法[36]、最大边际算法[37]、最大熵算法[38]和相对熵算法[39]等被相继提出. 这类算法假设状态或状态-动作对 特征的线性组合为奖赏函数, 算法的最终目标为求解每个特征的系数, 当特征系数确定, 奖赏函数随之确定. 逆向 强化学习方法中多个奖赏函数均可求解专家策略, 这被称为非适定 (ill-posed) 问题, 算法仍需在满足条件的奖赏函数集合中选择最优解. Ng 等人基于启发式搜索思想要求奖赏函数满足约束条件的同时还需满足额外目标函数, 这一思想可用线性规划或二次规划数学模型表示.

因此, 早期逆向强化学习方法使用线性规划或二次规划方法求 解奖赏函数, 且奖赏函数为线性基函数, 依据不同目标函数, 基于基函数的算法分为 3 类: 基于最大边际思想的算 法、基于概率模型思想的算法和基于结构化分类思想的算法. 上述 3 类算法要求奖赏函数满足基本约束条件, 在 此基础之上, 基于最大边际思想的算法要求奖赏函数尽可能区分专家策略 (最优策略) 与次优策略, 即专家策略平 均回报尽可能大于次优策略平均回报. 基于概率模型思想的算法将问题抽象为概率模型, 每个奖赏函数对应的最 优路径 (trajectory) 都满足各自的概率分布[40] . 因此最大熵算法要求奖赏函数在满足基本约束条件的同时, 保证其 所对应最优路径概率分布的熵值最大, 类似还有基于交叉熵[41,42]、相对熵和最大似然估计[43]等算法. 基于结构化 分类思想的算法通过多个线性参数化分类器求解奖赏函数, 以使每个状态的累积回报尽可能大. 总体来说, 基于线 性奖赏函数的逆向强化学习算法在一些小状态空间和离散状态空间问题中取得了不错的效果, 且应用到汽车导航 问题中. 这类算法除相对熵算法外都是基于模型的算法, 因此需要提供环境模型 (状态转移概率), 在一定程度上限 制了算法的应用. 另外, 由于所有的奖赏函数都是特征的线性组合, 导致以下问题: (1) 特征需要凭借人的经验来选 取, 增加了算法的难度和不稳定性; (2) 线性奖赏函数形式简单, 存在表达能力有限的问题. 为克服线性奖赏函数的局限性, 基于非线性奖赏函数的逆向强化学习算法被提出, 包括基于贝叶斯的非参数 化特征构建算法[44]和基于神经网络的非线性逆向强化学习算法. 基于贝叶斯的非参数化特征构建算法用高斯过 程 (Gaussian processes, GPs)[45]构建非线性奖赏函数, 在一定程度上解决了线性奖赏函数表征能力不足的问题, 但 同时也需要提供大量专家样本. 传统逆向强化学习算法 (例如学徒学习算法、最大边际算法、最大熵算法、相对 熵算法) 与神经网络结合, 将神经网络作为奖赏函数, 取得了很好的效果. 这类算法可以通过神经网络自动提取状 态特征, 具有更强的表征能力. 目前, 在游戏、自动驾驶、路径导航和机器控制领域取得了一定成果. Ho 等人将在计算机视觉领域取得优秀成果的生成对抗网络 (generative adversarial network, GAN)[46]与逆向强 化学习结合, 提出生成对抗模仿学习算法 (generative adversarial imitation learning, GAIL)[47] . 该算法将逆向强化学 习过程抽象为求解奖赏函数的 IRL 过程和求解最优策略的 RL 过程, 并指出两个过程的交替迭代为零和博弈问题, 因此可用生成对抗思想解决. 相比非线性逆向强化学习算法, GAIL 具有更小的计算量和更高的性能, 但也存在训 练不稳定、模态崩塌 (mode collapse)[48]和生成样本利用率低的问题[49,50] . 近年来, 逆向强化学习方法在机器最优控制领域、状态动作信息不完全领域、多智能体领域和提高专家样本 利用率等领域都取得了进展, 也有学者将专家样本最优性假设进行扩展, 解决专家样本非最优问题[51−53] , 此外还有 指导逆向强化学习方法研究等[54−60] . 逆向强化学习方法发展至今, 已成为模仿学习方法中最重要的实现方式. 本文将基于以上分类, 梳理逆向强化 学习的发展脉络, 分析其发展的内部机理, 探讨其优势和不足, 并总结未来可能的发展方向. 本文的结构框架如后 文图 1 所示, 我们将按照图 1 结构, 介绍逆向强化学习领域的关键论文和最新进展.