![]() 当前动态系统呈现大型化、复杂化的趋势, 基于贝叶斯滤波的动态系统状态估计遇到一系列新的挑战. 随着深度学习在特征提取与模式识别等方面的优势与潜力不断显现, 深度学习与传统贝叶斯滤波相结合的研究也随之兴起. 为此, 梳理了不同领域融合深度学习的贝叶斯滤波方法的应用案例, 从中剖析不同类型动态系统下贝叶斯滤波存在的局限性和共性难题. 在此基础上, 总结了当前贝叶斯滤波存在的几类不确定性问题, 以深度学习的视角将这些问题归纳为特征提取和参数辨识两大基本问题, 进而介绍深度学习为贝叶斯滤波所提供的解决方案. 其次, 归纳整理了两类深度学习与贝叶斯滤波结合的具体方法, 着重介绍了深度卡尔曼滤波和融合深度学习的自适应卡尔曼滤波. 最后, 综合考虑深度学习方法和贝叶斯滤波方法的优势, 讨论了融合深度学习的贝叶斯滤波方法的开放问题和未来研究方向.
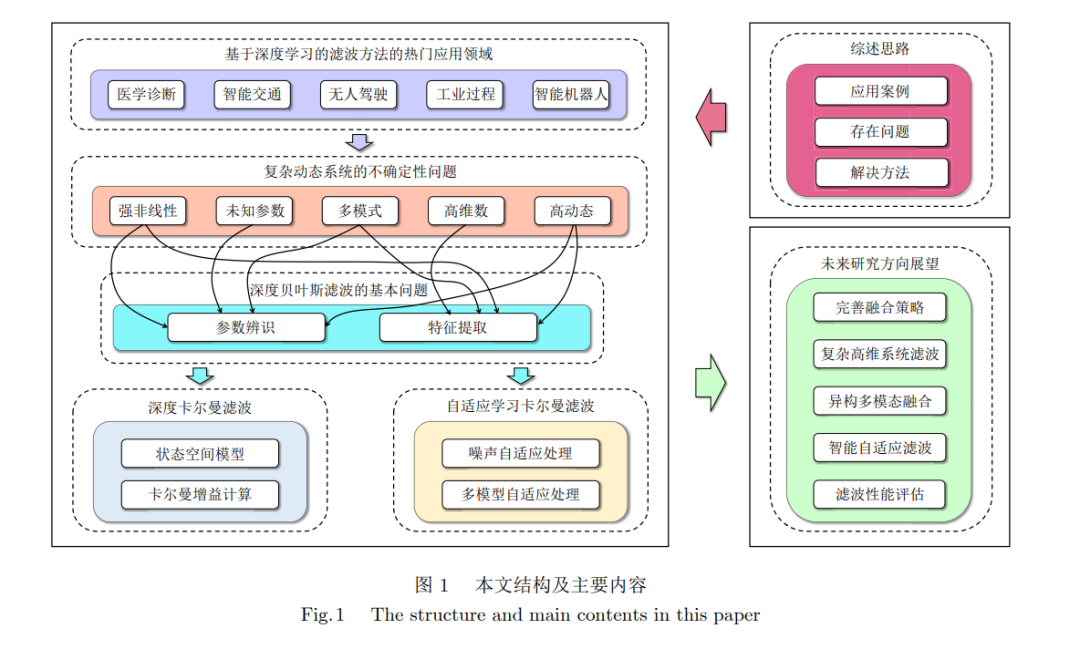
当前动态系统呈现大型化、复杂化的趋势, 基于贝叶斯滤波的动态系统状态估计遇到一系列新的挑战. 随着深度学习在特征提取与模式识别等方面的优势与潜力不断显现, 深度学习与传统贝叶斯滤波相结合的研究也随之兴起. 为此, 梳理了不同领域融合深度学习的贝叶斯滤波方法的应用案例, 从中剖析不同类型动态系统下贝叶斯滤波存在的局限性和共性难题. 在此基础上, 总结了当前贝叶斯滤波存在的几类不确定性问题, 以深度学习的视角将这些问题归纳为特征提取和参数辨识两大基本问题, 进而介绍深度学习为贝叶斯滤波所提供的解决方案. 其次, 归纳整理了两类深度学习与贝叶斯滤波结合的具体方法, 着重介绍了深度卡尔曼滤波和融合深度学习的自适应卡尔曼滤波. 最后, 综合考虑深度学习方法和贝叶斯滤波方法的优势, 讨论了融合深度学习的贝叶斯滤波方法的开放问题和未来研究方向. ![]() 随着信息技术的快速发展, 动态系统呈现大型 化、复杂化的新发展趋势, 系统观测数据呈现出多 模态、高维数、不确定性和多源异构等特性, 传统贝 叶斯滤波方法在处理这些观测数据时不断出现新的 困难和挑战, 如图像和激光点云数据. 另外, 由于动 态系统所具有的非线性、未知参数等特征, 加剧了 贝叶斯滤波方法在应用中的困难. 尤其是在实际场 景中, 复杂的外部环境干扰因素将导致动态系统存 在较强的不确定性, 从而增加传统滤波方法建立自 适应机制的难度. 近年来, 深度学习在图像处理[1–3]、语音识别[4–5] 和人机交互[6] 等领域上取得巨大的成功, 引起众多 学者对其理论和应用开展研究, 并利用深度学习方法 解决特定领域的一些问题, 如控制[7–8]、故障诊断[9–10]、 医学信息处理[11] 和导航定位[12] 等. 由于深度学习强 大的特征提取和高维数据处理能力, 人们也尝试将 深度学习方法与传统贝叶斯滤波方法相结合, 由此 形成了一种新的贝叶斯滤波方法体系, 即融合深度 学习的贝叶斯滤波. 卡尔曼滤波 (Kalman filtering, KF)[13] 是贝叶斯滤波在线性高斯系统上的表现形 式. 由于 KF 简洁的计算形式和良好的滤波性能, 越来越多的研究人员尝试将人工神经网络与之结 合, 尤其是深度神经网络 (Deep neural network, DNN), 如前馈神经网络 (Feedforward neural network, FNN)[14]、循环神经网络 (Recurrent neural network, RNN)[15] 和卷积神经网络 (Convolutional neural network, CNN)[16] 等. 早在 20 世纪 90 年代, Stubberud 等[17] 将一个 3 层 FNN 与扩展卡尔曼滤 波结合, 利用 FNN 来描述未建模动力学, 以提高滤 波精度. 之后, 卡尔曼滤波与 FNN 相结合的方法广 泛应用在各类任务中[18–19] , 进一步证实了该方法的 可行性和有效性. 随着新的深度神经网络技术的快 速发展, 融合深度学习的贝叶斯滤波得到进一步的 发展, 且应用领域也逐渐扩展到医学诊断[20–25]、智能 交通[26–31]、无人驾驶[32–36]、工业过程[37–40] 和智能机器 人[41–44] 等众多领域. 通过回顾不同领域中融合深度学习的滤波方 法, 可以发现, 该类方法正在开辟解决一些复杂问 题的新路径. 例如, 医学图像诊断领域呈现新的趋 势, 利用深度神经网络提取隐藏在图像中的病理特 征, 结合贝叶斯滤波进行病情推断; 智能交通领域, 开始寻求利用深度神经网络来处理交通大数据, 结 合贝叶斯滤波来调整交通决策; 无人驾驶领域, 正 在转向利用深度神经网络处理图像和激光雷达等观 测信息, 结合成熟的滤波框架搭建即时定位与地图 构建系统; 工业领域, 正在利用深度神经网络进行 工业大数据分析, 结合贝叶斯滤波挖掘数据的因果 关系; 智能机器人领域, 利用深度神经网络识别且 理解环境信息, 结合贝叶斯滤波进行状态推理和智 能决策已成为新趋势. 由于不同领域之间存在的差异性, 导致当前融 合深度学习的贝叶斯滤波方法研究进展的复杂性, 但是通过回顾融合深度学习的贝叶斯滤波的热门应 用, 对于典型滤波环境的转变与特点, 仍可以得出 一些基本结论: 动态系统的状态估计研究重心已从 早期简单的低维动态系统过渡到复杂的高维动态系 统, 从单智能体控制逐渐发展到多智能体协同控制, 从以机理为基础的建模方式发展到以深度神经网络 为基础的数据驱动学习方式, 从完美信息滤波逐渐 过渡到不完美信息滤波. 为此, 本文聚焦于贝叶斯 滤波, 结合信息融合理论的研究进展[45–46] , 从中总结 出一些当前动态系统滤波存在的关键问题. 本文的 思路将从实际应用案例出发, 挖掘其中存在的挑战 性问题, 并综述相关文献的解决方案和思路. 本文 的结构框架及主要内容如图 1 所示, 第 1 节概述贝 叶斯滤波方法, 结合当前复杂动态系统的新特点, 深入分析这些系统存在的滤波难点, 以此引出贝叶斯滤波方法面临的困难与挑战; 第 2 节归纳深度学 习在贝叶斯滤波中的作用, 包括参数辨识和特征提 取; 第 3 节详细介绍以卡尔曼滤波为基础的深度贝 叶斯滤波方法, 分析和总结当前国内外融合深度学 习的贝叶斯滤波方法的核心思想和解决方案, 以此 展示人工智能技术为滤波方法带来的新突破; 第 4 节阐述融合深度学习的自适应滤波方法; 第 5 节对 融合深度学习的贝叶斯滤波方法进行展望.
随着信息技术的快速发展, 动态系统呈现大型 化、复杂化的新发展趋势, 系统观测数据呈现出多 模态、高维数、不确定性和多源异构等特性, 传统贝 叶斯滤波方法在处理这些观测数据时不断出现新的 困难和挑战, 如图像和激光点云数据. 另外, 由于动 态系统所具有的非线性、未知参数等特征, 加剧了 贝叶斯滤波方法在应用中的困难. 尤其是在实际场 景中, 复杂的外部环境干扰因素将导致动态系统存 在较强的不确定性, 从而增加传统滤波方法建立自 适应机制的难度. 近年来, 深度学习在图像处理[1–3]、语音识别[4–5] 和人机交互[6] 等领域上取得巨大的成功, 引起众多 学者对其理论和应用开展研究, 并利用深度学习方法 解决特定领域的一些问题, 如控制[7–8]、故障诊断[9–10]、 医学信息处理[11] 和导航定位[12] 等. 由于深度学习强 大的特征提取和高维数据处理能力, 人们也尝试将 深度学习方法与传统贝叶斯滤波方法相结合, 由此 形成了一种新的贝叶斯滤波方法体系, 即融合深度 学习的贝叶斯滤波. 卡尔曼滤波 (Kalman filtering, KF)[13] 是贝叶斯滤波在线性高斯系统上的表现形 式. 由于 KF 简洁的计算形式和良好的滤波性能, 越来越多的研究人员尝试将人工神经网络与之结 合, 尤其是深度神经网络 (Deep neural network, DNN), 如前馈神经网络 (Feedforward neural network, FNN)[14]、循环神经网络 (Recurrent neural network, RNN)[15] 和卷积神经网络 (Convolutional neural network, CNN)[16] 等. 早在 20 世纪 90 年代, Stubberud 等[17] 将一个 3 层 FNN 与扩展卡尔曼滤 波结合, 利用 FNN 来描述未建模动力学, 以提高滤 波精度. 之后, 卡尔曼滤波与 FNN 相结合的方法广 泛应用在各类任务中[18–19] , 进一步证实了该方法的 可行性和有效性. 随着新的深度神经网络技术的快 速发展, 融合深度学习的贝叶斯滤波得到进一步的 发展, 且应用领域也逐渐扩展到医学诊断[20–25]、智能 交通[26–31]、无人驾驶[32–36]、工业过程[37–40] 和智能机器 人[41–44] 等众多领域. 通过回顾不同领域中融合深度学习的滤波方 法, 可以发现, 该类方法正在开辟解决一些复杂问 题的新路径. 例如, 医学图像诊断领域呈现新的趋 势, 利用深度神经网络提取隐藏在图像中的病理特 征, 结合贝叶斯滤波进行病情推断; 智能交通领域, 开始寻求利用深度神经网络来处理交通大数据, 结 合贝叶斯滤波来调整交通决策; 无人驾驶领域, 正 在转向利用深度神经网络处理图像和激光雷达等观 测信息, 结合成熟的滤波框架搭建即时定位与地图 构建系统; 工业领域, 正在利用深度神经网络进行 工业大数据分析, 结合贝叶斯滤波挖掘数据的因果 关系; 智能机器人领域, 利用深度神经网络识别且 理解环境信息, 结合贝叶斯滤波进行状态推理和智 能决策已成为新趋势. 由于不同领域之间存在的差异性, 导致当前融 合深度学习的贝叶斯滤波方法研究进展的复杂性, 但是通过回顾融合深度学习的贝叶斯滤波的热门应 用, 对于典型滤波环境的转变与特点, 仍可以得出 一些基本结论: 动态系统的状态估计研究重心已从 早期简单的低维动态系统过渡到复杂的高维动态系 统, 从单智能体控制逐渐发展到多智能体协同控制, 从以机理为基础的建模方式发展到以深度神经网络 为基础的数据驱动学习方式, 从完美信息滤波逐渐 过渡到不完美信息滤波. 为此, 本文聚焦于贝叶斯 滤波, 结合信息融合理论的研究进展[45–46] , 从中总结 出一些当前动态系统滤波存在的关键问题. 本文的 思路将从实际应用案例出发, 挖掘其中存在的挑战 性问题, 并综述相关文献的解决方案和思路. 本文 的结构框架及主要内容如图 1 所示, 第 1 节概述贝 叶斯滤波方法, 结合当前复杂动态系统的新特点, 深入分析这些系统存在的滤波难点, 以此引出贝叶斯滤波方法面临的困难与挑战; 第 2 节归纳深度学 习在贝叶斯滤波中的作用, 包括参数辨识和特征提 取; 第 3 节详细介绍以卡尔曼滤波为基础的深度贝 叶斯滤波方法, 分析和总结当前国内外融合深度学 习的贝叶斯滤波方法的核心思想和解决方案, 以此 展示人工智能技术为滤波方法带来的新突破; 第 4 节阐述融合深度学习的自适应滤波方法; 第 5 节对 融合深度学习的贝叶斯滤波方法进行展望.