《图神经网络不确定性》最新综述

图神经网络（GNNs）在各种实际应用中得到了广泛使用。然而，GNNs的预测不确定性来源于数据的固有随机性和模型训练错误等多种因素，这可能导致不稳定和错误的预测。因此，识别、量化和利用不确定性对于提高模型在下游任务的性能以及GNN预测的可靠性至关重要。本综述旨在从不确定性的视角提供对GNNs的全面概述，重点是其在图学习中的整合。我们比较和总结了现有的图不确定性理论和方法，以及相应的下游任务。因此，我们在理论和实践之间架起了桥梁，同时也连接了不同的GNN社区。此外，我们的工作为该领域中有前景的方向提供了宝贵的见解。

图神经网络（GNNs）已广泛应用于重要的实际应用中，包括异常检测[1]、分子属性预测[2]和交通规则化[3]。在这些领域内，GNNs对其预测不可避免地存在不确定性，导致不稳定和错误的预测结果。GNNs中的不确定性来源于多个方面，例如数据的固有随机性、GNN训练的错误、以及来自其他分布的未知测试数据。为了减轻预测不确定性对GNN预测的不利影响，系统地识别、量化和利用不确定性至关重要。在普遍的基于图的任务中，GNNs中的不确定性发挥着重要作用，例如在图主动学习[4]中选择标记的节点以及指示节点可能为分布外（OOD）的可能性[5]。此外，这种做法提高了GNNs的预测性能[6]，并加强了它们在决策制定中的可靠性，例如使GNNs对攻击具有鲁棒性[7]和解释哪些图的组件影响了GNN预测[8]。

为了通过不确定性提升GNNs，需要解决几个挑战。首先，需要识别GNNs中不同来源的不确定性，因为不确定性可能源自包括数据获取、GNN构建和推断[9]在内的多个阶段。其次，不同类型的不确定性应与相应的任务相匹配。例如，分布不确定性应用于图OOD检测[10]。第三，由于缺乏真实基准和统一的评估指标，正确量化GNNs中的不确定性很困难。最后，量化的不确定性可能需要适应并与其他组件结合以更好地服务于任务，例如图主动学习[11]。多项研究已努力解决这些挑战中的特定任务。在本文中，我们通过不确定性的视角提供这些任务的整体视图。

据我们所知，现有的综述或基准要么聚焦于更广泛的领域，即深度神经网络中的不确定性[12, 13, 9]和可信GNN[14]，要么聚焦于更狭窄的话题，例如时空GNNs中的不确定性[15, 16]。此外，这些综述主要讨论如何估计和测量不确定性，缺少关于如何将量化的不确定性应用于最终下游任务的具体和实际指导。我们的综述旨在通过从不确定性的视角对GNNs进行系统回顾来弥合这些差距，特别关注将不确定性整合进图学习。此外，我们的综述通过审查当前研究趋势来接近不确定性，尤其是跨不同下游任务的不同子社区，为更广泛的GNN社区做出贡献。我们的目标是提供一个全面的框架，澄清模糊的术语，连接几个社区，同时提供宝贵的见解和方向，以推进GNN不确定性及相关领域的整体发展。

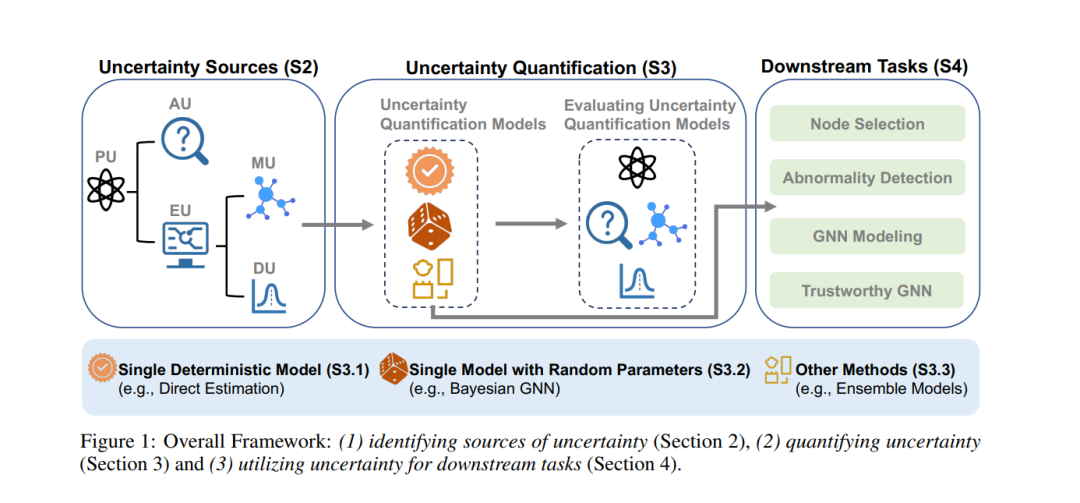
在本文中，我们将GNNs中的不确定性文献组织成一个三阶段框架，如图1所示。随后，在第5节中，我们介绍了利用GNN不确定性的实际应用。最后，在第6节中，我们讨论了这一领域未来研究的重要和有前景的途径。

量化GNNs中的不确定性

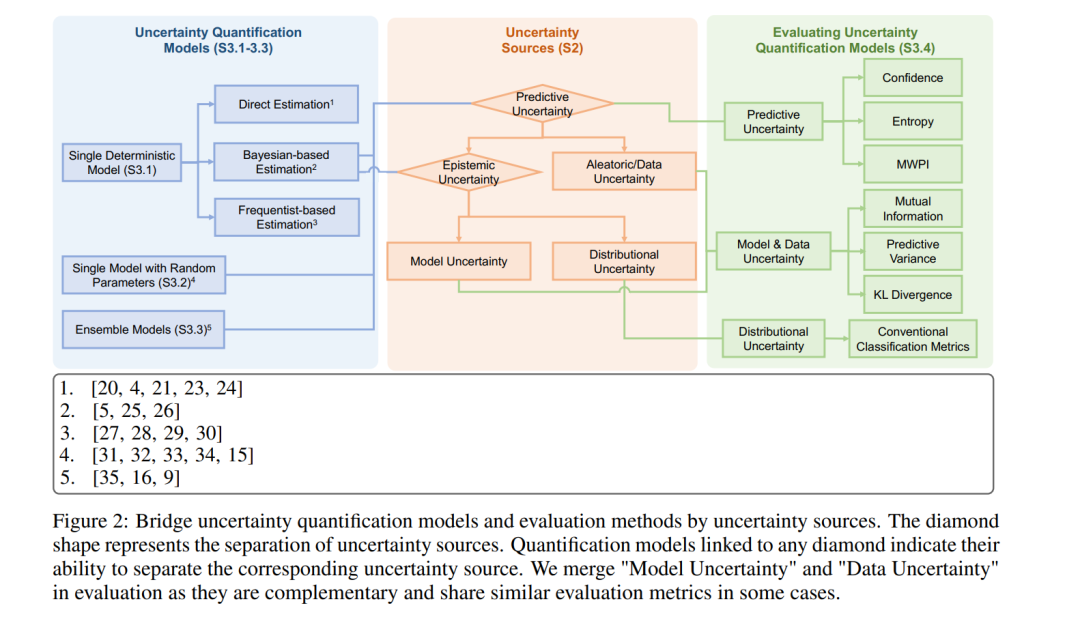
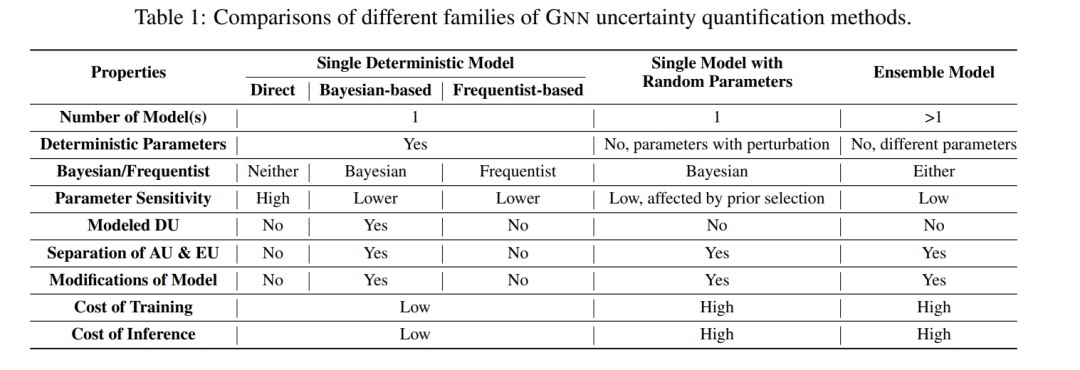
在本节中，我们根据模型的数量以及模型参数是随机的还是确定的，将现有的GNN不确定性量化方法分为三类，并随后介绍了这些方法的评估指标。在表1中，我们概述了各种量化方法的总结。 利用GNN任务中的不确定性

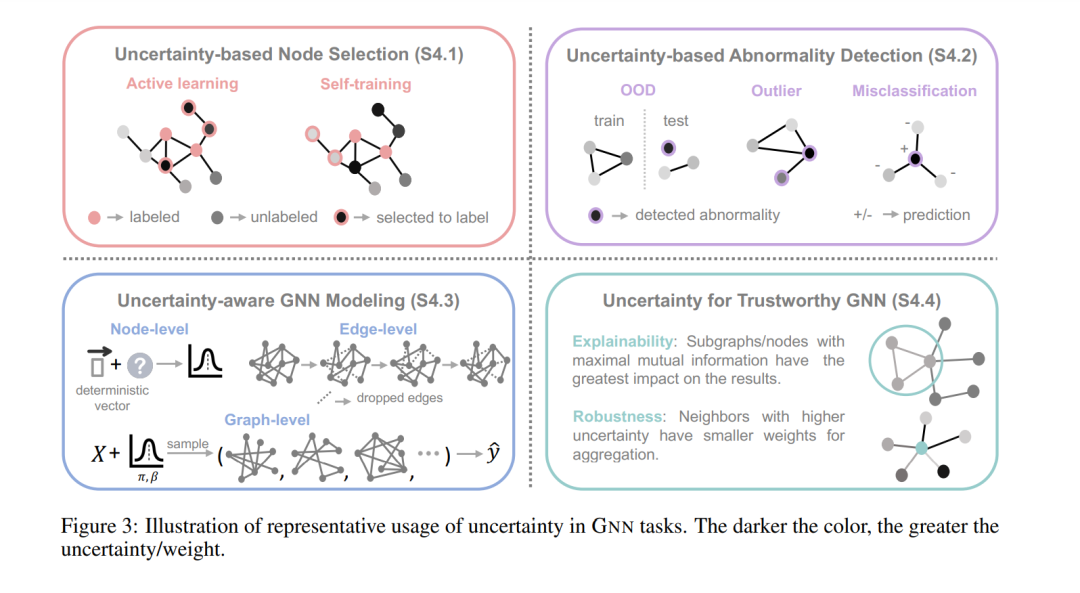
本节介绍了利用不确定性的四种类型GNN任务，如图3所述。除了确定不确定性的类型及其捕获方式外，我们还关注不确定性如何有助于任务目标。

应用

交通。GNNs被广泛用于建模网络交通，尤其是交通需求预测。交通系统中的不确定性在空间和时间上都会出现，例如，在体育场周围的比赛日，旅行需求可能会增加。[15]比较了六种不同的基于贝叶斯和频率主义的不确定性量化方法，用于道路网络交通预测问题，关于计算效率、渐进一致性等。[3]特别关注稀疏的旅行需求，并提出了STZINB-GNN，其中设计了一个带有额外稀疏参数的空间-时间嵌入，以学习输入为零的可能性。嵌入中的概率层允许以一定的信心级别进行预测，从而量化需求不确定性。[16]提出了一个概率GNN框架，Prob-GNN，来量化交通需求的时空不确定性。除了不同的GNNs，还比较了具有不同属性的不同概率分布假设，如拉普拉斯和高斯分布，以及单一和组合的高斯模型。Prob-GNN不仅能量化时空不确定性，而且在显著系统中断和识别异常大的不确定性下也能表现良好。实验结果表明，GNN性能更多受到概率分布假设的影响，而不是GNNs的选择，强调了将随机性和不确定性纳入交通预测模型的重要性。为了量化aleatoric和epistemic时空不确定性，[77]提出了DeepSTUQ，它使用贝叶斯dropout进行预训练，并使用集成方法进行再训练，然后使用温度缩放校准训练好的模型。在交通应用中，模型通常用点估计误差以及平均预测区间宽度(MPIW)来评估。

分子。药物发现是一个图级问题，旨在识别和开发具有期望属性的新分子，每个分子都被建模为一个图。[42]比较了不同的基于贝叶斯的方法，用于药物发现中准确和可靠的分子属性预测。他们揭示了几个关键方面：(1)epistemic和aleatoric不确定性都与错误相关，并提高了选择性预测的准确性，因此，应该利用总不确定性进行不确定性估计；(2)贝叶斯不确定性估计可以通过通知用户不确定性的级别来克服合成数据集的偏差；(3)估计的不确定性还应用于指导药物发现的主动学习，显示出具有最初多样化标记类的更好性能。类似地，[78]应用带有蒙特卡洛dropout的贝叶斯GNN来估计活性和毒性分类问题的不确定性。此外，他们使用aleatoric不确定性来评估现有和合成数据集的质量。为了减少药物发现中分布偏移下过度自信的误判，[79]引入了CardioTox，一个具有通过Tanimoto图距离注释的分子的新型实际OOD数据基准，并提出了一个距离感知分类器，GNNGP。后续研究[80, 81]也得出了类似的结论。在分子力场中，GNNs也表现出了促进分子动力学轨迹模拟的量子力学计算的有希望性能。除了对预测准确性、不确定性意识和计算成本的普遍关注外，[2]提出了物理信息的期望，包括对称性、能量守恒和局部性。除了评估先前的不确定性量化方法，他们提出了Localized SVGP-DKL，它结合了贝叶斯GNN和局部神经核，以满足与物理相关的标准。 其他。为了分割具有复杂几何或拓扑的图像，[82]使用GNNs来共同推理结构（节点）并捕获高阶空间相互作用（边）。概率模型提供了结构方面的不确定性估计，这可以识别出高度不确定的结构以供人工验证。在计算社会系统中，[83]应用一个不确定性感知的图编码器（UnGE）来表示职位标题为高斯嵌入，并捕获现实世界职业流动性中的不确定性。在故障诊断中，[84]提出了一个贝叶斯层次GNN，其中总不确定性通过dropout测量。使用不确定性作为权重，损失鼓励高度不确定样本的特征在时间上保持一致，以进行鲁棒特征学习。GNN中的不确定性也广泛应用于多个领域，包括能源[85]、机器人[86]和推荐系统[87]。