几何生成模型
·
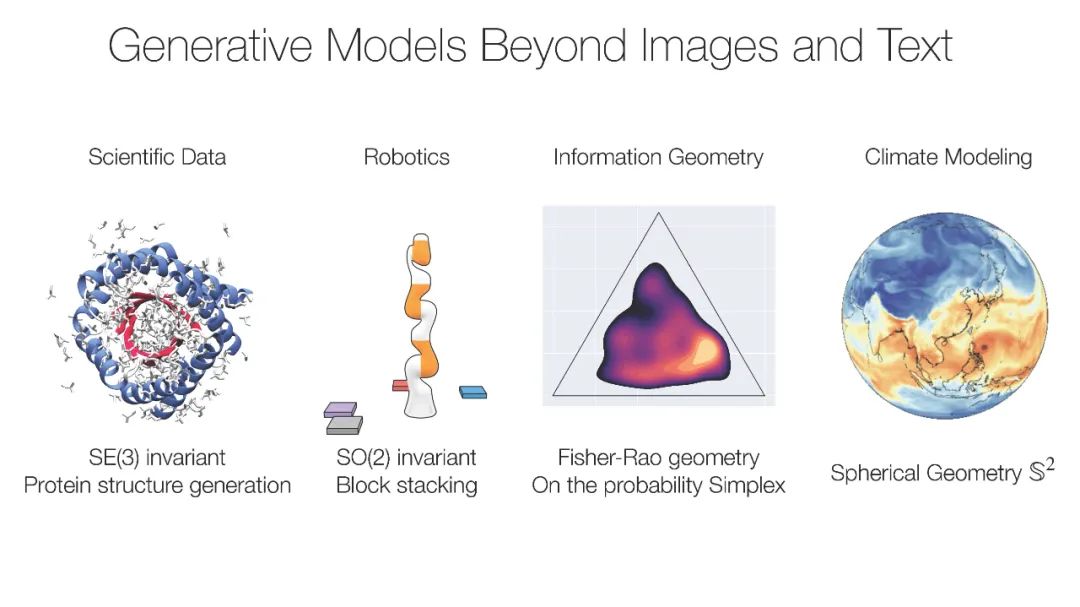
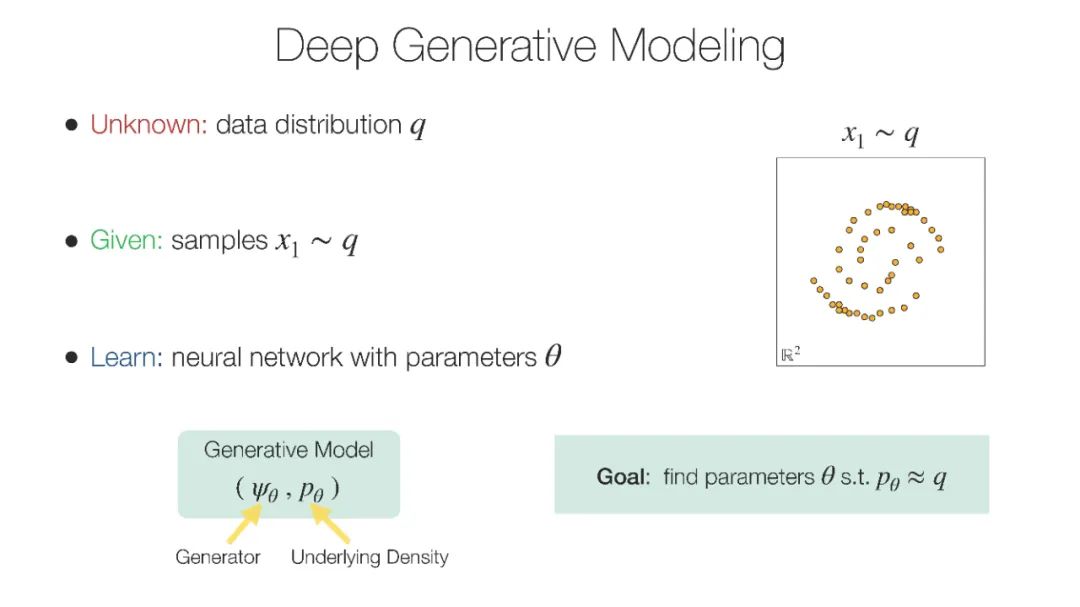
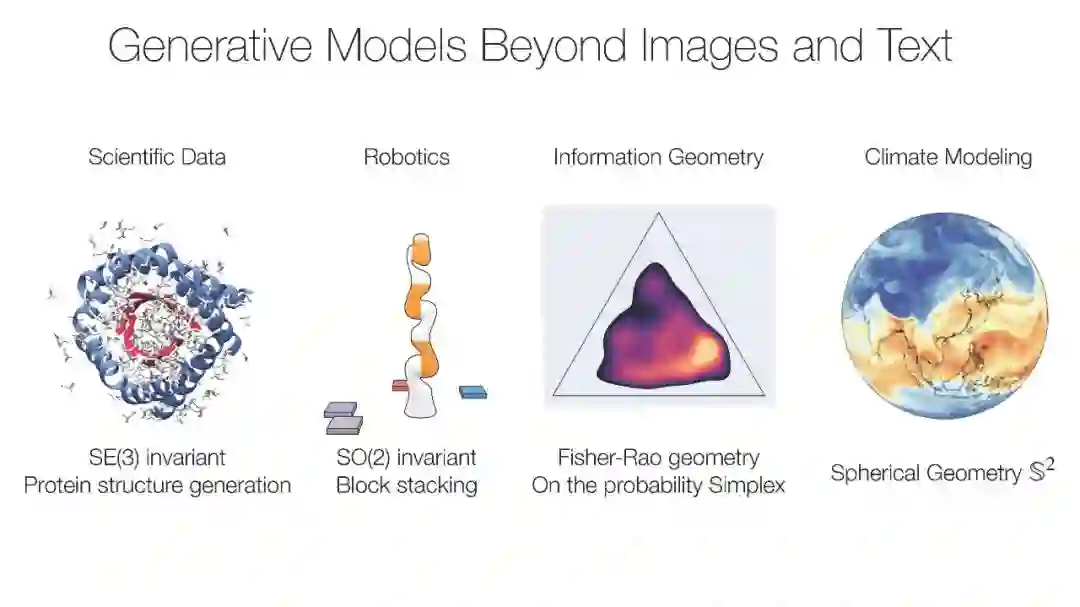
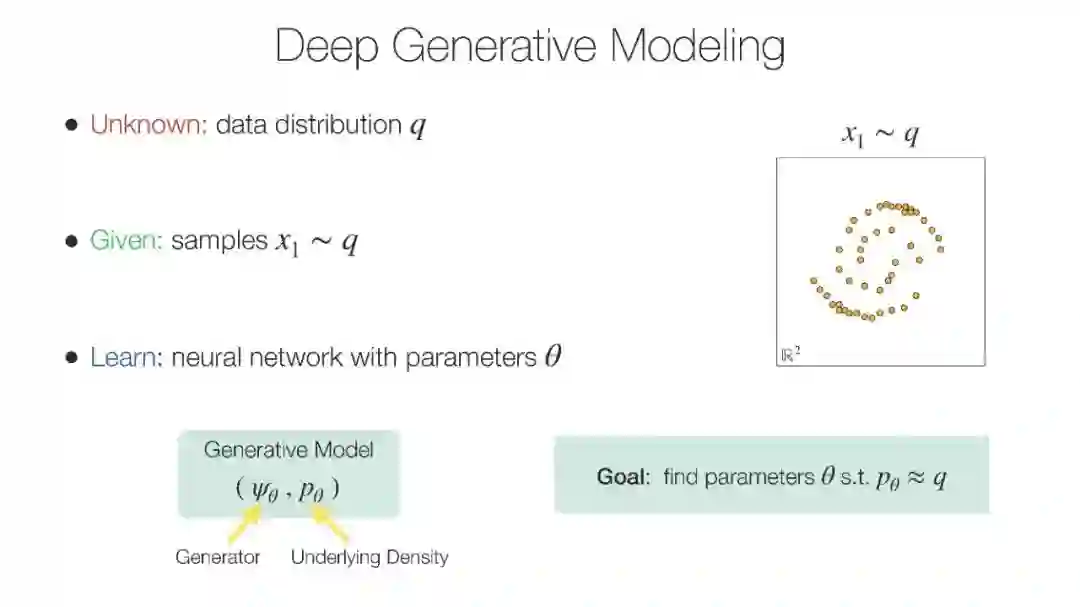
近年来,关于微分几何与生成建模在黎曼流形上的交集的研究呈现出激增趋势。事实上,许多高度结构化数据领域(例如表示分子数据和将地理空间数据视为球面上的点的图形)的应用增长,要求现代生成模型将数据的这一丰富结构视为不仅仅是可选的归纳偏差,而是作为驱动关键建模决策的一等公民。这引出了一个自然的问题:如何构建一个有原则的方法,将几何信息融入生成模型中。几何感知生成模型在这一领域中发挥着关键作用,并已在扩散和流匹配模型、蛋白质生成模型、机器人学以及动态系统对称性建模等重要应用领域产生了显著影响。目前,生成模型研究者与几何深度学习社区的交集相对较小,远不及各自母社区的规模。本教程旨在弥合这一差距,通过从底层视角讲解如何构建现代生成模型(如扩散模型和流匹配模型),并将其调适到那些从几何归纳偏差中受益的下游应用。我们的教程是首创之作,旨在为生成模型的新手以及经验丰富的几何机器学习专家提供几何蓝图,我们希望这能促进社区的壮大,并为新理论和应用的未来进展创造潜力。
https://sites.google.com/view/ggm-log-tutorial/home
成为VIP会员查看完整内容
相关内容
Arxiv
224+阅读 · 2023年4月7日