ECCV2022开会了！阿姆斯特丹大学122页《双曲表示学习计算机视觉》教程

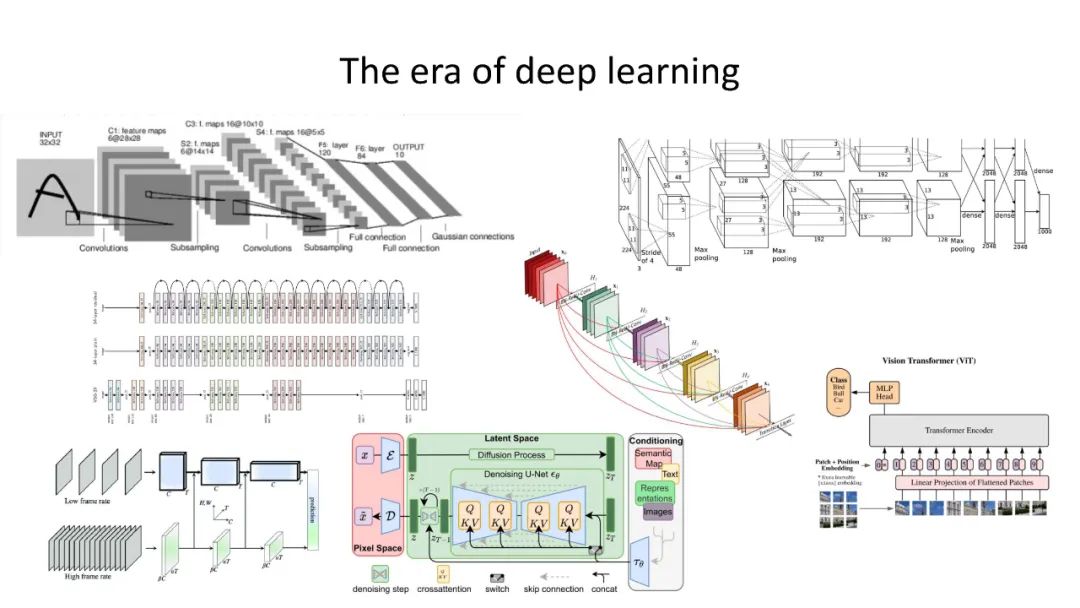
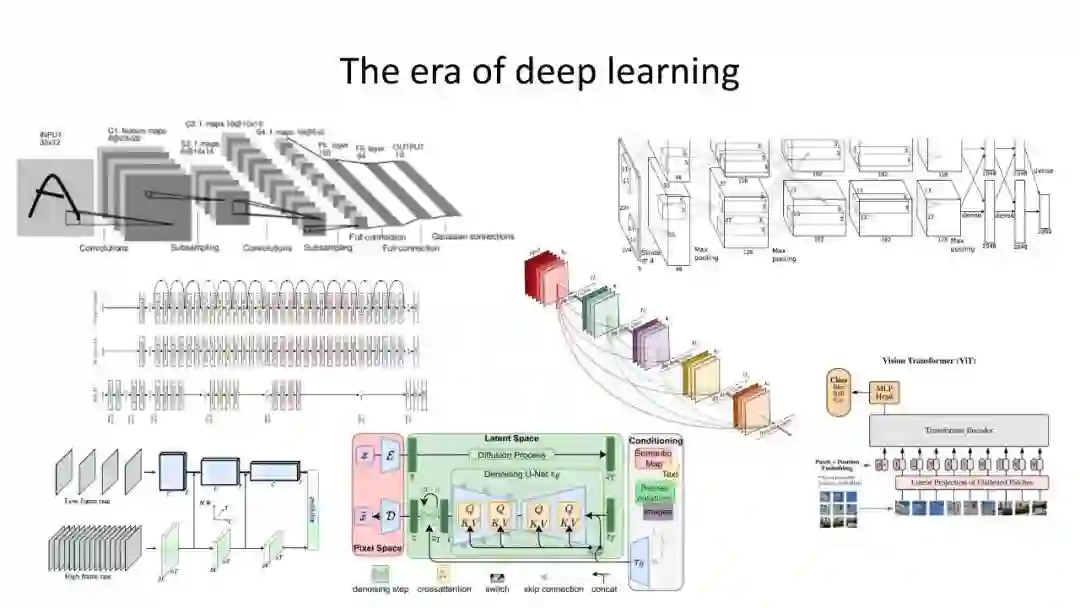
计算机视觉中的学习都是关于深度网络的，这种网络按设计在欧几里得流形上运行。但欧几里德几何是深度学习的最佳选择，还是仅仅是一个实用的选择?最近机器学习和计算机视觉方面的文献表明，双曲几何提供了一个强有力的替代方案，它可以改进嵌入层次结构、图表、文本、图像和视频的能力。 https://sites.google.com/view/hyperbolic-tutorial-eccv22/homepage?authuser=0

鉴于计算机视觉的双曲表示学习的最新进展，本教程试图向更广泛的受众宣传双曲几何及其在计算机视觉方面的强大潜力。本教程为该领域提供了一个理论和实践的起点。在会议上，我们将为非数学家提供一个简单的双曲几何介绍，在那里我们专注于直觉和高层次的理解。然后，我们从有监督和无监督的角度概述了视觉双曲几何的现状。最后，我们深入到开放的研究问题和双曲几何和视觉理解的未来潜力。 本教程的独特之处在于，我们没有停留在理论基础上。教程网站还将提供一系列笔记本风格的代码片段，其中包含双曲几何的基础工作，以便更好地理解其工作原理，降低障碍，开始深入研究计算机视觉这个令人兴奋的新研究方向。

9:00: Intro - Pascal Mettes 9.15: What is hyperbolic geometry? - Martin Keller-Ressel 10:15: Supervised hyperbolic learning - Mina GhadimiAtigh and Pascal Mettes 11:15: Unsupervised hyperbolic learning - Jeffrey Gu and Serena Yeung 12:00: Closing - Mina GhadimiAtigh and Pascal Mettes 讲者：