【IJCAI 2019】从可满足性到优化模理论（From Satisfiability to Optimization Modulo Theories），意大利特伦托大学副教授Roberto Sebastiani

报告主题： From Satisfiability to Optimization Modulo Theories

简介：

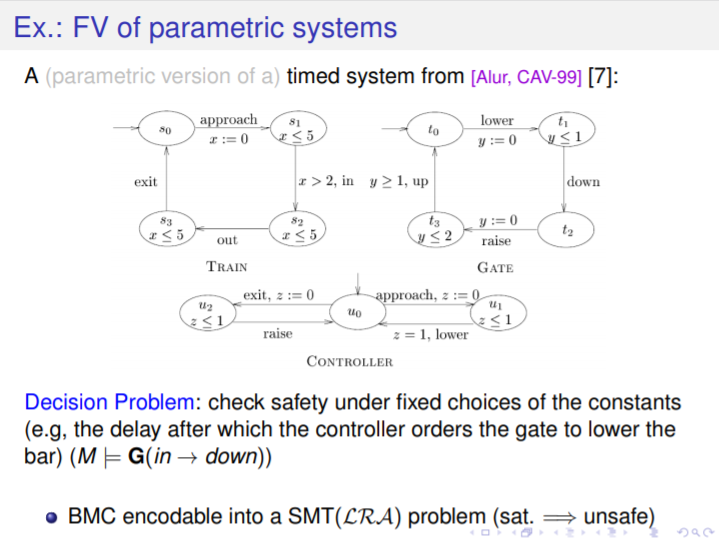
可满足性模理论(SMT)是决策的可满足性问题(通常quantifier-free)一阶公式对一些可决策的一阶理论(例如,rational LRA的线性运算或整数LIA及其数组AR,向量BV和浮点数的FP)及它们的组合。SMT引擎被广泛用作许多应用领域的后端引擎(包括规划、模型检查、需求工程、软件和HW验证)。然而，许多感兴趣的SMT问题都要求能够找到最优的wrt模型，一些目标函数。这些问题被归为优化模理论(OMT)一类。 本教程旨在提供OMT的主要问题、技术、功能和应用的概述，关注表达性和效率。具体的主题包括：支持在不同的兴趣理论中表达的目标函数;处理OMT增量;处理多个目标;处理重要的OMT子案例，如Max-SMT。我们简要地描述了一些有趣的应用。最后，指出了一些有待解决的问题和研究方向。

邀请嘉宾：

Roberto Sebastiani目前是意大利特伦托大学信息科学与工程系的副教授。他获得了意大利帕多瓦大学的电子工程硕士学位（1991年）和获得了意大利热那亚大学的计算机科学工程博士学位（1997年）。他目前的主要兴趣是优化模理论（OMT），可满足性模理论（SMT）及其在形式验证和AI问题中的应用。他的研究还涉及形式验证，SAT，模态和描述逻辑的决策程序，计划，定理证明。他发表了90多篇论文，其中许多论文发表在AI或与AI相关的期刊和会议上。