在这项工作中,我们解决了雷达波形优化和目标跟踪的问题。提出了一种基于控制论方法的优化波形设计和目标跟踪算法,其中波形参数是通过最小化跟踪均方误差(MSE)而自适应设计的。在这项工作中,采取了几种方法来提高雷达跟踪性能。首先,卡尔曼滤波器被用来估计目标位置,用它来优化波形参数。实验结果表明,所提出的算法有能力在笛卡尔空间内跟踪飞行目标,它提供了对目标位置和目标速度笛卡尔矢量以及径向速度的准确估计。该算法根据估计矢量在飞行中调整波形参数。在文献中,多普勒效应理论被大量用于估计目标速度。在某些条件下,如跟踪高速目标或恶劣的海洋和天气条件下,多普勒效应就不那么有效。因此,在这第一个方法中,引入了一种依赖于卡尔曼滤波估计的算法,而不依赖于多普勒效应。一个具有实时自适应参数的低通滤波器被应用于估计的速度矢量,并提取准确的速度估计。此外,从一个现实的角度来解决雷达跟踪问题,承认目标运动不能像我们提出的使用卡尔曼滤波器那样用矩阵来描述,因此引入了交互式多模型算法来估计目标位置。通过模拟,我们证明了所提算法的良好性能,并证明波形优化可以提高雷达的跟踪性能。最后,考虑从两个天线而不是一个天线收集信息,并使用其中一个数据融合算法,以及IMM算法,我们能够减少跟踪误差,并为跟踪问题提供一个更稳健可靠的解决方案。
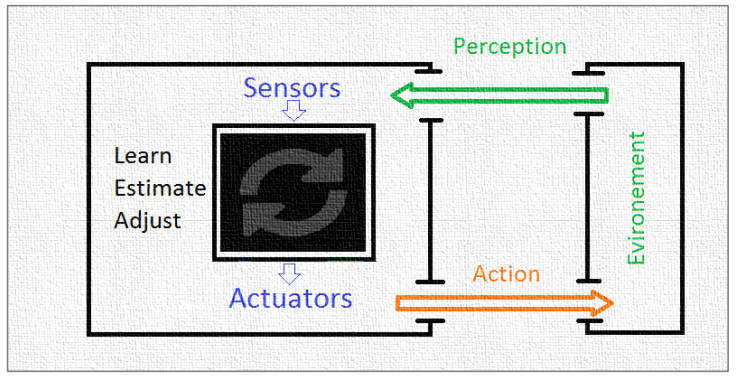
图 1. 大脑/认知雷达感知-行动周期。
认知被定义为参与认识、学习和理解事物的心理过程。这个定义介绍了定义CR的三个主要成分:
-
系统与环境持续互动并感知其地标的能力,包括潜在的目标和障碍物;这使得相控阵天线成为CR的主要组成部分,因为它们能够快速扫描环境。
-
智能地处理接收到的回波,并提取有关目标和周围环境的测量值的能力。
-
能够提取有关目标和环境的信息,并相应地使用它来做出有关波形和目标运动估计的决定。
认知型雷达在某种程度上模仿了大脑的学习方式,并根据感官采取行动,遵循一个类似的循环:感知、学习、调整、行动。它们不断地从环境中学习,并作出决定以提高跟踪性能。类似的循环,即众所周知的感知-行动循环(PAC),在解释大脑如何工作或描述一些智能系统的文献中被多次提及([2][3][4])。引用[2],神经科学家Joaquin Fuster将感知-行动循环描述为 "在处理目标导向行为的过程中,信息从环境到感觉结构,再到运动结构,再次回到环境,再到感觉结构,如此循环往复"。图1解释了与认知雷达相关的大脑的运行周期。在这项工作中,我们讨论了这个闭环循环的所有步骤,这些步骤制约着CR的性能。提出了一个系统模型,并进一步讨论了以估计和波形优化过程为重点的内容。
在文献中,讨论了两种主要的波形选择方法:控制论和信息论。在这项工作中,考虑了控制理论方法中的波形选择标准。雷达波形参数主要通过最小化跟踪均方误差(MSE)来确定。
CR有一个闭环的工作循环。该系统依靠接收器的反馈来收集关于目标和环境的知识。这些知识然后被用来优化发射波形,并改进对目标的探测、跟踪、估计和识别。这个概念在2006年由S.Haykin[1]在文献中首次提出,他写道,我们引用[1]"整个雷达系统构成了一个动态的封闭反馈回路,包括发射器、环境和接收器。
CR的运行周期(即上述闭环)从发射器对环境的照射开始。然后,从环境中反弹出来的传输波形(即目标回波、杂波等)被接收器截获。关于目标和环境的有用信息从接收到的回波中提取出来,然后更新一个信息库(记忆块),在下一个周期由目标估计器(TE)作为一组关于环境的先验知识使用。根据TE提供的估计结果,波形被优化。通常考虑用贝叶斯方法来实现目标估计器。
在CR中,提取的信息不仅在接收机层面发挥作用,而且在发射机层面通过改变波形和一些相关参数,如脉冲重复频率(PRF)、脉冲宽度、脉冲数N和雷达发射时间表来发挥作用。这方面是CR与经典的自适应雷达的区别,后者只能在接收层面使用提取的信息。
波形优化设计作为一个重要的研究课题出现在信号处理界,因为它在许多领域都有广泛的应用,如通信系统、声纳,以及在我们感兴趣的情况下,改善雷达系统的性能。文献中讨论了许多设计标准,其中我们提到了最大信噪比(SINR)标准[9]、最大探测概率标准[14]、最大互感信息(MI)[8]标准和最小化均方误差标准(MMSE)[10]、[11]。这些设计标准方法可以分为两类:控制理论方法,其目的是为连续运行的动态系统开发一个控制模型;信息理论方法,更侧重于研究信息流和从接收的测量数据中提取更多的目标信息。本文采用了控制理论方法,通过最小化跟踪MSE来确定最佳波形选择/设计。