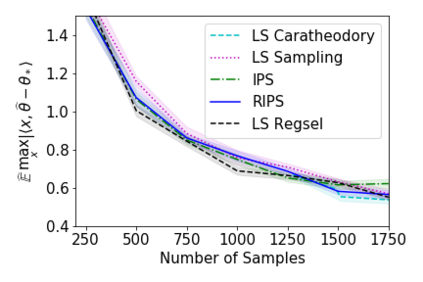
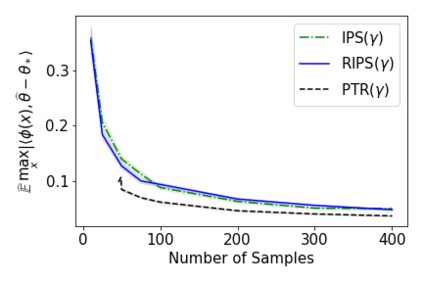
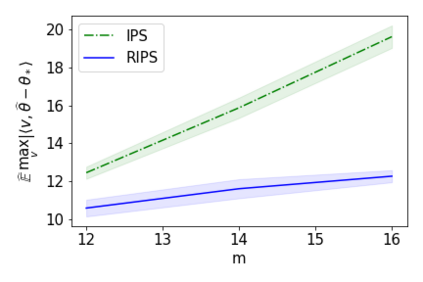
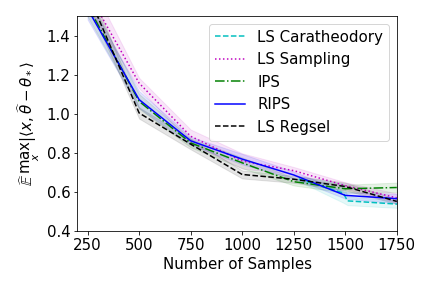
In recent years methods from optimal linear experimental design have been leveraged to obtain state of the art results for linear bandits. A design returned from an objective such as $G$-optimal design is actually a probability distribution over a pool of potential measurement vectors. Consequently, one nuisance of the approach is the task of converting this continuous probability distribution into a discrete assignment of $N$ measurements. While sophisticated rounding techniques have been proposed, in $d$ dimensions they require $N$ to be at least $d$, $d \log(\log(d))$, or $d^2$ based on the sub-optimality of the solution. In this paper we are interested in settings where $N$ may be much less than $d$, such as in experimental design in an RKHS where $d$ may be effectively infinite. In this work, we propose a rounding procedure that frees $N$ of any dependence on the dimension $d$, while achieving nearly the same performance guarantees of existing rounding procedures. We evaluate the procedure against a baseline that projects the problem to a lower dimensional space and performs rounding which requires $N$ to just be at least a notion of the effective dimension. We also leverage our new approach in a new algorithm for kernelized bandits to obtain state of the art results for regret minimization and pure exploration. An advantage of our approach over existing UCB-like approaches is that our kernel bandit algorithms are also robust to model misspecification.
翻译:近年来,从最佳线性实验设计中得出的最佳线性实验设计方法已被利用,以获得线性土匪的最新结果。从“$G$-最佳设计”等目标返回的设计实际上是潜在测量矢量集合的概率分布。因此,这一方法的一个麻烦之处是将这种连续的概率分布转换成独立的美元测量任务。虽然提出了复杂的四舍五入程序,用美元计算,它们至少需要美元、美元/log(d)美元或以解决方案的亚最佳度为基础的美元2美元。在本文件中,我们感兴趣的环境是,美元可能远远低于美元,例如,在RKHS的实验性设计中,美元可能实际上无限。在这项工作中,我们提议了一个四舍五入的程序,使美元对维度标准值的依赖度为美元,同时实现现有四舍五入程序的几乎相同的业绩保障。我们根据一个基线,将问题投射到更低维度的轨道空间,并进行更接近我们目前最精确的亚值的亚化方法。我们目前最起码的亚级的亚级方法要求我们获得一个比亚性强的亚级的亚值。