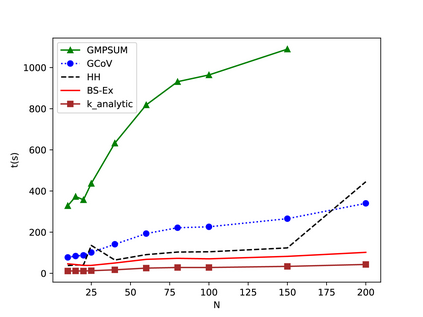
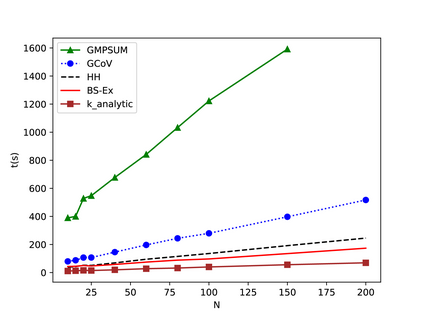
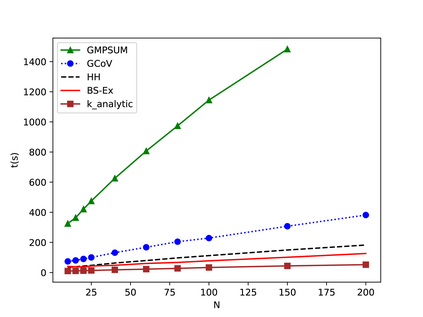
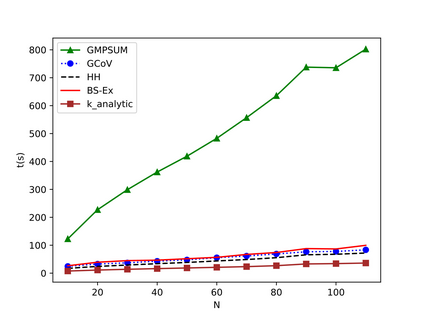
The Longest Common Subsequence Problem (LCS) deals with finding the longest subsequence among a given set of strings. The LCS problem is an NP-hard problem which makes it a target for lots of effort to find a better solution with heuristics methods. The baseline for most famous heuristics functions is a tabular random, probabilistic approach. This approach approximates the length of the LCS in each iteration. The combination of beam search and tabular probabilistic-based heuristics has led to a large number of proposals and achievements in algorithms for solving the LCS problem. In this work, we introduce a closed-form equation of the probabilistic table calculation for the first time. Moreover, we present other corresponding forms of the closed-form equation and prove all of them. The closed-form equation opens new ways for analysis and further approximations. Using the theorems and beam search, we propose an analytic method for estimating the length of the LCS of the remaining subsequence. Furthermore, we present another heuristic function based on the Coefficient of Variation. The results show that our proposed methods outperform the state-of-the-art methods on the LCS problem.
翻译:长期常见子序列问题( LCS) 涉及在给定的字符串中找到最长的子序列。 LCS 问题是一个NP- 硬问题, 使得它成为许多努力寻找更佳方法的方法的目标。 最著名的超光速函数的基准是一种表格随机、 概率性的方法。 这种方法在每次迭代中接近 LCS 的长度 。 梁搜索和表格概率性超常的结合导致在解决 LCS 问题的算法中有大量的建议和成就 。 在这项工作中, 我们首次采用了概率表计算方法的封闭式方程式等式。 此外, 我们提出了其他对应的封闭式方程式等式, 并证明了所有这些方程式。 闭式方程式为分析和进一步近似开辟了新的方法。 我们使用标语和相搜索, 提出了一种分析方法来估计 LCS 剩余子序列的长度。 此外, 我们提出了另一种基于 CS 节率方法的超常函数, 展示了我们所提议的结果 。