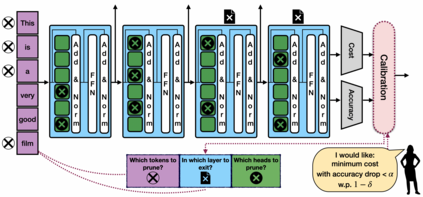
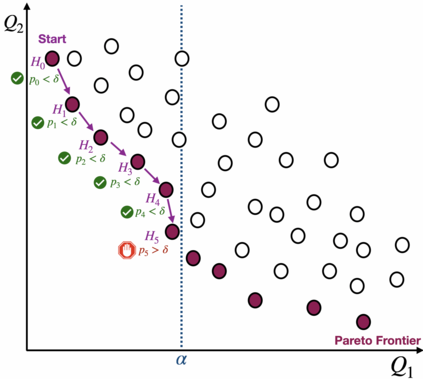
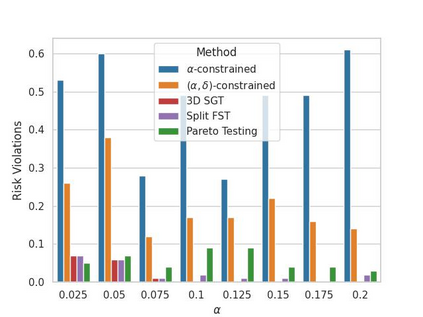
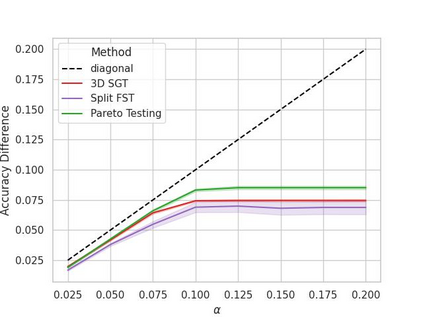
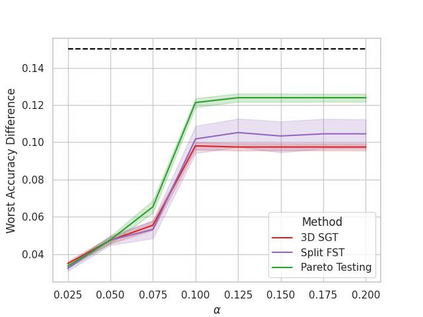
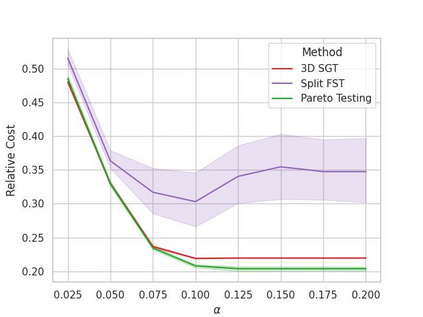
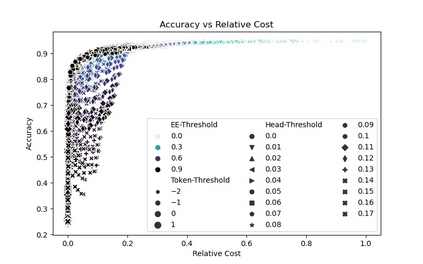
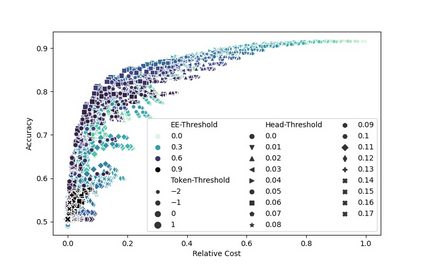
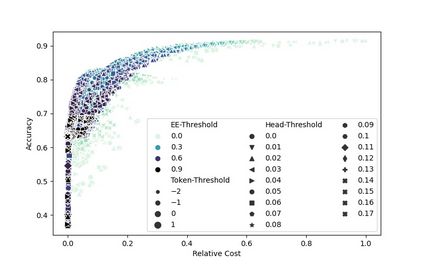
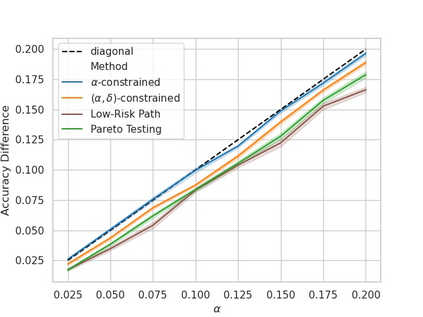
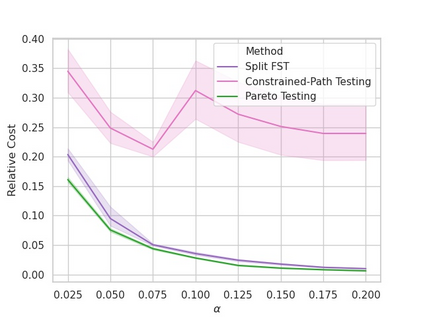
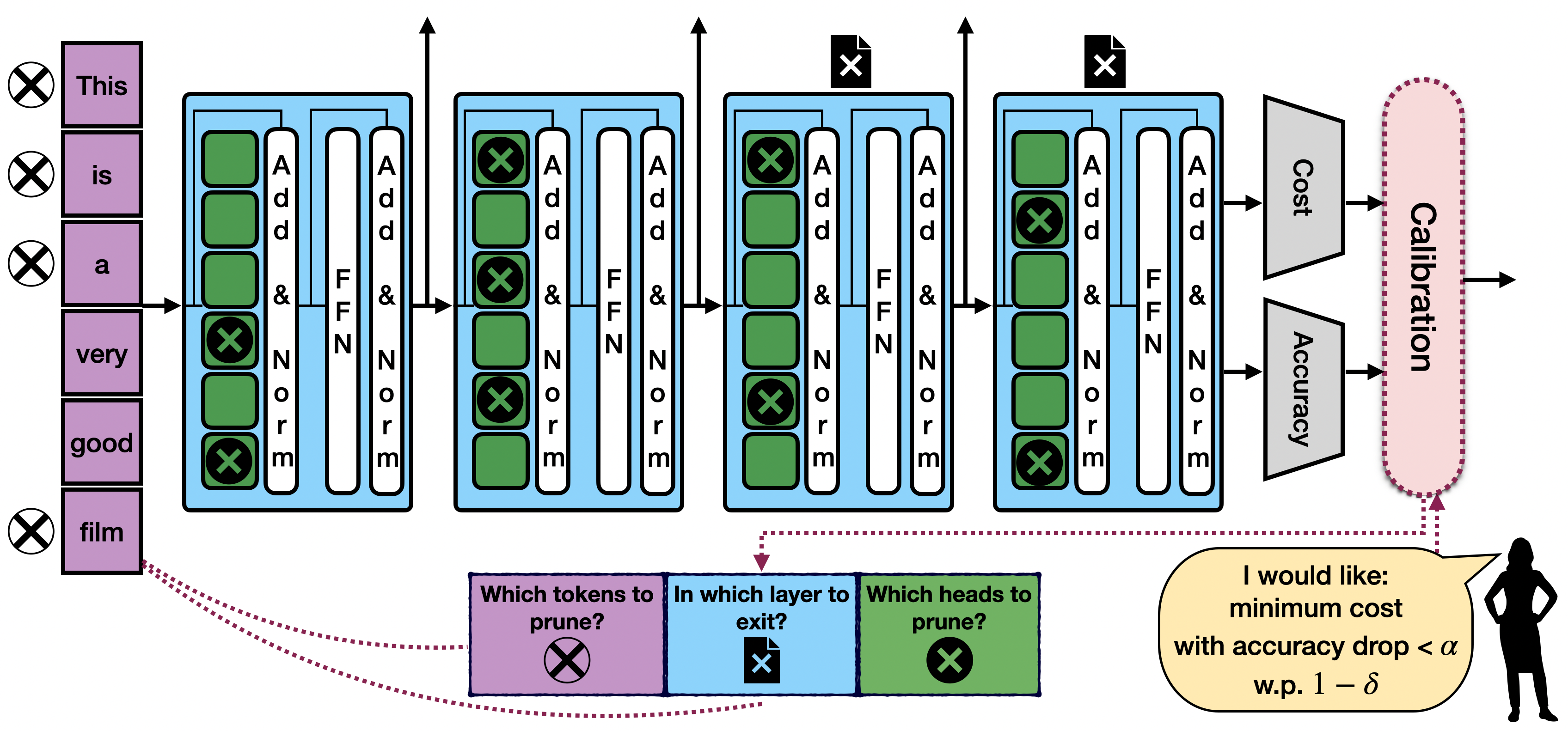
Machine learning applications frequently come with multiple diverse objectives and constraints that can change over time. Accordingly, trained models can be tuned with sets of hyper-parameters that affect their predictive behavior (e.g., their run-time efficiency versus error rate). As the number of constraints and hyper-parameter dimensions grow, naively selected settings may lead to sub-optimal and/or unreliable results. We develop an efficient method for calibrating models such that their predictions provably satisfy multiple explicit and simultaneous statistical guarantees (e.g., upper-bounded error rates), while also optimizing any number of additional, unconstrained objectives (e.g., total run-time cost). Building on recent results in distribution-free, finite-sample risk control for general losses, we propose Pareto Testing: a two-stage process which combines multi-objective optimization with multiple hypothesis testing. The optimization stage constructs a set of promising combinations on the Pareto frontier. We then apply statistical testing to this frontier only to identify configurations that have (i) high utility with respect to our objectives, and (ii) guaranteed risk levels with respect to our constraints, with specifiable high probability. We demonstrate the effectiveness of our approach to reliably accelerate the execution of large-scale Transformer models in natural language processing (NLP) applications. In particular, we show how Pareto Testing can be used to dynamically configure multiple inter-dependent model attributes -- including the number of layers computed before exiting, number of attention heads pruned, or number of text tokens considered -- to simultaneously control and optimize various accuracy and cost metrics.
翻译:机器学习应用经常出现多种不同的目标和限制,随着时间的推移可能会发生变化。因此,经过培训的模型可以与影响其预测行为的超参数组合(例如,其运行时间效率相对于误差率)调整。随着制约和超参数维度数量的增长,天真的选择的设置可能导致低于最佳和(或)不可靠的结果。我们开发了一种有效的校准模型的方法,以便它们的预测能够明显地满足多种明确和同时的统计保证(例如,上限误差率),同时优化任何数量的额外、不受限制的目标(例如,总运行时间成本),从而影响其预测行为(例如,运行时间效率相对于错误率)。随着限制和超参数维度维度的尺寸的增多,我们建议Pareto测试:一个将多目标优化与多重假设测试相结合的两阶段进程。优化阶段在Pareto边界模型上构建一套有希望的组合。我们随后对边界进行统计测试,只是为了确定一些被认为(i) 对我们的目标具有高度效用的不固定目标(例如,整个运行时间成本成本成本成本成本成本成本成本),以及(ii) 保证实施风险水平,以及(我们快速操作的升级的深度) 测试中所使用的大规模测试中,我们所使用的多种语言的深度, 显示我们所使用的大规模操作的概率,以及大规模操作,我们所使用的大规模操作的高度,我们所使用的各种语言的频率,可以显示我们使用。