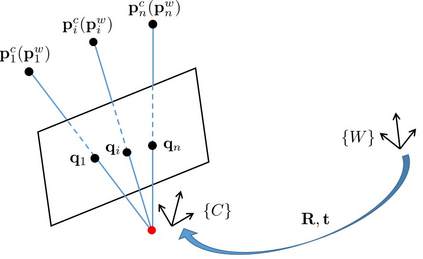
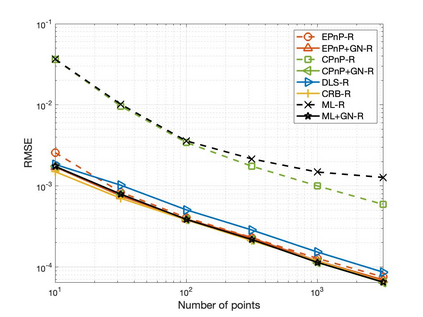
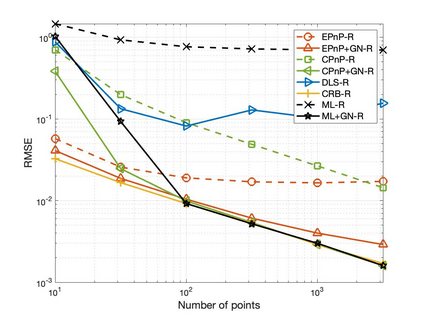
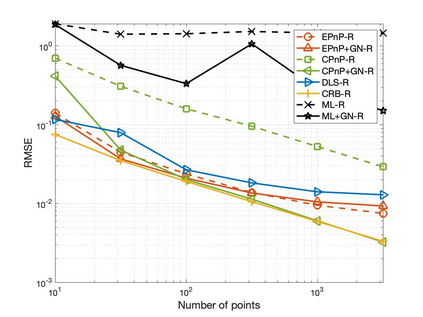
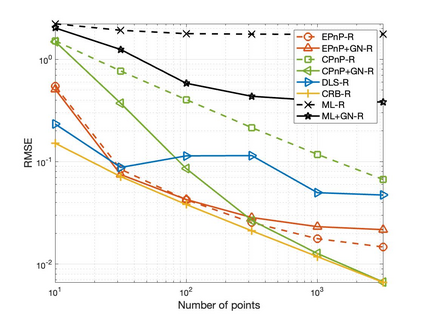
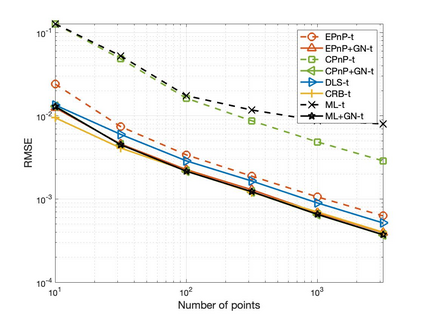
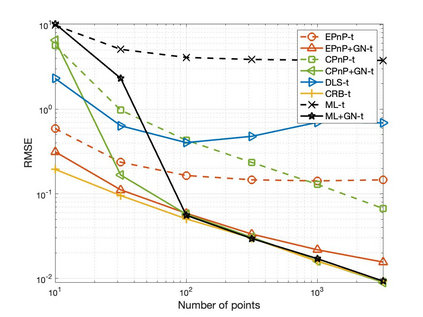
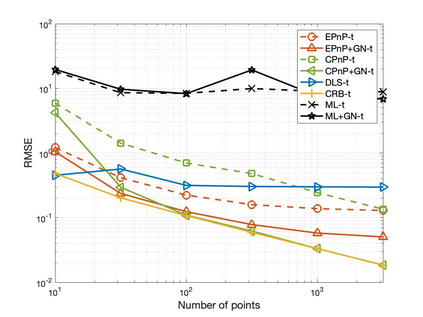
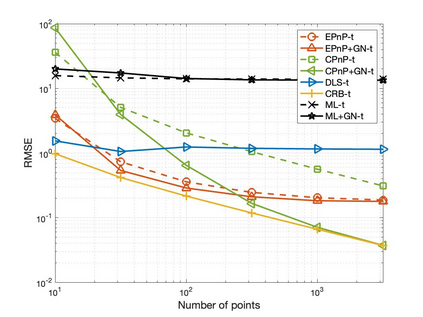
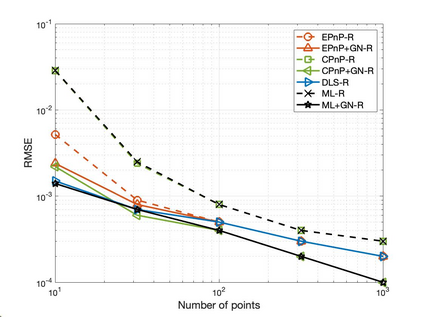
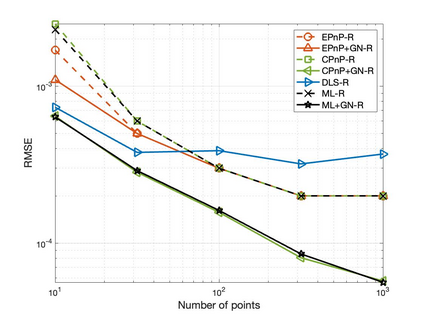
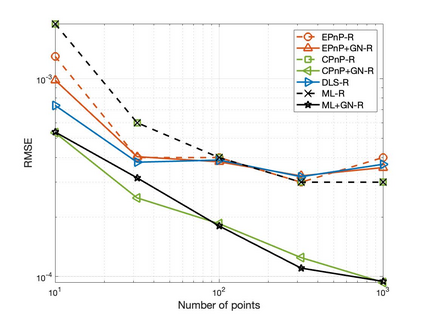
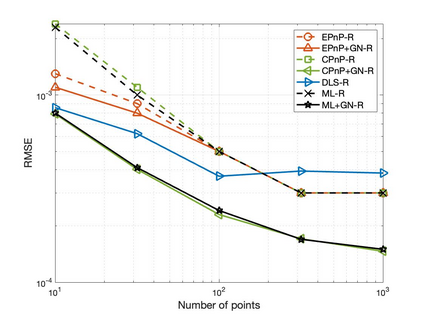
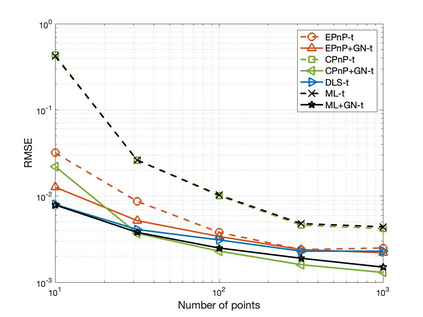
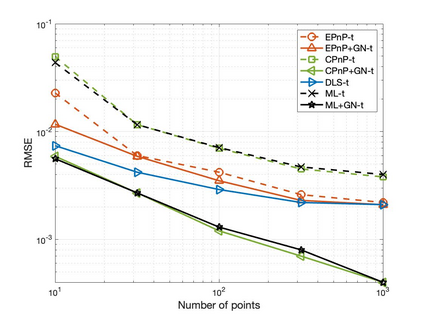
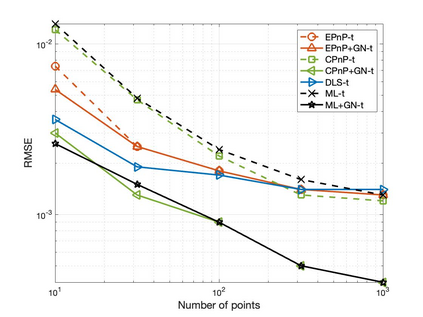
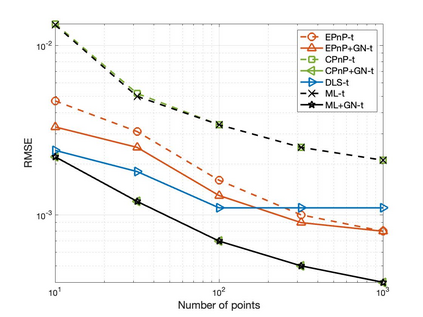
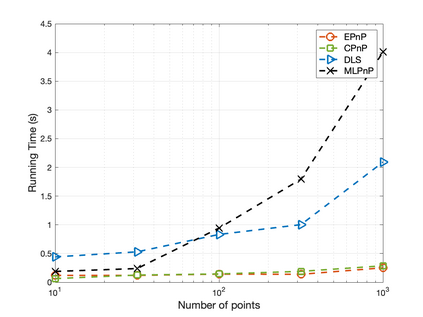
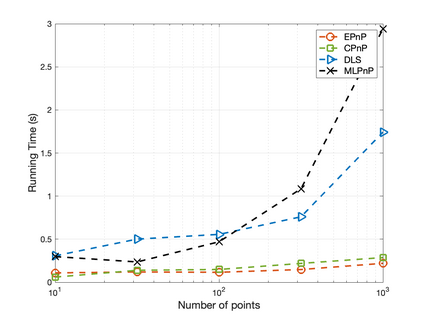
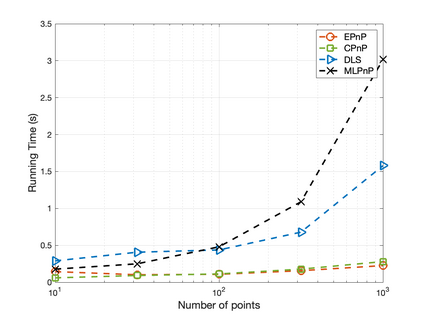
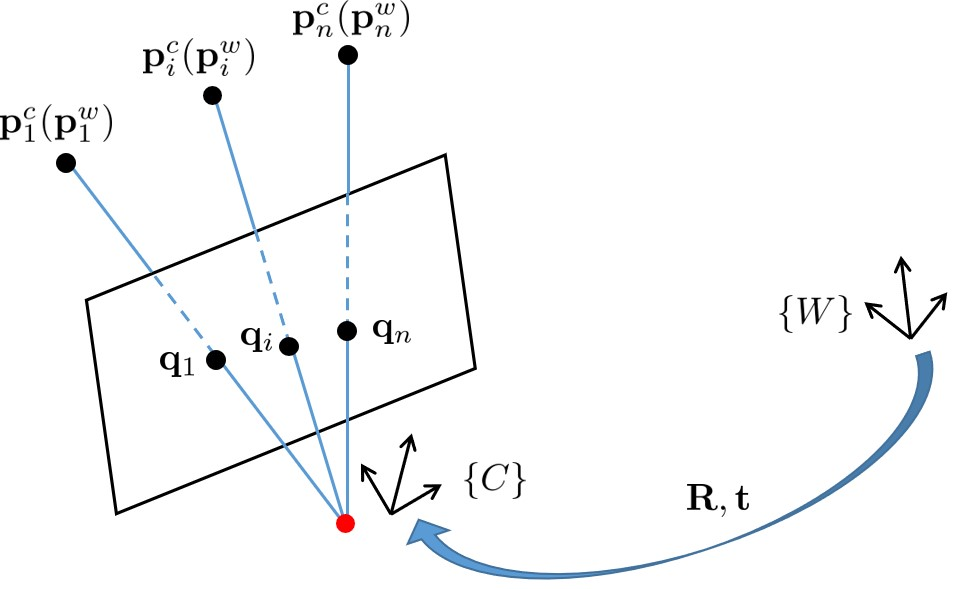
The Perspective-n-Point (PnP) problem has been widely studied in both computer vision and photogrammetry societies. With the development of feature extraction techniques, a large number of feature points might be available in a single shot. It is promising to devise a consistent estimator, i.e., the estimate can converge to the true camera pose as the number of points increases. To this end, we propose a consistent PnP solver, named \emph{CPnP}, with bias elimination. Specifically, linear equations are constructed from the original projection model via measurement model modification and variable elimination, based on which a closed-form least-squares solution is obtained. We then analyze and subtract the asymptotic bias of this solution, resulting in a consistent estimate. Additionally, Gauss-Newton (GN) iterations are executed to refine the consistent solution. Our proposed estimator is efficient in terms of computations -- it has $O(n)$ computational complexity. Experimental tests on both synthetic data and real images show that our proposed estimator is superior to some well-known ones for images with dense visual features, in terms of estimation precision and computing time.
翻译:视觉- 点( PnP) 问题已经在计算机视觉和摄影测量社会进行了广泛的研究。 随着地貌提取技术的发展, 大量的地貌点可以在一个镜头中找到。 很有希望设计一个一致的测算器, 也就是说, 估计可以随着点数的增加而归结到真实的摄像机表面。 为此, 我们提出一个一致的 PnP 求解器, 名为 emph{ CPnP}, 并消除偏差。 具体地说, 线性方程是通过测量模型的修改和变量的消除从原始投影模型中构建的, 通过测量模型的修改和变量的消除, 在此基础上, 可以获得一个封闭式的最小方位解决方案的解决方案。 我们然后分析并减去这个解决方案的无症状偏差, 从而得出一致的估测结果。 此外, 高斯- 纽顿( GN) 的校正是为了完善一致的解决方案。 我们提议的估测算器在计算方面是有效的 -- 它有美元( n) 的计算复杂性。 对合成数据和真实图像的实验测试表明, 我们提议的估测算器比一些精确的图像和精确的图像。