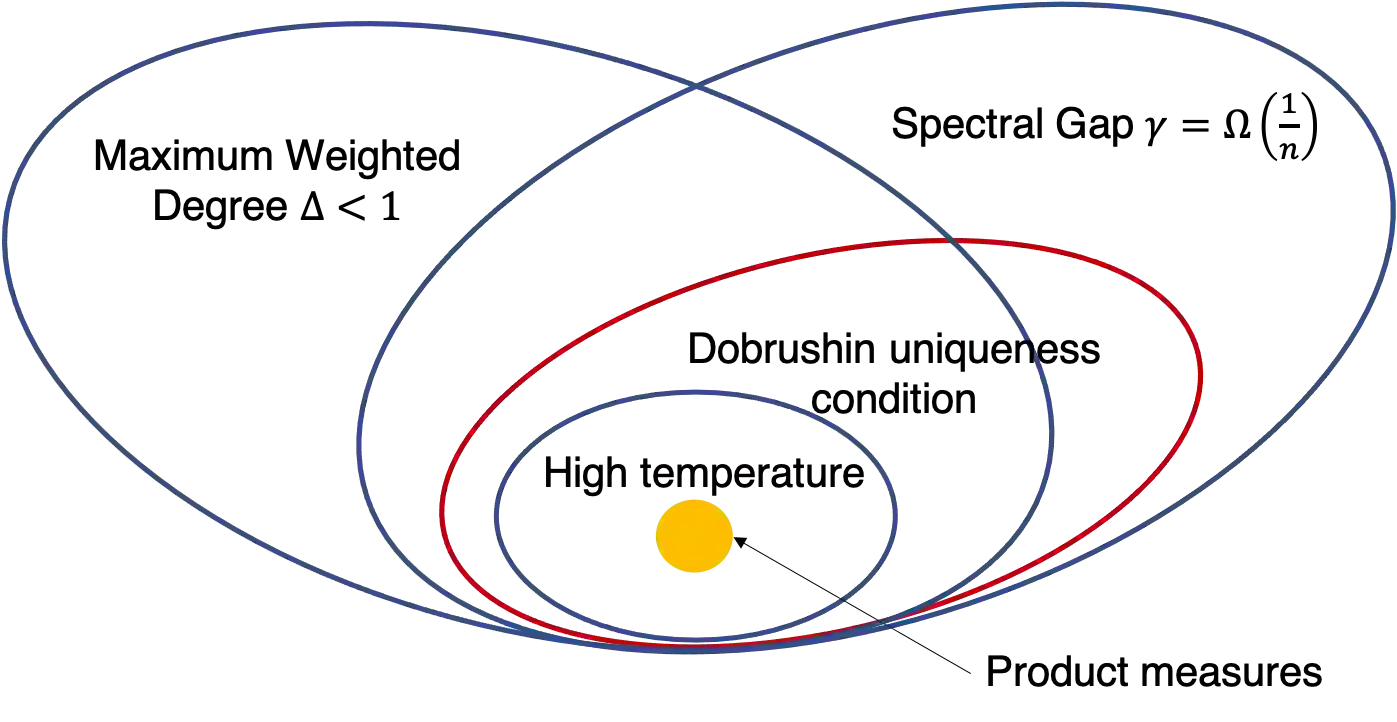
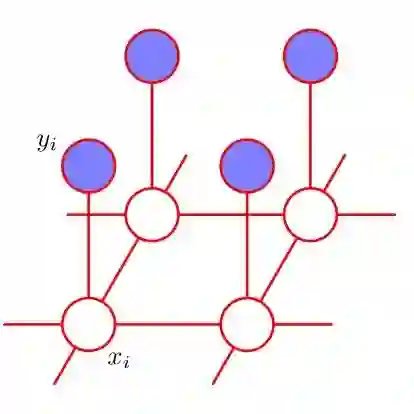
We study the problem of selling $n$ heterogeneous items to a single buyer, whose values for different items are dependent. Under arbitrary dependence, Hart and Nisan show that no simple mechanism can achieve a non-negligible fraction of the optimal revenue even with only two items. We consider the setting where the buyer's type is drawn from a correlated distribution that can be captured by a Markov Random Field, one of the most prominent frameworks for modeling high-dimensional distributions with structure. If the buyer's valuation is additive or unit-demand, we extend the result to all MRFs and show that max(SRev,BRev) can achieve an $\Omega\left(\frac{1}{e^{O(\Delta)}}\right)$-fraction of the optimal revenue, where $\Delta$ is a parameter of the MRF that is determined by how much the value of an item can be influenced by the values of the other items. We further show that the exponential dependence on $\Delta$ is unavoidable for our approach and a polynomial dependence on $\Delta$ is unavoidable for any approach. When the buyer has a XOS valuation, we show that max(Srev,Brev) achieves at least an $\Omega\left(\frac{1}{e^{O(\Delta)}+\frac{1}{\sqrt{n\gamma}}}\right)$-fraction of the optimal revenue, where $\gamma$ is the spectral gap of the Glauber dynamics of the MRF. Note that in the special case of independently distributed items, $\Delta=0$ and $\frac{1}{n\gamma}\leq 1$, and our results recover the known constant factor approximations for a XOS buyer. We further extend our parametric approximation to several other well-studied dependency measures such as the Dobrushin coefficient and the inverse temperature. Our results are based on the Duality-Framework by Cai et al. and a new concentration inequality for XOS functions over dependent random variables.
翻译:我们研究的是向单一买家出售美元混杂项目的问题,这些买家的不同项目的价值取决于X-limal {xqual {。在任意依赖性下,哈特和尼桑显示,任何简单的机制都无法达到最佳收入中一个不可忽略的部分,即使只有两个项目。我们考虑的是买方类型从相关分布中抽取,而该分布可以被一个Markov随机字段所捕捉,这是模拟高维分布结构的最突出的框架之一。如果买家的估价是添加或单位需求,那么我们将结果扩大到所有MRFs(SRev,BRev),并表明最大(S-limal-limal_$美元)能够达到美元Omerga\left(formax$_Octa$_Olight_right) 最佳收入中的美元部分。当我们买家能够以其他项目的价值为基点时,我们发现对美元-liferal-lideal1 Ormal1 的计算结果,当我们买家能够以一个不断的数值来计算。