Parallel Projection -- A New Return Mapping Algorithm for Finite Element Modeling of Shape Memory Alloys

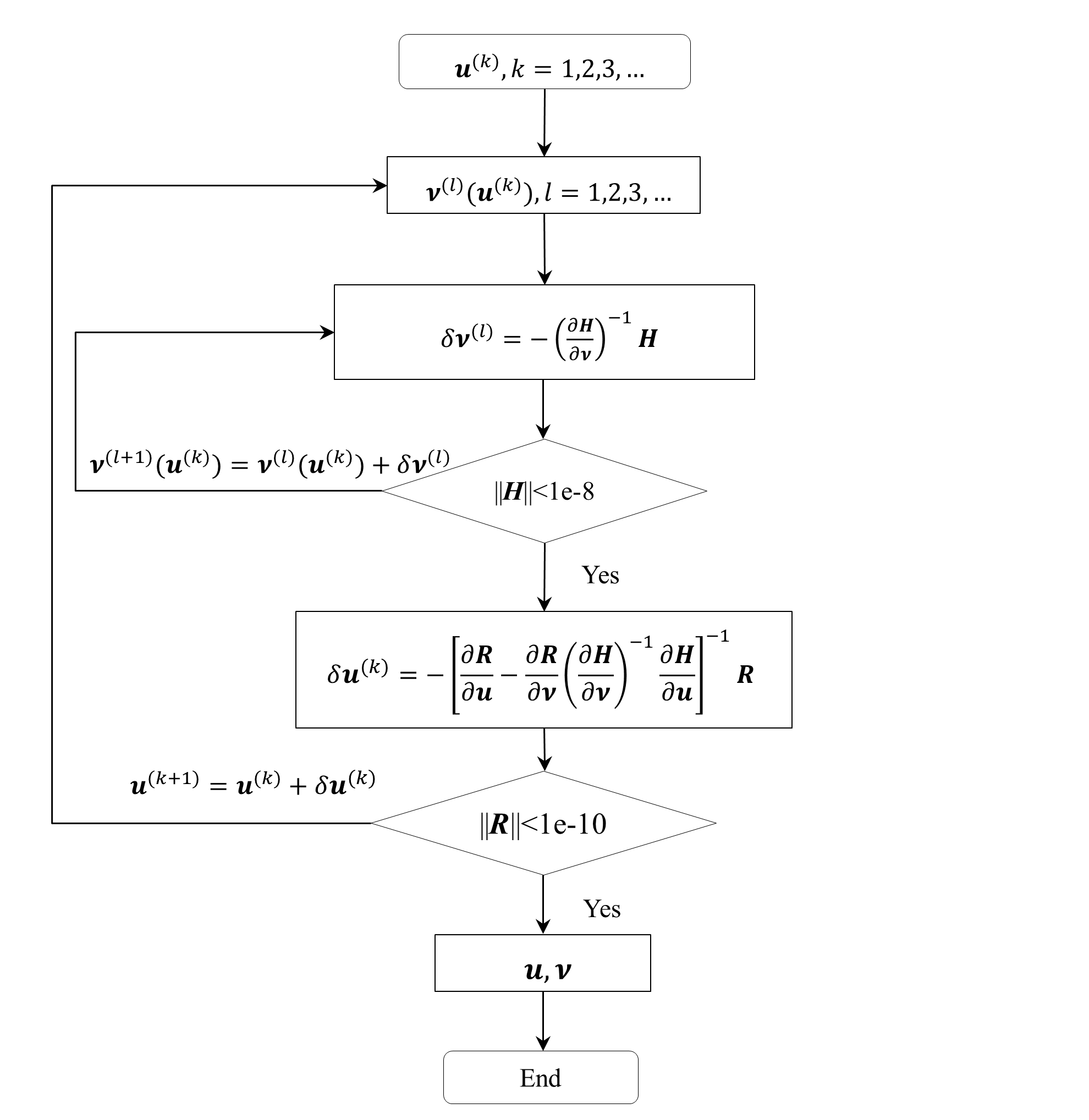
We present a novel method for finite element analysis of inelastic structures containing Shape Memory Alloys (SMAs). Phenomenological constitutive models for SMAs lead to material nonlinearities, that require substantial computational effort to resolve. Finite element analysis methods, which rely on Gauss quadrature integration schemes, must solve two sets of coupled differential equations: one at the global level and the other at the local, i.e. Gauss point level. In contrast to the conventional return mapping algorithm, which solves these two sets of coupled differential equations separately using a nested Newton procedure, we propose a scheme to solve the local and global differential equations simultaneously. In the process we also derive closed-form expressions used to update the internal state variables, and unify the popular closest-point and cutting plane methods with our formulas. Numerical testing indicates that our method allows for larger thermomechanical loading steps and provides increased computational efficiency, over the standard return mapping algorithm.