On the equivalence of holding cost and response time for evaluating performance of queues

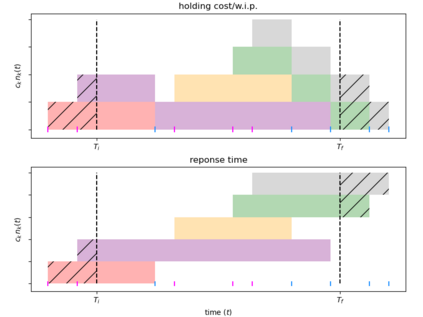
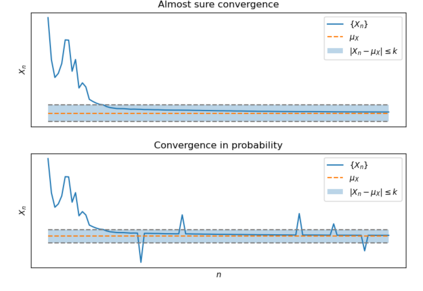
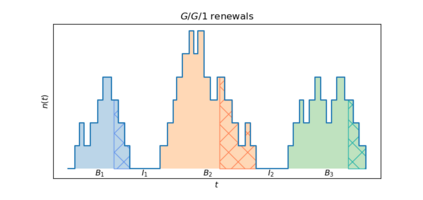
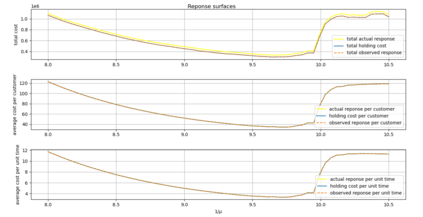
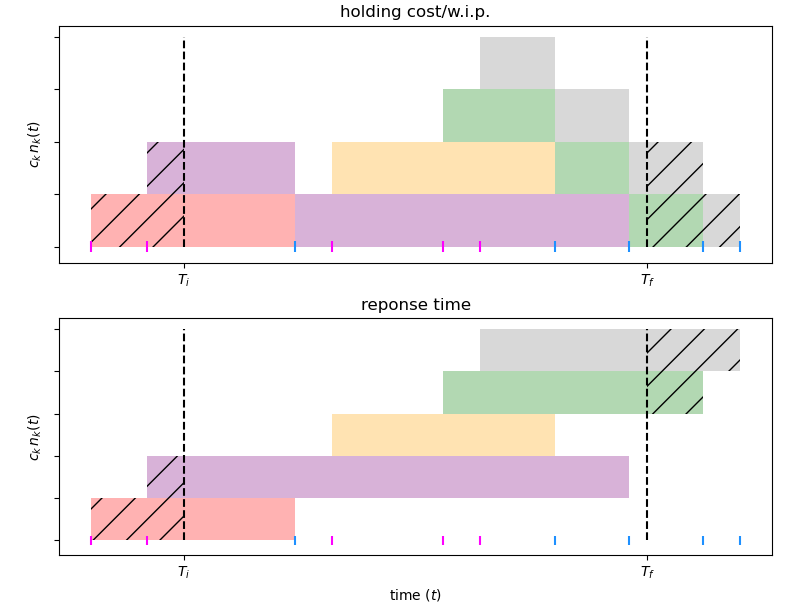
This self-contained discussion relates the long-run average holding cost per unit time to the long-run average response time per customer in a $G/G/1$ queue with no assumption made on the order of service. The only restriction established is that the system be ergodic. This is achieved using standard queuing theory. The practical relevance of such a result is discussed in the context of simulation output analysis as well as through an application to formulating a Markov Decision Process that minimises long-run average response time per customer.