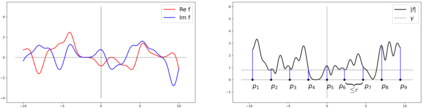
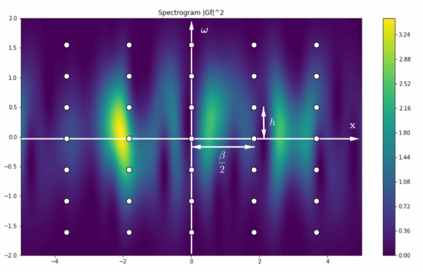
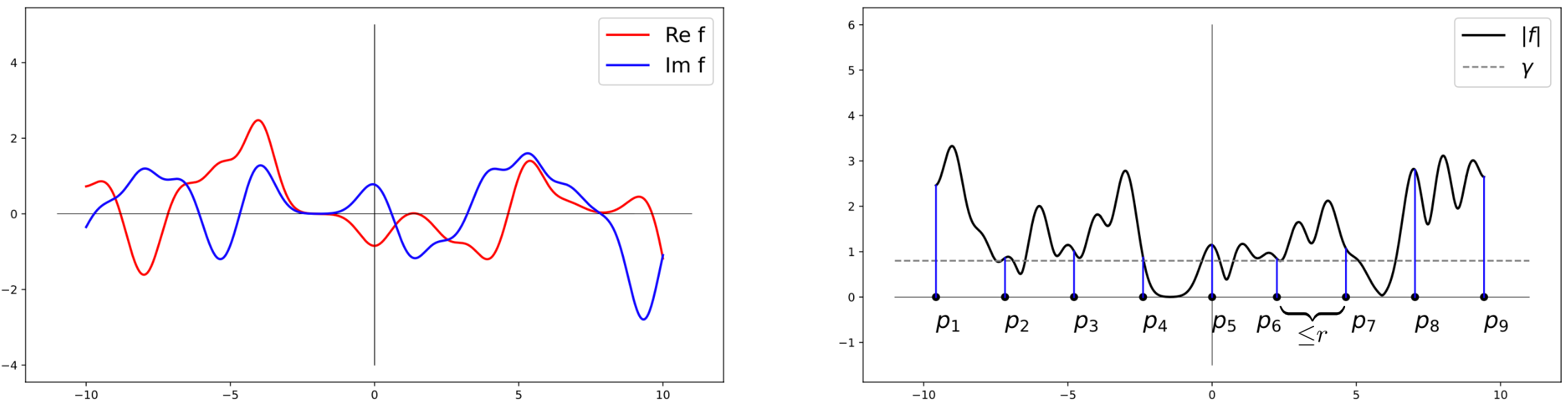
We study the phase reconstruction of signals $f$ belonging to complex Gaussian shift-invariant spaces $V^\infty(\varphi)$ from spectrogram measurements $|\mathcal{G}f(X)|$ where $\mathcal{G}$ is the Gabor transform and $X \subseteq \mathbb{R}^2$. An explicit reconstruction formula will demonstrate that such signals can be recovered from measurements located on parallel lines in the time-frequency plane by means of a Riesz basis expansion. Moreover, connectedness assumptions on $|f|$ result in stability estimates in the situation where one aims to reconstruct $f$ on compact intervals. Driven by a recent observation that signals in Gaussian shift-invariant spaces are determined by lattice measurements [Grohs, P., Liehr, L., Injectivity of Gabor phase retrieval from lattice measurements, arXiv:2008.07238] we prove a sampling result on the stable approximation from finitely many spectrogram samples. The resulting algorithm provides a non-iterative, provably stable and convergent approximation technique. In addition, it constitutes a method of approximating signals in function spaces beyond $V^\infty(\varphi)$, such as Paley-Wiener spaces.
翻译:我们研究的是来自光谱测量的属于复合高山变换空间的信号的分阶段重建(美元) 美元(瓦夫蒂) 美元(瓦夫蒂) 美元(瓦夫蒂) 美元(瓦夫菲) 美元(瓦夫菲) 美元(瓦夫菲) 美元(瓦夫菲) 美元(瓦什卡) 美元(瓦什卡) 美元(瓦什卡) 美元(瓦什卡) 美元(瓦什卡) 美元(瓦什卡) 美元(瓦什卡) 美元(美元) 的信号是加博的变换和 美元(Gabor) 美元 (Gabor, P., Liehr, L.) 。 明确的重建公式将表明,通过扩大Rieszyzy 基础,从位于时频平面平线上的测量线上的测量中可以恢复这些信号。 此外,对美元(美元) 的连接假设导致一个稳定的估算结果, 由此得出的算算法提供了一种不固定的、 稳定和稳定的方法。