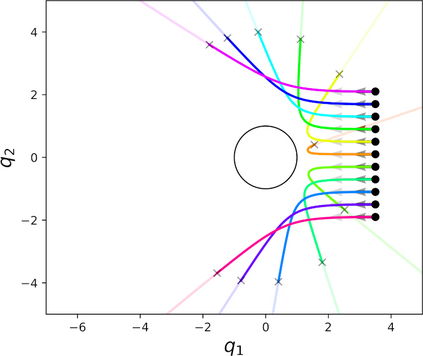
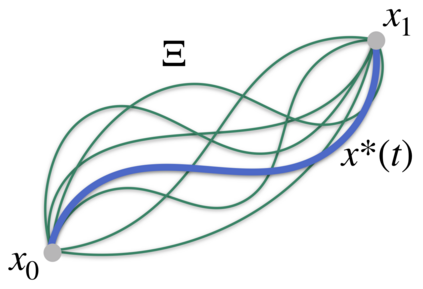
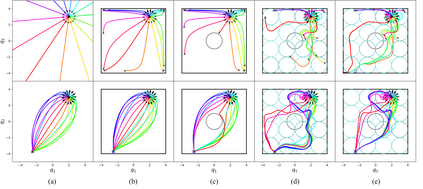
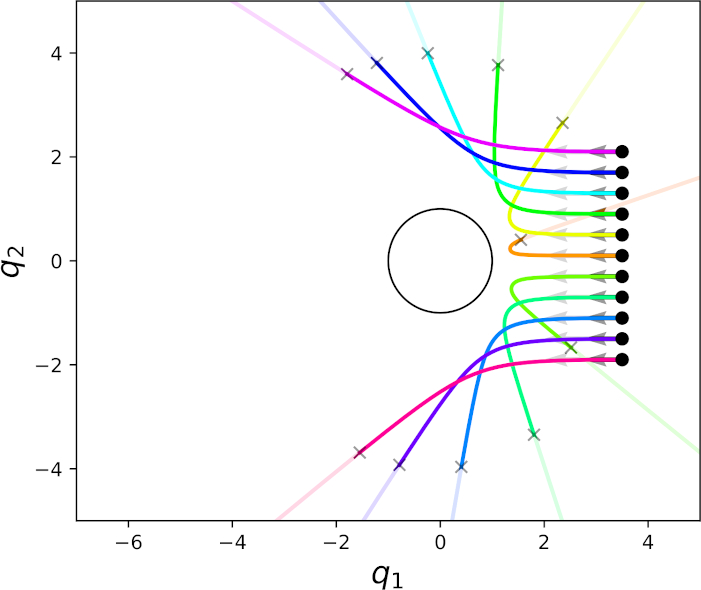
Robotics research has found numerous important applications of Riemannian geometry. Despite that, the concept remain challenging to many roboticists because the background material is complex and strikingly foreign. Beyond {\em Riemannian} geometry, there are many natural generalizations in the mathematical literature -- areas such as Finsler geometry and spray geometry -- but those generalizations are largely inaccessible, and as a result there remain few applications within robotics. This paper presents a re-derivation of spray and Finsler geometries we found critical for the development of our recent work on a powerful behavioral design tool we call geometric fabrics. These derivations build from basic tools in advanced calculus and the calculus of variations making them more accessible to a robotics audience than standard presentations. We focus on the pragmatic and calculable results, avoiding the use of tensor notation to appeal to a broader audience, emphasizing geometric path consistency over ideas around connections and curvature. We hope that these derivations will contribute to an increased understanding of generalized nonlinear, and even classical Riemannian, geometry within the robotics community and inspire future research into new applications.
翻译:机器人研究发现,里曼尼的几何有许多重要的应用。 尽管如此, 这一概念对许多机器人学家来说仍然具有挑战性, 因为背景材料复杂而惊人。 在叶利曼伊的几何学之外, 数学文献中有许多自然的概括性 -- -- 比如芬斯勒的几何学和喷雾几何学 -- -- 但是这些概括性基本数据基本上无法获得, 结果机器人内部仍然很少应用。 本文展示了喷雾和芬斯勒的几何学, 我们发现这对我们最近关于一个强大的行为设计工具的工作的发展至关重要, 我们称之为几何结构。 这些衍生数据来自高级微积分和变异学的基本工具, 使得机器人更便于阅读, 而不是标准演示。 我们侧重于务实和可计算的结果, 避免使用微调来吸引更广大的观众, 强调在连接和曲线上的各种想法的几何分解路径一致性。 我们希望这些衍生数据将有助于加深对一般非线性的理解, 甚至是典型的里伊曼、 几何测量学在机器人界内的新研究应用的启发性。