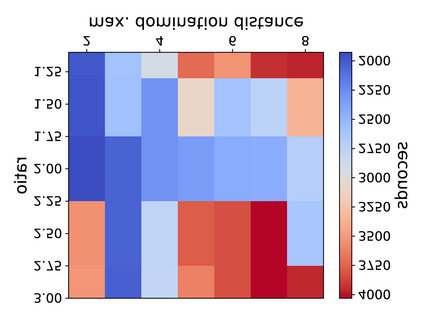
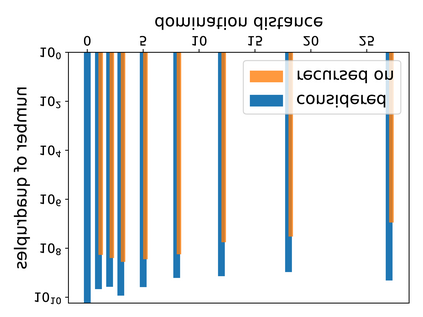
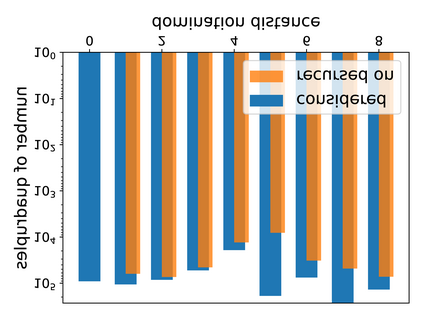
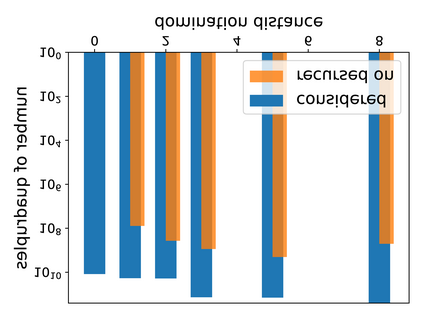
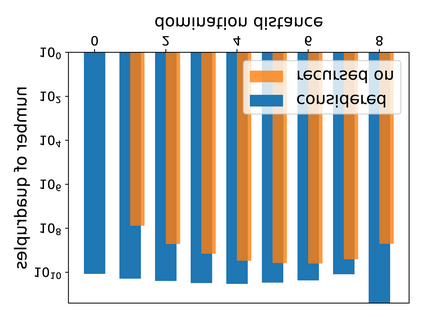
Hyperbolicity Computation through Dominating Sets *

Hyperbolicity is a graph parameter related to how much a graph resembles a tree with respect to distances. Its computation is challenging as the main approaches consist in scanning all quadruples of the graph or using fast matrix multiplication as building block, both are not practical for large graphs. In this paper, we propose and evaluate an approach that uses a hierarchy of distance-k dominating sets to reduce the search space. This technique, compared to the previous best practical algorithms, enables us to compute the hyperbolicity of graphs with unprecedented size (up to a million nodes) and speeds up the computation of previously attainable graphs by up to 3 orders of magnitude while reducing the memory consumption by up to more than a factor of 23.