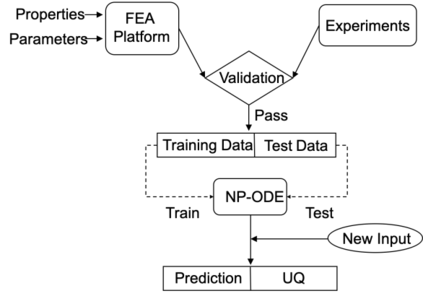
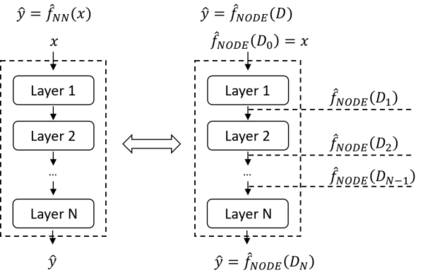
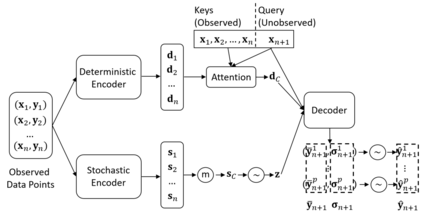
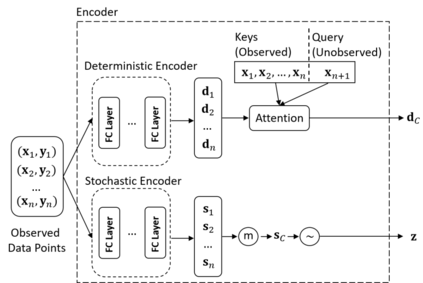
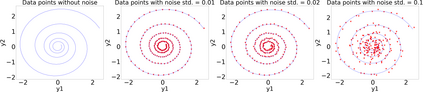
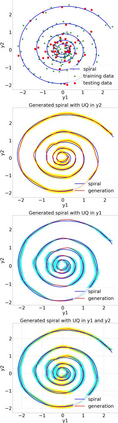
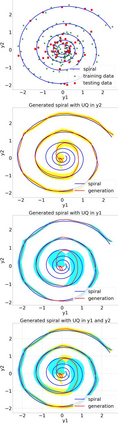
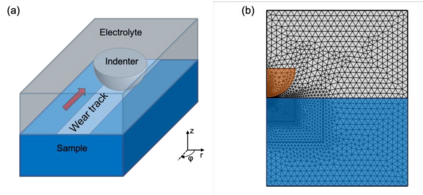
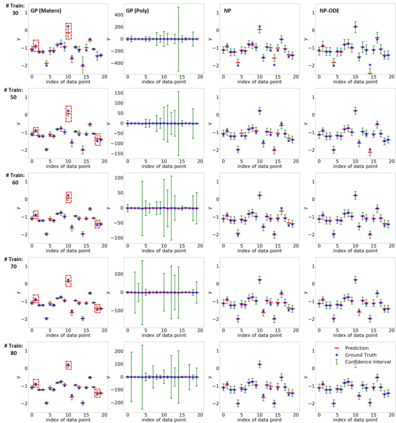
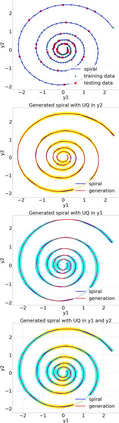
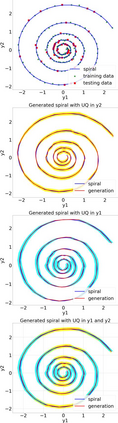
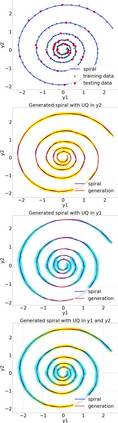
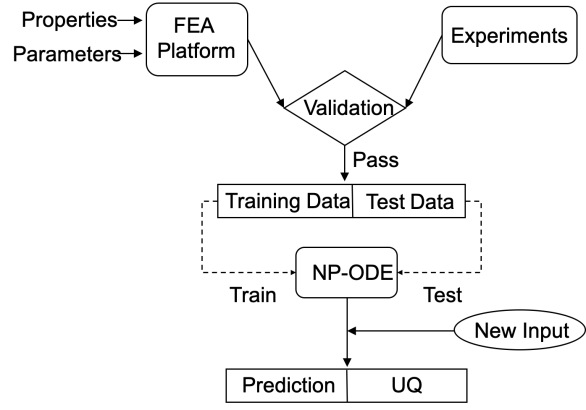
Finite element analysis (FEA) has been widely used to generate simulations of complex and nonlinear systems. Despite its strength and accuracy, the limitations of FEA can be summarized into two aspects: a) running high-fidelity FEA often requires significant computational cost and consumes a large amount of time; b) FEA is a deterministic method that is insufficient for uncertainty quantification (UQ) when modeling complex systems with various types of uncertainties. In this paper, a physics-informed data-driven surrogate model, named Neural Process Aided Ordinary Differential Equation (NP-ODE), is proposed to model the FEA simulations and capture both input and output uncertainties. To validate the advantages of the proposed NP-ODE, we conduct experiments on both the simulation data generated from a given ordinary differential equation and the data collected from a real FEA platform for tribocorrosion. The performances of the proposed NP-ODE and several benchmark methods are compared. The results show that the proposed NP-ODE outperforms benchmark methods. The NP-ODE method realizes the smallest predictive error as well as generates the most reasonable confidence interval having the best coverage on testing data points.
翻译:微量元素分析(FEA)已被广泛用于模拟复杂和非线性系统,尽管其强度和准确性,但FEA的局限性可以归纳为两个方面:(a) 高不贞度FEA的运行往往需要大量的计算成本并耗费大量的时间;(b) FEA是一种确定性方法,在模拟具有各种不确定因素的复杂系统时,这种方法不足以确定不确定性的量化(UQ)方法;在本文件中,以物理为根据的数据驱动替代模型,名为Neal Procised Aided Pal difficult Equalation(NP-ODE),建议模拟FEA模拟并捕捉投入和产出不确定性。为了验证拟议的PODE的优点,我们对从一个给定的普通差异方程式产生的模拟数据以及从一个实际FEA平台收集的数据进行实验,用以模拟三重孔分解。比较了拟议的NP-ODE和若干基准方法的绩效。结果显示,拟议的NP-ODE优于模版基准方法。