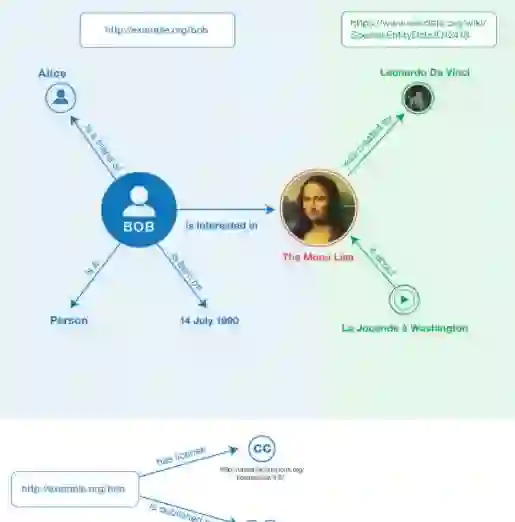
Property graphs constitute data models for representing knowledge graphs. They allow for the convenient representation of facts, including facts about facts, represented by triples in subject or object position of other triples. Knowledge graphs such as Wikidata are created by a diversity of contributors and a range of sources leaving them prone to two types of errors. The first type of error, falsity of facts, is addressed by property graphs through the representation of provenance and validity, making triples occur as first-order objects in subject position of metadata triples. The second type of error, violation of domain constraints, has not been addressed with regard to property graphs so far. In RDF representations, this error can be addressed by shape languages such as SHACL or ShEx, which allow for checking whether graphs are valid with respect to a set of domain constraints. Borrowing ideas from the syntax and semantics definitions of SHACL, we design a shape language for property graphs, ProGS, which allows for formulating shape constraints on property graphs including their specific constructs, such as edges with identities and key-value annotations to both nodes and edges. We define a formal semantics of ProGS, investigate the resulting complexity of validating property graphs against sets of ProGS shapes, compare with corresponding results for SHACL, and implement a prototypical validator that utilizes answer set programming.
翻译:属性图是显示知识图的数据模型。 它们允许方便地陈述事实, 包括事实事实的事实, 由其他三重主题或对象位置的三重代表。 维基数据等知识图是由多种贡献者和一系列来源创建的, 使得它们容易出现两种类型的错误。 第一类错误, 即事实的虚假, 由属性图通过源代码和有效性的表示处理, 使三重数据作为主元数据位置的一阶对象出现。 第二种错误, 即违反域限制, 至今尚未在属性图中得到解决。 在 RDF 演示中, 可以通过形状语言, 如 SHACL 或 ShEx 来处理这一错误, 从而能够检查图表是否适用于一系列域限制。 借用 SHACL 的语法和语义定义, 我们为属性图设计一种形状语言, ProGS, 能够对属性图作形状约束, 包括它们的具体构造, 例如与身份和关键值注释的边缘, 到节点和边缘。 在 RDFDF 演示中, 我们用一个格式的形状来测量结果, 。